Поурочные разработки по геометрии 10 класс
Разложение вектора по трем некомпланарным векторам - КОМПЛАНАРНЫЕ ВЕКТОРЫ - ВЕКТОРЫ В ПРОСТРАНСТВЕ
Цель урока:
- рассмотреть теорему о разложении вектора по трем некомпланарным векторам.
Ход урока
I. Организационный момент
II. Коллективная проверка домашнего задания.
III. Опрос
У доски - 2 ученика (1-й отвечает сразу, 2-й готовится)
1. ученик - компланарные векторы и правило параллелепипеда.
2. ученик - доказать признак компланарности 3-х векторов.
3. ученик - задача № 362.
Дано: ABCD - тетраэдр; ВК = КС. DK разложить по ![]() (рис. 1).
(рис. 1).
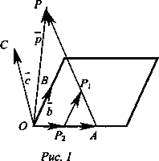
Решение: К - середина; ![]()
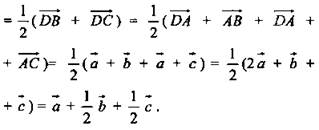
IV. Объяснение нового материала
Если вектор ![]() представлен в виде (1)
представлен в виде (1) ![]() где х, у, z - некоторые числа, то говорят что вектор
где х, у, z - некоторые числа, то говорят что вектор ![]() разложен по векторам
разложен по векторам ![]()
![]() Числа х, у, z называются коэффициент разложения. Теорема: Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициент разложения определяется единственным образом.
Числа х, у, z называются коэффициент разложения. Теорема: Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициент разложения определяется единственным образом.
Доказательство: Пусть ![]() - данные некомпланарные вектора
- данные некомпланарные вектора ![]()
![]() Отметим произвольную точку О и отложим от нее векторы (2);
Отметим произвольную точку О и отложим от нее векторы (2); ![]() Через т. Р проведем прямую параллельную ОС. Р1 = с ∩ АОВ (если Р ∈ ОС, то в качестве Р1 возможен т. О). Через Р1 проведем Р1Р2 параллельную ОВ; Р2 = с ∩ ОА (если Р1 ∈ ОВ то в качестве Р2 возьмем точку О);
Через т. Р проведем прямую параллельную ОС. Р1 = с ∩ АОВ (если Р ∈ ОС, то в качестве Р1 возможен т. О). Через Р1 проведем Р1Р2 параллельную ОВ; Р2 = с ∩ ОА (если Р1 ∈ ОВ то в качестве Р2 возьмем точку О); ![]() (3). Векторы
(3). Векторы ![]()
![]() коллинеарные, поэтому существуют числа х, у, z такие, что
коллинеарные, поэтому существуют числа х, у, z такие, что ![]()
![]() подставляя в (3) получим:
подставляя в (3) получим: ![]()
![]() учитывая (2) получаем
учитывая (2) получаем ![]()
Докажем единственность коэффициентов разложения. Допустим, что имеется ещё одно разложение вектора ![]() Вычитая это равенство из (1), получим
Вычитая это равенство из (1), получим ![]()
![]() Это равенство выполняется только тогда, когда х – х1 = 0, у – у1 = 0, z – z1 = 0. Если предположить, например, что z – z1 ≠ 0, то из этого равенства получим
Это равенство выполняется только тогда, когда х – х1 = 0, у – у1 = 0, z – z1 = 0. Если предположить, например, что z – z1 ≠ 0, то из этого равенства получим ![]() следовательно, векторы
следовательно, векторы ![]() - компланарны (это противоречит условию теоремы).
- компланарны (это противоречит условию теоремы).
Значит, наше предположение неверно, х = х1, у = у1, z = z1. Следовательно, коэффициенты разложения определяются единственным образом.
V. Формирование знаний и умений
У доски: № 361. Дано: ABCDA1B1C1D1 параллелепипед; О - точка пересечения диагоналей. Разложить ![]() по векторам;
по векторам; ![]() (рис. 2).
(рис. 2).
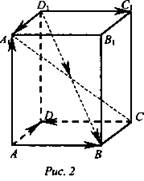
Решение: ![]()
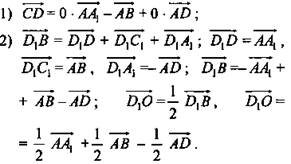
№ 363. Дано: ABCD - параллелограмм, M ![]() (рис. 3)
(рис. 3)
Разложить ![]()
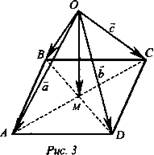
Решение: ![]()
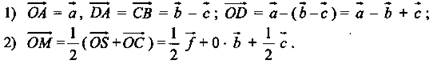
№ 366. М - точка пересечения медиан, О произвольная точка пространства (рис. 4).
Доказать: ![]()
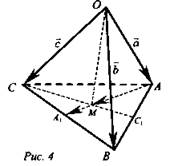
Решение: Пусть ![]()

![]()
VI. Подведение итогов
Домашнее задание
П. 41 № 362, 364, дополнительно № 365, 362. Решение в учебнике (1 способ).
№ 364
![]()
№ 365
![]()