Поурочные разработки по геометрии 10 класс
Призма. Площадь поверхности призмы - ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА - МНОГОГРАННИКИ
Цели урока:
1) рассмотреть виды призмы, ввести понятие площади поверхности призмы;
2) вывести формулу для вычисления площади поверхности прямой призмы.
Ход урока
I. Проверка домашнего задания
Индивидуальный и фронтальный опрос
Двое у доски записывают решение домашних номеров. № 220 и № 295 (а, б) и третий № 295 (в, г). Двое учеников решают задачи по карточкам индивидуального опроса.
Карточка 1 (для среднего ученика).
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед. АВ = 4, АА1 = 6, А1С = √56.
Найдите: AD.
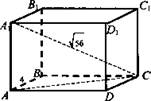
Решение: ![]()
![]() (Ответ: 2.)
(Ответ: 2.)
Карточка 2 (для сильного ученика.
Дано: ABCA1B1C1 - прямая треугольная призма: АС = ВС = 5, АВ = 6, ВD ⊥ АС ∠BCD = 30°.
Найдите: cos C1BC.
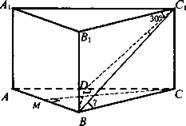
Решение: В ΔАВС: ![]()
![]() так как
так как ![]()
![]() так как ΔСС1В прямоугольный -
так как ΔСС1В прямоугольный - ![]() (Ответ: 25/48.)
(Ответ: 25/48.)
С остальными учащимися проводится устный опрос.
1. Среди изображенных тел выберите те, которые являются многогранниками.
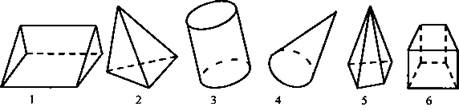
(Ответ: 1, 2, 5, 6.)
2. Какие из них являются призмами?
(Ответ: 1 и 6 (рисунки оставить на доске и распределить между вариантами)).
3. Обозначьте и назовите для призмы:
а) вершины; .
б) основания: .
в) боковые грани;
д) противоположные грани;
е) диагонали грани;
ж) диагонали призмы.
4. Закончите предложения:
1) Высотой призмы называется ...
2) Диагональю призмы называется...
3) Диагональным сечением призмы называется сечение плоскостью, проходящей через ...
4) Параллелепипедом называется ...
5) Прямоугольным параллелепипедом называется ...
6) Кубом называется прямоугольный параллелепипед, у которого ...
7) Примером моделей призмы и параллелепипеда из реальной жизни является ...
5. Ответьте на вопросы:
1) Какие многогранники лежат в основании призмы?
2) В каких плоскостях лежат основания призмы?
3) Какими отрезками являются боковые ребра призмы?
4) Что представляет собой диагональное сечение призмы?
5) Какими многоугольниками являются все грани параллелепипеда (любого)?
6) Какими фигурами являются все грани прямоугольного параллелепипеда?
7) Сколько измерений у прямоугольного параллелепипеда?
8) Почему все высоты призмы равны между собой?
9) Какие многоугольники являются основаниями и боковой гранью треугольной призмы (четырехугольной и пятиугольной)?
10) Сколько диагоналей у треугольной (четырехугольной, пятиугольной) призм?
11) Призма имеет 30 граней. Какой многогранник лежит в ее основании? Сколько вершин и ребер?
II. Объяснение нового материала
Вопрос: Покажите различие многоугольников, из которых состоит произвольный параллелепипед и правильный параллелепипед.
Ответ: Произвольный состоит из параллелограммов, а прямоугольный из прямоугольников.
Вывод: У произвольного параллелепипеда боковые ребра не перпендикулярны основанию, а у прямоугольного - перпендикулярны.
Так же и у призмы (можно показать с помощью «воздушной» модели, примеры прямой и наклонной призм), п. 27 (продолжение).
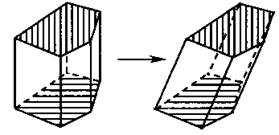
Составим схему:
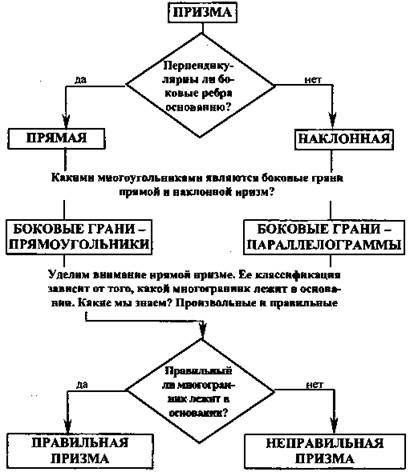
Устно № 218
Решение: а) У прямой призмы боковые ребра перпендикулярны к основаниям, а основания - параллельны, следовательно, боковые грани - прямоугольники. б) Основания - правильные многогранники. Боковые ребра равны, боковые грани - равные прямоугольники.
Далее ввести понятие боковой поверхности, полной поверхности призмы (п. 27). Можно использовать развертки призм, например, треугольная.
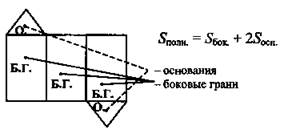
Докажем теорему о площади боковой поверхности прямой призмы.
Теорема (п. 27)
Дано: Прямая n-угольная призма; пусть а1, a2, ..., аn - стороны, h - высота.
Доказать: ![]()
Доказательство: Так как боковыми гранями прямой призмы являются прямоугольники, то площадь боковой поверхности равна сумме площадей указанных прямоугольников.

Теорема доказана.
Составим таблицу и приведем в ней данные для вычисления Sбок.; Sосн.; Sполн..
Правильная призма |
Sбок. |
Sосн. |
Sполн. |
Треугольная призма |
3ah |
|
|
Четырехугольная призма |
4ah |
a2 |
2a(h + а) |
Шестиугольная призма |
6ah |
|
|
III. Применение званий в стандартной ситуаци.
1. № 229 а
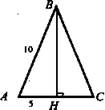
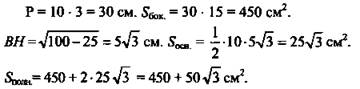
(Ответ: 450 см2 и 450 + 50√3 см2.)
2. № 230. Дано: ABCA1B1C1 - прямая призма, АВ = 5 см, ВС = 3 см, ∠ABC = 120°. Наибольшая из боковых площадей граней 35 см2.
Найти: Sбок.
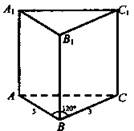
Решение:
1) Из ΔАВС ![]()
![]()
2) АС - большее ребро основания, значит, АА1С1С имеет большую площадь. ![]()
![]()
![]() (Ответ: 75 см2.)
(Ответ: 75 см2.)
IV. Подведение итогов
Домашнее задание
П. 27; вопросы 3-8 к главе III.
№ 229 (б, в)
б) В основании - квадрат. Sосн. = а42; а4 - сторона квадрата. ![]()
![]() (Ответ: 672 дм2.)
(Ответ: 672 дм2.)
в) В основании - правильный 6-угольник. ![]() а6 - сторона шестиугольника.
а6 - сторона шестиугольника. ![]()
![]() (Ответ: 97 дм2.)
(Ответ: 97 дм2.)
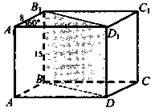
№ 231
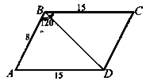
Решение: Пусть АВ1 = 8 см, A1D1 = 15 см, ∠B1A1D = 60°. Пусть боковое ребро равно Н, тогда площадь первого диагонального сечения ![]() а площадь второго
а площадь второго ![]()
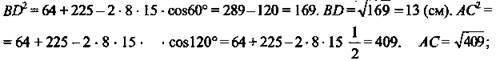
![]() поэтому АС > BD. Наименьшее сечение BB1D1D. Сечение изображено на рисунке,
поэтому АС > BD. Наименьшее сечение BB1D1D. Сечение изображено на рисунке, ![]()

(Ответ: ![]() )
)