Поурочные разработки по геометрии 10 класс
Решение задач - ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) подготовить учащихся к зачету;
2) решить задачи, близкие по содержанию задачам, включенным в зачет.
Ход урока
I. Проверка домашнего задания
Двое учеников решают у доски домашние задачи.
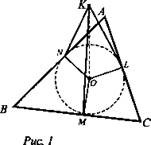
№ 203. Дано: О - центр окружности, вписанной в ΔАВС; OK ⊥ ABC, АВ = ВС = 10 см, АС = 12 см, ОК = 4 см (рис. 1).
Найти: расстояние от точки К до сторон ΔАВС.
Решение:
1. Окружность касается сторон ΔАВС в точках N, L, М. NO = LO = МО = r, OK ⊥ ABC (по условию); ON ⊥ АВ; KN ⊥ AB; OL ⊥ AC ⇒ KL ⊥ АС; ОМ ⊥ ВС; КМ ⊥ ВС по теореме о 3-х перпендикулярах ⇒ NK, LK, МК - искомые отрезки.
2. Проекции этих отрезков равны радиусу вписанной окружности ⇒ равны и сами отрезки КМ = KL = KN.
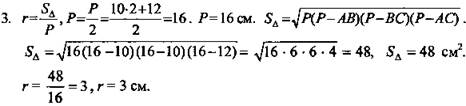
4. В ΔКОМ - прямоугольном - ![]() КМ = 5 см. (Ответ: 5 см.)
КМ = 5 см. (Ответ: 5 см.)
№ 207. Дано: ΔАВС, АС = 10 см, АВ = ВС = 13 см; КМ = MN = МР = ![]()
Найти: МО.
Решение:
1. О - центр вписанной окружности.
2. ΔМКО = ΔMNO = ΔМРО (по катету и гипотенузе).
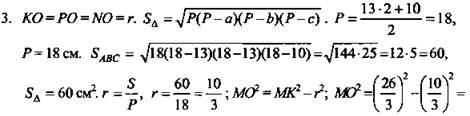
![]() (Ответ: 8 см.)
(Ответ: 8 см.)
II. Решение задач
Третий ученик решает задачу № 216.
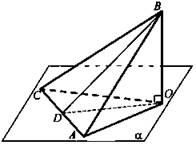
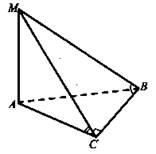
Дано: A ⊂ MN, В ⊂ MN; MN - ребро двугранного угла; ∠САК = 120°; АС ⊥ MN, BD ⊥ MN; AB = AC = BD = a (рис. 2).
Найти: CD.
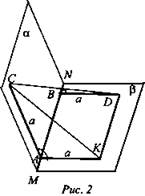
Решение:
1. Проведем DK || AB AK || BD, тогда АК ⊥ АВ, АК = KD = а. Так как АС ⊥ АВ; АК ⊥ АВ, то ∠CAK - линейный угол двугранного угла.
2. Из ΔСАК по теореме косинусов получим.
![]()
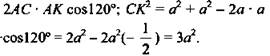
3. Так как АВ ⊥ САК; DK || АВ, то DK ⊥ САК ⇒ DK ⊥ СК, поэтому ΔCKD - прямоугольный. Из ΔCKD получим ![]()
![]() (Ответ: 2a.)
(Ответ: 2a.)
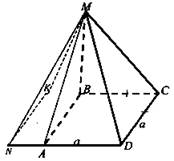
№ 204. Дано: ΔАВС - правильный; ОМ ⊥ ABC, ОМ = а; О ⊂ (ОМ), ∠MCO = φ (рис. 3).
Найти: а) МА, MB, МС, расстояние от точки М до прямых АВ, ВС, СА; б) l; в) SΔABC.
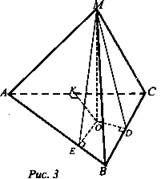
Решение:
а) 1. Проведем высоты AD, ВК, СЕ. В ΔABC они пересекаются в точке О (центр ΔАВС); ОА = ОВ = ОС; ΔМАО = ΔМВО = ΔМСО (по двум катетам) ⇒ МА = MB = МС.
2. Из ΔМСО имеем: ![]()
3. ![]() (по 2-м катетам) ⇒ МК = ME = MD.
(по 2-м катетам) ⇒ МК = ME = MD.
4. Так как OD - проекция MD на плоскость ABC и OD ⊥ ВС, то MD ⊥ ВС (теорема о 3-х перпендикулярах). Из ΔMDO:
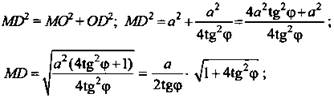
 (Ответ:
(Ответ: ![]() .
.
Провести разноуровневую самостоятельную работу на 6 вариантов.
Самостоятельная работа
I уровень |
|
Вариант I |
Вариант II |
В прямоугольном параллелепипеде измерения равны 6, 8, 10. Найти диагональ параллелепипеда и угол между диагональю параллелепипеда и плоскостью его основания.
|
В прямоугольном параллелепипеде измерения равны 5, 7, √47. Найти диагональ параллелепипеда и синус угла между диагональю параллелепипеда и плоскостью его основания.
|
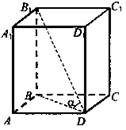
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед, АВ = 6, AD = 8, AA1 = 10. Найти: 1 .B1D; 2. ∠B1DB. Решение:
(Ответ: 10√2; 45°.) |
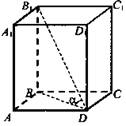
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; АВ = 5, AD = √47; AA1 = 7. Найти: 1. B1D; 2. sin a. Решение:
(Ответ: 11; 7/11.) |
II уровень |
|
Вариант III |
Вариант IV |
Из вершины A прямоугольного ΔАВС (∠C = 90°, ∠B = 60°) восстановлен перпендикуляр к плоскости ABC и на нем взят отрезок AM = h. Точка М соединена с В и С. Найдите SΔMBC, если двугранный ∠ABCM = 30°.
Дано: ΔАВС - прямоугольный, ∠С = 90°, ∠В = 60°; AM ⊥ ABC, АМ = h; ∠АВСМ = 30°. Найти: SΔABC. Решение: 1. МА ⊥ АBС; АС ⊥ ВС, то по теореме о 3-х перпендикулярах МС ⊥ ВС ⇒ двугранным углом между плоскостями ВСМ и ABC будет ∠АСМ. 2. ΔАМС - прямоугольный; 3. ΔABC - прямоугольный; 4. |
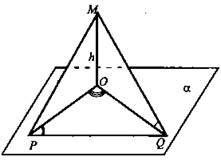
Точка М находится на расстоянии h от плоскости α. Проведены 2 наклонные МР и MQ (где Р и Q - основания наклонных), соответственно под углами 45° и 60°. Найдите PQ, если ∠POQ = 150°, где О - основание перпендикуляра МО, МО ⊥ α.
Дано: МР и MQ - наклонные; МО = h; ∠MQO = 45°; ∠МРО = 60°; ∠POQ = 150°; M ⊄ α. Найти: PQ. Решение:
|
III уровень |
|
Вариант V |
Вариант VI |
Треугольник AВС равносторонний, сторона АВ наклонена под ∠45° к плоскости α. Под каким углом наклонена плоскость ΔABC к плоскости α.
Дано: ΔАВС – равносторонний, ∠ВАО = 45°; АС ⊂ α. Найти: ∠BDO. Решение: 1. Проведем BD ⊥ АС и ВО ⊥ α. По теореме о 3-х перпендикулярах OD ⊥ АС, BD ⊥ AC => АС ⊥ BOD; ∠BDO – линейный угол двугранного угла ВАСО, угол между плоскостью α и плоскостью ΔABC. 2. ΔАВО - прямоугольный (ВО ⊥ α), следовательно ВО ⊥ АО. По определению перпендикуляра к плоскости; ВО = АО = а. 3. АВ = а√2 (т. Пифагора). 4. ΔABC - прямоугольный; 5. ΔDBO - прямоугольный; |
Плоскость квадрата ABCD со стороной а перпендикулярна плоскости равнобедренного ΔВСМ с углом В 120°. Найдите SΔADM.
Дано: ABCD - квадрат; АВ = а; ΔВСМ - тупоугольный равнобедренный; ∠В = 120°; ABCD ⊥ ΔВСМ. Найти: SΔADM. Решение: Угол между двумя плоскостями ABC и МВС - ∠MKN; ∠MKN - прямой (по условию) ⇒ ΔMKN - прямоугольный; МК - высота ΔМВС; |
III. Подведение итогов
Разобрать задачи, предложенные в самостоятельной работе.
Домашнее задание
Подготовиться к зачету.
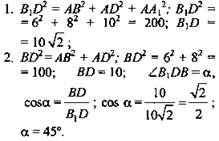
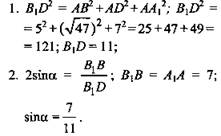
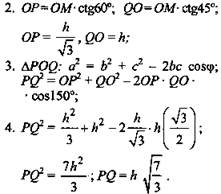 (Ответ:
(Ответ: