Поурочные разработки по геометрии 10 класс
Прямоугольный параллелепипед - ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) ввести понятия прямоугольного параллелепипеда;
2) рассмотреть свойства его граней, двугранных углов, диагоналей.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели.
II. Проверка домашнего задания
Двое учеников у доски записывают решение домашнего задания:
№ 173 и № 174.
№ 173. Дано: ABCD - тетраэдр; CD ⊥ (ABC); АВ = ВС = АС = 6; BD = 3√7 (рис. 1).
Найти: двугранные углы DACB, DABC, BDCA.
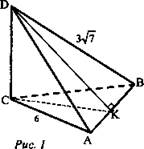
Решение:
1) Так как DC ⊥ (ABC), то DCA ⊥ ABC пo признаку перпендикулярности двух плоскостей, двугранный угол DAСВ - прямой.
2) Проведем СК ⊥ АВ, тогда АВ ⊥ DK (по теореме о трех перпендикулярах), значит, ∠DKC - линейный угол двугранного угла при АВ. Из ΔАСК: СК = АС · sin 60°, ![]() Из BDK: ВК = 1/2, АВ = 3 (СК - высота равнобедренного треугольника). По теореме Пифагор.
Из BDK: ВК = 1/2, АВ = 3 (СК - высота равнобедренного треугольника). По теореме Пифагор.
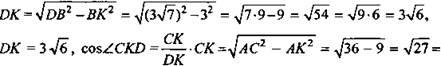
![]() Из прямоугольного ΔDCK по теореме Пифагора
Из прямоугольного ΔDCK по теореме Пифагора ![]() DC находится из прямоугольного ΔDCB - по теореме Пифагор.
DC находится из прямоугольного ΔDCB - по теореме Пифагор.
![]()
![]()
3) Так как ВС ⊥ DC и АС ⊥ DC, то угол ∠ACB линейный угол двугранного угла BDCA. Так как ΔABC - равносторонний ⇒ ∠ACB = 60°, то двугранный угол равен 60°. (Ответ: 60°, 45°, 90°.)
№ 174. Дано: ABCD - тетраэдр; АС = СВ = 5; DB = 5√5 ; ∠DAB = ∠DAC = ∠ACB = 90° (рис. 2).
Найти: двухранные углы тетраэдра ABCD.
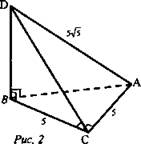
Решение: DA ⊥ АВ, DA ⊥ АС ⇒ DA ⊥ AВС, значит, АС - проекция DC на плоскость ABC, ∠ABC = 90°, ВС ⊥ АС, значит, ВС ⊥ DC по теореме о трех перпендикулярах, ∠ACD - линейный угол двугранного угла ABCD. Из ΔACD: ![]()
![]() Из ΔDCA:
Из ΔDCA: ![]() (Ответ: 60°.)
(Ответ: 60°.)
Двое учеников решают по карточкам: Дано: ABCD - тетраэдр; DC = 8 см, СВ = 6 см; AD ⊥ ABC; ∠DCB = 90°, ∠DBA = 45° (рис. 3).
Найти: AD.

Решение: ΔDCB: ![]()
![]() ΔDAB - прямоугольный; ∠A = 90°, так как ∠DBA = 45° ⇒ ΔDAB - прямоугольный равнобедренный. AD = АВ = х, по теореме Пифагора
ΔDAB - прямоугольный; ∠A = 90°, так как ∠DBA = 45° ⇒ ΔDAB - прямоугольный равнобедренный. AD = АВ = х, по теореме Пифагора ![]() (Ответ: 5√2.)
(Ответ: 5√2.)
Дано: МАВС - тетраэдр, МА ⊥ ABC, МС = 4 см; СВ = 6 см, ∠CAB = 120°; АС = АВ (рис. 4).
Найти: MB, ABC.
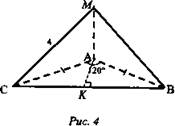
Решение: ΔСМВ: MB = СМ = 4 см (так как СА = АВ, МА ⊥ САВ ⇒ наклонные тоже будут равны; в ΔСАВ проведем высоту АК, так как СА = АВ по условию ⇒ ΔСАВ - равнобедренный. АК - является медианой и высотой; ![]()
![]() КВ2 = АВ2 - АК2; обозначим АК = х, получим уравнение:
КВ2 = АВ2 - АК2; обозначим АК = х, получим уравнение: ![]()
![]()
![]() (Ответ: 30°.)
(Ответ: 30°.)
Остальные учащиеся решают задачу.
Постройте сечение параллелепипеда ABCDA1B1C1D1, которое проведено через середины ребер АВ, AD и А1В1. Каким многоугольником является это сечение?
Дано: ABCDA1B1C1D1 - параллелепипед, L ∈ A1B1, L - середина A1B1, М ∈ AD, М - середина AD; К ∈ АВ, К - середина АВ (рис. 5).
Построить: 1) сечение LKM; 2) Каким многоугольником является сечение.
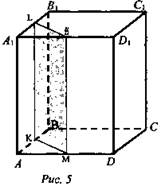
Построение:
1) LKM ∩ А1АВ = L.
2) LKM ∩ ABC = М.
3) Грани ABC параллельны А1В1С1, значит, отрезки сечения параллельны.
4) Строим LN || KM.
5) KLNM - параллелограмм.
Ответьте на вопросы:
- Что называется параллелепипедом?
- Грани, вершины, противоположные вершины, противоположные ребра, диагональ параллелепипеда.
- Свойства параллелепипеда.
Объяснение темы
1) Определение прямоугольного параллелепипеда
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
2) Свойства прямоугольного параллелепипеда:
1. В прямоугольном параллелепипеде все шесть граней - прямоугольники.
Полуплоскости, в которых расположены смежные грани параллелепипеда, образуют двугранные углы, которые называются двугранными углами параллелепипеда.
2. Все двугранные углы прямоугольного параллелепипеда - прямые.
Самостоятельно доказать свойство.
3) Понятия измерений прямоугольного параллелепипеда.
4) Теорема: ![]()
Доказательство предлагается учащимся выполнить самостоятельно.
Дано: ABCDA1B1C1D1 - параллелепипед.
Доказать: ![]()
Доказательство: так как СС1 ⊥ ABCD ⇒ ∠ACC1 - прямой из прямоугольника ΔАСС1: по теореме Пифагора ![]() АС - диагональ прямоугольника ABCD, поэтому
АС - диагональ прямоугольника ABCD, поэтому ![]() следовательно,
следовательно, ![]() теорема доказана.
теорема доказана.
Следствие: диагонали параллелепипеда равны.
Предложить учащимся назвать все диагонали: ![]()
III. Формирование навыков и умений учащихся
№ 187 в. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; АВ = √39 ; AD = 7; АА1 = 9.
Найти: АС1.
Решение: ![]()
![]() (Ответ: 13.)
(Ответ: 13.)
№ 190 в. Дано: ABCDA1B1C1D1 - куб; К - середина A1D1 (рис. 6).
Найти: Двугранный угол А1ВВ1К.
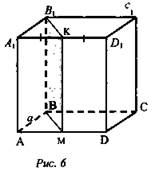
Решение: Плоскости ![]()
![]() значит,
значит, ![]() значит,
значит, ![]() (по определению перпендикулярной прямой и плоскости); ∠А1В1К — линейный угол двугранного угла КВ1ВА из прямоугольного ΔА1В1К; ∠A1 - прямой,
(по определению перпендикулярной прямой и плоскости); ∠А1В1К — линейный угол двугранного угла КВ1ВА из прямоугольного ΔА1В1К; ∠A1 - прямой, ![]()
![]() (К - середина A1D1 - по условию); А1В1 = а — все ребра у куба равны;
(К - середина A1D1 - по условию); А1В1 = а — все ребра у куба равны; ![]()
![]() (Ответ:
(Ответ: ![]() )
)
№ 193. Дано: ABCDA1B1C1D1 - параллелепипед. D1B = d; AC = m; AB = n (рис. 7).
Найти: расстояние между прямой DD1 и плоскостью АСС1.
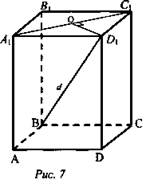
Решение: DD1 || АА1С1 (так как DD1 || АА1, признак параллельности прямой и плоскости). Проведем ![]()
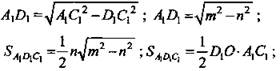
![]() (Ответ:
(Ответ: ![]() )
)
IV. Подведение итогов
Домашнее задание:
П. 24, A - № 1876; 193 а; 190 а; В - 1) № 217.
2) Дано: ABCDA1B1C1D1 - куб; ОМ ⊥ DC; B1D = d.
Найти: O1М.
Решение: обозначим AD = х, тогда ![]() ; по теореме;
; по теореме; 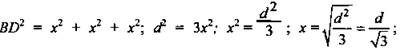
![]() ; по теореме Пифагора
; по теореме Пифагора 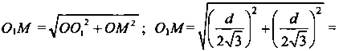
![]() (Ответ:
(Ответ: ![]() )
)
№ 1876. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; АВ = 8; ВС = 9; AA1 = 12 (рис. 9).
Найти: АС1.
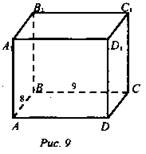
Решение: По теореме ![]()
![]()
![]() (Ответ: 17.)
(Ответ: 17.)
№ 193 а. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; АВ = n, BD = d, BD = m (рис. 10).
Найти: АА1..
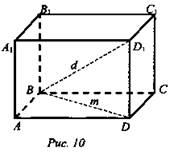
Решение: ![]()
![]() расстояние между плоскостями равно АА1 по свойству прямоугольника BD = АС = m, из прямоугольного ΔBD1D по теореме Пифагора
расстояние между плоскостями равно АА1 по свойству прямоугольника BD = АС = m, из прямоугольного ΔBD1D по теореме Пифагора ![]()
![]() (Ответ:
(Ответ: ![]() )
)