Поурочные разработки по геометрии 10 класс
Угол между прямой и плоскостью - ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) ввести понятие угла между прямой и плоскостью;
2) рассмотреть задачи, в которых используется это понятие.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
1. Индивидуальная работа у доски.
Один ученик доказывает обратную теорему о трех перпендикулярах (№ 153).
Второй ученик выполняет краткое решение домашних задач № 140, 143.
2. Пока учащиеся готовятся у доски, учитель ведет фронтальную работу с классом.
Вопросы:
- Сформулируйте теорему о трех перпендикулярах (опросить 3-х учащихся).
- Что называется расстоянием между параллельными плоскостями?
- Что называется расстоянием между скрещивающимися прямыми?
- Что называется углом между прямыми?
- Что называется углом между скрещивающимися прямыми?
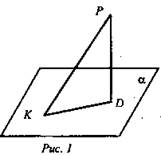
- По рисунку 1 назовите: перпендикуляр, основание перпендикуляра, наклонную к плоскости α, основание наклонной, проекцию наклонной на плоскость α.
- Сравните РК и PD. (РК > PD, так как перпендикуляр PD меньше любой наклонной).
- Что называется расстоянием от точки А до α?
III. Объяснение новой темы
1. Ввести понятия проекции точки на плоскость, проекции фигуры на плоскость.
Вопрос: Что называется проекцией наклонной на плоскость? (Отрезок, соединяющий основание перпендикуляра и основание наклонной.)
Смотрим на рис. 54 учебника или рис. 2 на доске.
- Что изображено на рис. 2? (Плоскость α и ![]() ).
).
Запишем в тетрадях:
Определение
Проекцией точки на плоскость называется основание перпендикуляра, проведенного из этой точки к плоскости, если точка не лежит в плоскости, и сама точка, если она лежит в плоскости.
- Что же является проекцией М на плоскость α? (М1.)
- Что же является проекцией N на плоскость α? (N1 = N.)
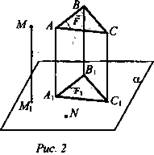
Отметим вне а еще три точки А, В, С, не лежащие на одной прямой. Соединим их попарно.
- Как построить проекцию ΔABC на α? (Провести из А, В, С перпендикуляры на α, получив точки А1, В1, C1, то есть ΔА1В1С1.)
Обозначим ΔABC фигурой F.
- Как же построить проекцию произвольной фигуры F?
Вывод:
Если построить проекции всех точек какой-нибудь фигуры F на данную плоскость α, то получим фигуру F1, которая называется (является) проекцией фигуры F на данную плоскость.
2. Докажем, что проекцией прямой (а) на плоскость (α), не перпендикулярную к этой прямой, является прямая. Рис. 55, стр. 43 учебника.
На доске рис. 3.
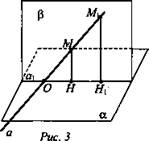
Учащиеся записывают краткую запись в тетрадях (учитель на доске).
Дано: ![]()
Доказать: проекцией а на α является а1.
Доказательство:
1) ![]() Проведем β через а и МН,
Проведем β через а и МН, ![]()
2) Возьмем ![]()
3) Так как ![]() то есть Н1 проекция М1 на α.
то есть Н1 проекция М1 на α.
Вопрос: Что мы доказали?
Ответ: Что проекция произвольной прямой точки прямой а лежит на прямой a1.
Верно и то, что любая точка прямой a1 является проекцией некоторой точки прямой а, ⇒ а1 проекция а на α.
3. Определение угла между прямой и плоскостью (рис. 4).
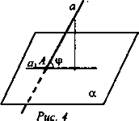
0° < α ≤ 90°.
Предложить учащимся сформулировать определение.
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярную к ней, называется угол между прямой и ее проекцией на плоскость.
Запишем его кратко в тетрадях (рис. 4 и определение).
Если ![]() а1 проекция а на α, то
а1 проекция а на α, то ![]() это величина, а не фигура.
это величина, а не фигура.
Вопрос: А что если а ⊥ α или а || α?
Ответ оформить в тетрадях в виде таблички, замечания.
Замечания:
1. Если а ⊥ α, то проекция а на α является А.
|
Если а || α, то проекция а на α, а1.
Понятие угла не вводим. .
|
IV. Закрепление изученного материала
1. Решение задачи № 165
Дано: ![]() наклонные,
наклонные, ![]() (рис. 5.)
(рис. 5.)
Найти: ВС.
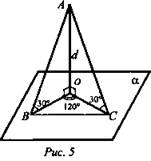
Решение:
1) ΔВАО = ΔСАО (по катету и острому углу, противолежащему катету). ОВ = ОС. ΔВАО, ![]()
2) ΔВОС: по теореме косинусов ![]()
![]() (Или ΔВОС - равнобедренный. Проведем
(Или ΔВОС - равнобедренный. Проведем ![]() ОН - биссектриса, медиана.
ОН - биссектриса, медиана. ![]() ). (Ответ: 3d.)
). (Ответ: 3d.)
2. Самостоятельно решить при наличии времени. Чертеж с условием на доске.
Дано: ![]() (рис. 6).
(рис. 6).
Найти: ∠ADC.
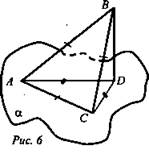
Решение: ΔABD = ΔCBD по гипотенузе и катету. Пусть AD = а, ![]()
![]() ΔАDC - равнобедренный (рис. 7).
ΔАDC - равнобедренный (рис. 7).
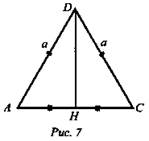
DH ⊥ AC, DH - высота, медиана и биссектриса ![]() ∠ADC = 90°. (Ответ: 90°.)
∠ADC = 90°. (Ответ: 90°.)
3. При наличии времени задача 162 учебника (стр. 46, рис. 57) разобрана. Учащимся записать в тетрадь краткую запись решения и сделать вывод с учителем. (Если нет времени, на дом.)
Дано: М ∈ α, МА - наклонная, А ∈ α, ![]()
Доказать: φ0 < φ.
Доказательство: ![]()
Пояснение: 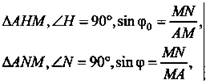 AM - общая гипотенуза.
AM - общая гипотенуза.
Вывод: Угол между прямой и ее проекцией на плоскость есть наименьший из углов данной прямой и прямыми, лежащими в этой плоскости и проходящими через точку пересечения данной прямой с плоскостью.
V. Подведение итогов
Вопросы: Какие новые понятия мы изучили на уроке? (Проекции точки на плоскость, проекции фигуры на плоскость, угол между прямой и плоскостью.)
Дадим определение этим понятиям (опрос 3-х учащихся). Выставление оценок.
Домашнее задание
П. 21.
Если не успели, № 162, рис. 57, стр. 46.
№ 163, 164.
Напомнить: длины отрезков касательных, проведенных из одной точки до точки касания, равны. Гипотенуза вписанного прямоугольного треугольника является диаметром окружности.
Решить задачу: Найдите периметр прямоугольного треугольника, если радиус вписанной окружности равен 1, а радиус описанной окружности равен 2, 5 (рис. 8).
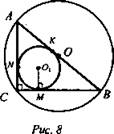
Решение: ΔABC, АО = 2,5, АВ = 5, NC = СМ = ОМ1 = 1. Пусть AN = х, АК = х, КВ = MB = 5 - х. По теореме Пифагора: ![]()
![]() (Ответ: 12.)
(Ответ: 12.)
№ 163. Дано: ![]() AM - наклонная, AM = d, МН - проекция наклонной; a) ∠AMH = 45°, б) ∠AMH = 60°, в) ∠AMH = 30° (рис. 9).
AM - наклонная, AM = d, МН - проекция наклонной; a) ∠AMH = 45°, б) ∠AMH = 60°, в) ∠AMH = 30° (рис. 9).
Найти: МН.
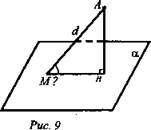
Решение: АН ⊥ α, МН - проекция наклонной AM. ΔАМН, ∠H = 90°, ![]()
![]()

(Ответ: ![]() )
)
№ 164
Дано: A ∉ α, AB - наклонная, ![]()
![]() (рис. 10).
(рис. 10).
Найти: угол между АВ и α.
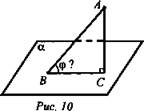
Решение: ![]()
![]()
![]() (Ответ: 60°.)
(Ответ: 60°.)