Поурочные разработки по геометрии 10 класс
Предмет стереометрии. Аксиомы стереометрии - АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ
Цели урока:
1) ознакомить учащихся с содержанием курса стереометрии;
2) изучить аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве.
Ход урока
I. Организационный момент
II. Новый материал
Учитель знакомит с понятием стереометрии: Мы с вами с 7 класса начали знакомиться со школьным курсом геометрии.
Вопрос кучащимся: что такое геометрия? (Геометрия - наука о свойствах геометрических фигур. Слово «геометрия» - греческое, в переводе - «землемерие». Такое название связано с применением геометрии для измерений на местности.) В 7-9 классах мы с вами изучали первый раздел геометрии - планиметрию.
Вопрос к учащимся: что такое планиметрия? (Планиметрия - раздел геометрии, в котором изучаются свойства фигур на плоскости.)
Вспомним основные понятия планиметрии (см. плакат 1) (точка, прямая: обозначение, изображение).
Плакат 1

Необходимо отметить, что эти понятия не определяемы, они принимаются интуитивно.
Сегодня мы приступим к изучению нового раздела геометрии - стереометрии.
Определение учащиеся записывают в тетрадь под руководством учителя (стр. 3 учебника): Стереометрия - раздел геометрии, в котором изучается свойства фигур в пространстве.
Основные фигуры в пространстве: точка, прямая и плоскость (см. плакат 1).
Представление плоскости дает гладкая поверхность стены, стола.
Плоскость как геометрическую фигуру следует представлять себе простирающейся во все стороны, не ограниченной.
Учитель изображает на доске, учащиеся в тетради.
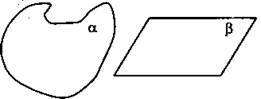
Плоскости обозначаются греческими буквами α, β, γ и т. д.
Необходимо отметить, что об этих фигурах мы имеем наглядное представление, но определения этих фигур в геометрии не даются. Их свойства выражены в аксиомах. С ними мы познакомимся немного позже.
Наряду с точкой, прямой и плоскостью в стереометрии рассматривают геометрические тела, изучают их свойства, вычисляют их площади и объемы. Представление о геометрических телах дают окружающие нас предметы.
Учитель показывает модели и приводит примеры из окружающей действительности (см. плакат 2).
Плакат 2
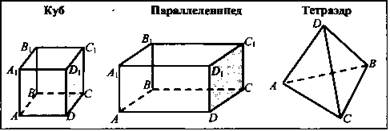
Учащиеся изображают в тетрадях куб и выделяют другим цветом некоторые элементы (точки, отрезки), например: точка А, отрезок ВС.
Теперь рассмотрим аксиомы стереометрии.
Вопрос к учащимся:
1) Что такое аксиома? (Аксиома - утверждение о свойствах геометрических фигур, принимается в качестве исходных положений, на основе которых доказываются далее теоремы и вообще строится вся геометрия.)
2) Какие аксиомы планиметрии вы знаете?
- через любые две точки можно провести прямую, и притом только одну.
- из трех точек прямой одна, и только одна, лежит между двумя другими.
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.
А1. Через любые 3 точки, не лежащие на одной прямой, проходит плоскость и притом только одна.
Учащиеся под руководством учителя выписывают в тетрадь из учебника (стр. 5) аксиому A1. Делают рисунок а) с плаката 3:
Плакат 3
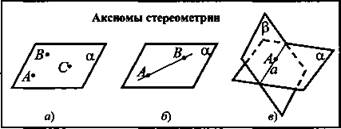
Важно отметить, что если взять не 3, а 4 произвольные точки, то через них может не проходить ни одна плоскость, то есть 4 точки могут не лежать в одной плоскости.
А2. Если 2 точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости (см. плакат 3, рис. б).
Ученики делают запись и рисунок в тетрадь.
В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.
А3. Если 2 плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Говорят, плоскости пересекаются по прямой (см. плакат, 3 рис. в).
Ученики делают запись на рисунок в тетрадь.
III. Закрепление изученного материала
1. Прочитать формулировки аксиом А1-А3.
2. Решаем задачи:
Учащиеся читают условие задачи по учебнику стр. 7-8 и дают ответ с объяснениями.
Задача 1 (а, б) с. 7.
Ответ:
а) Точки Р и Е лежат в плоскости (ADB), а значит и прямая РЕ лежит в плоскости (ADB) (по А2). Аналогично МК лежит в плоскости (BDC). Точки В и D лежат одновременно в плоскостях (ADB) и (ВDC), а значит прямая BD лежит в плоскостях (ADB) и (ABC).
Аналогично АВ лежит в плоскостях (ADB) и (ABC).
Точки С и Е лежат одновременно в плоскостях (ABC) и (DEC), а значит прямая СЕ лежит в этих же плоскостях.
б) Заметим, что точка С лежит на прямой (DK) и в плоскости ABC, а следовательно, DK ∩ (ABC) в точке С, так как точек пересечения более одной (прямая не лежит в плоскости), то это единственная точка.
Аналогично СЕ пересекается с плоскостью (ADB) в точке Е.
Задача 2 (a) с. 7.
Ответ: а) В плоскости DCC1. D, С, С1, D1, К, М, R (см. № 1). В плоскости BQC: В1, В, Р, Q, C1, М, С.
IV. Подведение итогов
Мы познакомились с новым разделом геометрии - стереометрией, узнали новые аксиомы и использовали их при решении задач.
Объявление оценок (с комментариями).
Домашнее задание
Повторить аксиомы планиметрии.
Выучить аксиомы A1-A3.
Прочитать пункт 1-2.
Задача 1 (в, г)
Ответы:
в) в плоскости ADB лежат точки: A, D, В, Е, Р, М, так как точка Е лежит на прямой АВ, а значит, и в плоскости ABD. В плоскости DBC лежат точки: D, В, С, М, К.
г) плоскости АВС и DCB пересекаются прямой ВС, так как обе точки В и С лежат в обеих плоскостях. Аналогично: ABD пересекается с CDА по прямой AD. Так как точка Е принадлежит PD, значит, Е принадлежит PDC и так как точка С принадлежит PDC, то прямая СЕ принадлежит PDC, а так как СЕ принадлежит ABC, то плоскости АВС и PDC пересекаются по прямой СЕ.
Задача 2 (б, д)
Ответы:
б) АА1В1; AA1D1.
д) ![]()
Дополнительно:
Вариант I
3. [а) да, см. А1 б) нет в) нет. В качестве примера можно взять квадрат г) да - это A1].
Вариант II
4. (а) [нет. Если А, В, С лежат на одной прямой, то через А, С, D можно провести плоскость (А1). Тогда точка В лежит в плоскости α, так как точка В лежит на прямой АС, а значит, точки А, В, С, D лежат в одной плоскости].
Вариант III
4. (б) [нет. Так как, если АВ и CD пересекаются, то через них можно провести плоскость (это теорема), а значит, А, В, С, D лежат в одной плоскости. Противоречие.]