Решение задач по теме «Параллельность прямой и плоскости» - урок 3 - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ - ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Цели урока:

1) обобщить материал изученного параграфа;

2) развивать навык применять изученные теоремы к решению задач;

3) воспитывать самостоятельность в выборе способа решения задач;

4) контроль знаний учащихся.

Ход урока

I. Организационный момент

Сообщить тему и цели урока

II. Проверка домашнего задания

Проверка задач № 23, 25 устно, № 88 подготовить на доске.

III. Актуализация знаний учащихся

Устная работа.

1) Верно ли утверждение параллельности прямой и плоскости: «Прямая, параллельная какой-либо прямой на плоскости, параллельна и самой плоскости». (Нет, прямая может лежать в плоскости.)

2) Прямые а и b параллельны. Какое положение может занимать прямая а относительно плоскости, проходящей через прямую b?(а параллельна плоскости.)

3) Даны прямая и две пересекающиеся плоскости. Охарактеризовать все возможные случаи их взаимного расположения. (Прямая параллельна двум плоскостям, параллельна одной и пересекает другую, пересекает две плоскости.)

4) Одна из двух параллельных прямых параллельна некоторой плоскости. Можно ли утверждать, что и вторая прямая параллельна этой плоскости? (Да.)

5) Даны две пересекающиеся плоскости. Существует ли плоскость, пересекающая две данные плоскости по параллельным прямым? (Да.)

6) В плоскости α даны две пересекающиеся прямые а и b. Точка С не лежит в плоскости α. Каковы возможные случаи расположения прямой, проходящей через точку С, относительно прямых а и b? (Проходят через точку пересечения а и b.)

IV. Решение задач

№ 27. Дано: (рис. 1).

Доказать:

Найти: BE.

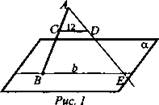
Решение:

1. Проведем плоскость (ACD). CD || b; если но получили противоречие, значит

2. ΔADC ~ ΔАЕВ (по трем углам); (Ответ: 48 см.)

V. Проверочная самостоятельная работа (см. приложение)

Ответы и указания к задачам самостоятельной работы

I уровень

Вариант I

1. Дано: (рис. 2).

Доказать: ΔDBD1 ~ ΔABC.

Найти: AC.

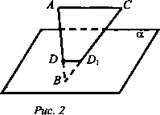
Решение:

1) - по признаку, значит, ∠B - общий для ΔАВС и ΔDBD1. Следовательно, ΔDBD1 ~ ΔАВС.

2) Из ΔABC ~ ΔDBD1 ⇒ (Ответ: 12 см.)

2. Дано: (рис. 3).

Доказать:

Доказательство:

1) по теореме о трех параллельных прямых

2) Аналогично b || α.

Вариант II

1. Дано: (рис. 4).

Доказать: ΔDBD1 ~ ΔABC.

Найти: DD1.

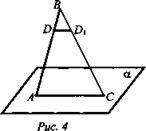
Решение:

1) DD1 || α (по условию), (ABC) ∩ α = АС, АС ∈ α, DD1 || α, DD1 || АС - по признаку.

2) ΔАВС ~ ΔDBD1 (по трем углам), ∠В - общий, ∠BDD1 = ∠BAC, (Ответ: 3 см.)

2. Дано: (рис. 5).

Доказать: с || γ.

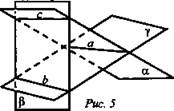
Доказательство:

1) Пусть

2)

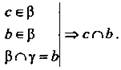
3) Из 1) и 2) следует с ∈ γ, чего быть не может.

II уровень

Вариант I

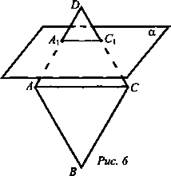
1. Дано: ABCD - параллелограмм; (рис. 6).

Доказать: ΔC1DA1 ~ ΔАВС.

Найти: АС.

Решение.

1) по утверждению

2) Рассмотрим ΔADC, ΔA1DC1: ∠D - общий, ∠DA1C1 = ∠DAC, ∠DC1A1 = ∠DCA - как соответствующие при параллельных прямых, значит ΔADC ~ ΔА1DC1 (по трем углам).

3) Рассмотрим ΔАВС и ΔACD. АВ = CD, ВС = AD - по свойству параллелограмма, АС - общая, то есть ΔАВС = ΔACD.

4) Из п. 2 ΔADC ~ ΔA1DC1; (Ответ: 15 см.)

2. Дано: (рис. 7).

Доказать: a || b.

Доказательство:

1) Пусть a ∩ b, тогда М = а ∩ α, а ∩ β = М, но а || α и а || β, значит, получили противоречие, то ест.

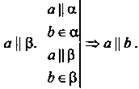
Вариант II

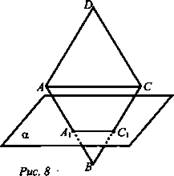
1. Дано: ABCD - параллелограмм; (рис. 8).

Доказать: ΔADC ~ ΔА1ВС1.

Найти: AD.

Решение:

1)

2) ΔАВС и ΔА1ВС1: ∠B - общий, ∠ACB = ∠A1C1B, ∠CAB = ∠C1A1B соответствующие при АС || А1С1, значит, ΔАВС ~ ΔА1ВС1.

3) (по свойству параллелограмма), АС — общая.

4) Из п. 2 следует, что ΔАВС ~ Δ А1ВС1. (Ответ: 9 см.)

2. Дано: ABCD - параллелограмм; (рис. 9).

Доказать: b || (ABCD).

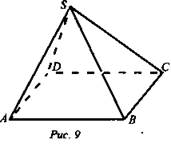
Доказательство: Пусть b ∩ (ABCD), значит в плоскости (SBC), b ∩ ВС, в плоскости (SAD); b ∩ AD, следовательно, но это противоречит условию, значит, b || (ABCD).

III уровень

Вариант I

1. Дано: ABCD - параллелограмм; (рис. 10).

Найти: АВ.

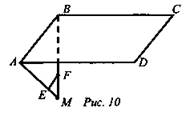
Решение:

1) по теореме о параллельности прямой и плоскости.

2) ΔABM ~ ΔFEM (по трем углам) (Ответ: )

2. Дано: (рис. 11.

Доказать: а || b.

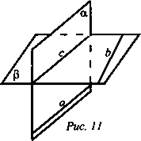
Доказательство:

по теореме о трех параллельных прямых.

Вариант II

1. Дано: ABCD - ромб; (рис. 12).

Найти: FK.

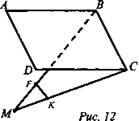
Решение:

1) по теореме о параллельности прямой и плоскости.

2) ABCD - ромб, значит, BC = AD. ΔMFK ~ ΔМВС (по трем углам.

(Ответ: )

2. Дано: (рис. 13).

Доказать: а || b.

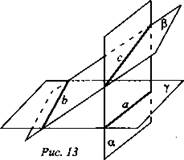
Доказательство:

по теореме о трех параллельных прямых.

VI. Подведение итогов

Домашнее задание

I уровень: № 32 (разобрана в учебнике), № 92.

II уровень: № 33, № 92.

Задача 33

Дано: (рис. 14).

Доказать:

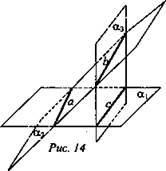
Доказательство:

1) Никакие две прямые не пересекаются, тогда они параллельны, так как а и b ∈ α2, значит, а || b. Аналогично b || с, а || с.

2) Любые две прямые, например а ∩ b = М, значит, М ∈ α1, М ∈ α2, M ∈ α3, а тогда, значит, М лежит во всех плоскостях и b ∩ с = М.

3) а = b, тогда прямые являются пересечением всех трех плоскостей α1, α2, α3, а значит, плоскости проходят через одну прямую, что противоречит условию.