Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Область определения. Периодичность
23.1. С одной стороны, log3sin x ≤ 0, так как sin x ≤ 1, а с другой стороны, log3sin x ≥ 0, так как это выражение стоит под знаком квадратного корня. Остается единственная возможность:
log3sin x = 0, sin x = 1, x = π(4n + 1)/2.
Ответ. π(4n + 1)/2.
23.2. Чтобы найти область определения данной функции, нужно решить систему
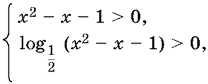
которая эквивалентна неравенству
0 < x² − x − 1 < 1, или (х² − x − 1)(х² − x − 2) < 0,
т. е.
(x − 1 − √5/2)(x − 1 + √5/2)(x + 1)(x − 2) < 0.
Ответ. −1 < x < 1 − √5/2; 1 + √5/2 < x < 2.
23.3. Данное выражение принимает действительные значения, если x удовлетворяет неравенству
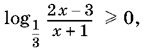
которое равносильно неравенству
![]()
Его можно заменить системой
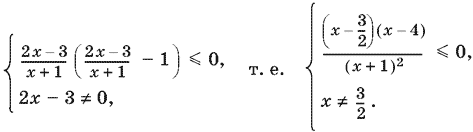
Ответ. 3/2 < x ≤ 4.
23.4. Чтобы существовал арккосинус, необходимо и достаточно, чтобы
−1 ≤ x² − Зх + 1 ≤ 1,
т. е.
(х² − Зх + 2)(х² − Зх) ≤ 0, или x(x − 1)(x − 2)(x − 3) ≤ 0,
откуда
0 ≤ x ≤ 1, 2 ≤ x ≤ 3.
Из найденных интервалов нужно исключить точки, в которых tg 2x не существует, т. е. числа x = π(2n + 1)/4. Два из этих чисел: x = π/4 и x = 3π/4 лежат в найденных интервалах.
Ответ. 0 ≤ x < π/4, π/4 < x ≤ 1, 2 < x < 3π/4, 3π/4 < x ≤ 3.
23.5. Данное выражение принимает действительные значения, если удовлетворяется система неравенств
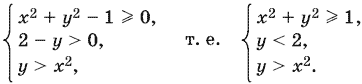
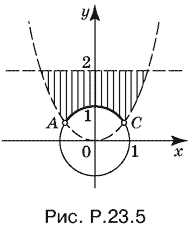
Решением этой системы будет часть плоскости, лежащая внутри параболы y = x², вне круга x² + y² = 1 и ниже прямой y = 2, причем точки, лежащие на границе и принадлежащие или прямой, или параболе, не входят в область, а точки, лежащие на окружности (кроме точек А и С — рис. P.23.5), входят в область определения.
23.6. Способ 1. Пусть Т — период функции. Тогда
cos (x + Т)² = cos x²
при всех x. Если x = 0, то получим cos Т² = 1, откуда Т² = 2nπ. Если x = Т√2 , то cos (√2 + 1)²Т² = cos 2Т², откуда или
(√2 + 1)²Т² + 2Т² = 2kπ, или (√2 + 1)²Т² − 2Т² = 2mπ,
т. е.
либо (2 + 2√2)Т² = 2kπ, либо (1 + 2√2)Т² = 2mπ.
Подставляя в оба выражения Т² = 2nπ, получим соответственно
5 + 2√2 = k/n или 1 + 2√2 = m/n,
что невозможно, так как слева стоят иррациональные числа, а справа — рациональные.
Способ 2. Найдем корни функции cos x²:
![]()
Рассмотрим положительные корни
![]()
Предположим, что Т > 0 — период функции. Тогда, если при x = х1 функция равна нулю, то и при x = x1 + Т она тоже равна нулю. Другими словами, х1 + Т = xm. Аналогично x2 + Т = хk. Вычитая одно равенство из другого, получим
![]()
т. е.
![]()
Возведем в квадрат:
![]()
После вторичного возведения в квадрат получим
![]()
Это равенство возможно лишь при
![]()
, так как все остальные его элементы — целые. Однако числа k и m выбраны так, что k ≥ 3 и m ≥ 2, т. е. k + m > 3.
23.7. Если f(x) — периодическая функция с периодом Т, то при всех x должно выполняться тождество
sin (x + Т) + cos [а(x + Т)] = sin x + cos аx.
Положив в этом тождестве x = 0, x = −Т и x = Т, получим
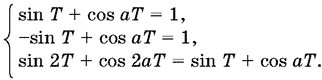
Из первого и второго равенств найдем cos aT = 1 и T = 2nπ/a. Подставим найденное значение Т в последнее уравнение:
sin 4nπ/a + cos 4nπ = sin 2nπ/a + cos 2nπ,
т. е.
sin 4nπ/a = sin 2nπ/a,
откуда или 4nπ/a − 2nπ/a = 2kπ, или 4nπ/a + 2nπ/a = (2k + 1)π, т. e. или а = n/k, или a = 6n/2k + 1. И в том и в другом случае а — рациональное число.
23.8. Период функции cos 3x/2 равен Т1 = 2π : 3/2 = 4π/3, период функции sin x/3 равен 6π.
Наименьшее общее кратное этих периодов будет 12π. Очевидно, что 12π — период данной функции. Докажем, что это — основной период.
Пусть существует период τ такой, что 0 < τ < 12π. Тогда имеем тождество
cos 3/2(x + τ) − sin x + τ/3 − cos 3/2x + sin x/3 = 0,
или
sin ¾ τ sin ¾ (2x + τ) + sin τ/6 cos 1/6 (2x + τ) = 0.
Так как τ < 12π, а ¾τ = 3τ/4ππ и τ/6 = τ/6ππ, то одно из чисел 3τ/4π или τ/6π не является целым, т. е. по крайней мере одно из чисел sin ¾τ и sin τ/6 не равно нулю. Пусть, например, sin ¾τ ≠ 0.
Тогда имеем тождество
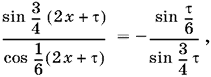
что невозможно, так как в правой части стоит постоянная величина. Легко убедиться, что это тождество ложно, выбрав, например, x = 0 и x = 6π и сравнив для этих x левые части. Получим sin 3τ/4 = 0, что противоречит предположению.
Ответ. 12π.