Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Суммирование
20.1. Докажем, что
S = ½ + ... + 1/n² < 1.
Так как
1/(1 + k)² < 1/k(1 + k),
то
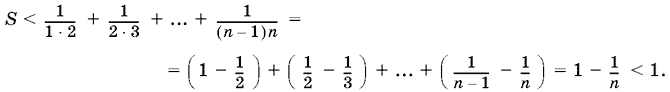
При доказательстве мы воспользовались тем, что
1/(n − 1)n = 1/n − 1 − 1/n.
Такой прием часто применяется и называется разложением дроби на простейшие.
20.2. Так как
![]()
то
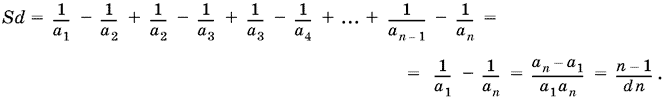
Ответ. n − 1/d²n.
20.3. Представим k−e слагаемое в виде
![]()
Тогда
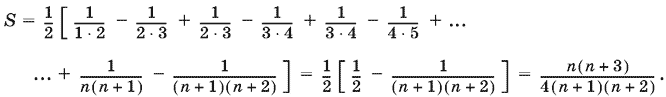
Ответ.
![]()
20.4. Левую часть данного равенства перепишем в виде
![]()
воспользовавшись для этого формулой суммы членов геометрической прогрессии. Тогда (поскольку а ≠ 1)
![]()
Правая часть может быть записана так:
![]()
Итак,
![]()
По условию а ≠ 0, 1, −1. Это позволяет найти нужную нам зависимость.
Ответ. n + 1 = 2k + 1.
20.5. Расположим коэффициенты данного многочлена слева направо и разместим под ними коэффициенты того же многочлена, расположенные в обратном порядке,
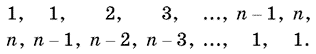
Теперь можно выписать коэффициент при xn, составив сумму попарных произведений расположенных один под другим множителей:
1 · n + 1(n − 1) + 2(n − 2) + 3(n − 3) + ... + (n − 1)1 + n · 1.
Эту сумму можно преобразовать так:
![]()
Каждую из сумм, стоящих в скобках, легко подсчитать:
![]()
Таким образом, искомый коэффициент равен
![]()
Ответ.
![]()
20.6. Неравенство равносильно системе (в левой его части — абсолютная величина суммы членов бесконечно убывающей геометрической прогрессии со знаменателем — 2x):
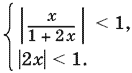
Из второго неравенства следует, что −1 < 2x < 1, т. е. 1 + 2x > 0. Поэтому первое неравенство можно переписать в виде
|x|/1 + 2x < 1, или |x| < 1 + 2x.
Таким образом, приходим к системе
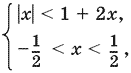
которая равносильна совокупности двух систем
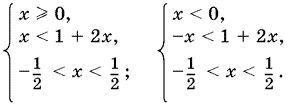
Ответ. −⅓ < x < ½.
20.7. Так как k · k! = (k + 1)! − k!, то
2! − 1! + 3! − 2! + 4! − 3! + ... + (n + 1)! − n! = (n + 1)! − 1.
Ответ. (n + 1)! − 1.
20.8. Домножим Sn на x²:
x²Sn = x³ + 4x5 + 7x7 + ... + (3n − 2)x2n + 1,
и вычтем полученное выражение из Sn:
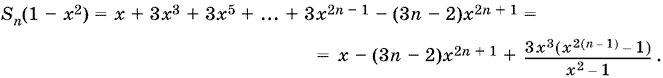
Ответ.
![]()
20.9. Рассмотрим тождество[22]
(x + 1)5 = x5 + 5x4 + 10x³ + 10x² + 5x + 1.
Положим в нем последовательно x = 1, 2, ..., n и сложим n полученных равенств:
25 + 35 + ... + (n + 1)5 = 1 + 25 + 35 + .. + n5 + 5(14 + 24 + ... + n4) + 10(1³ + 2³ + ... + n³) + 10(1² + 2² + ... + n²) + 5(1 + 2 + ... + n) + n.
После приведения подобных получим
![]()
откуда
![]()
Так как
![]()
то
![]()
Многочлен третьей степени, стоящий в скобках, имеет корень n = −2 и поэтому делится на 2n + 1.
Ответ. 1/30 n(n + 1)(2n + 1)(3n² + 3n − 1).
20.10. В n−й группе содержится n членов.
Пусть n четное. Подсчитаем число четных чисел, встречающихся во всех группах до n−й. Это число равно
2 + 4 + 6 + ... + (n − 2) = n(n − 2)/4.
Следовательно, последнее четное число, встречающееся до n−й группы, равно 2n(n − 2)/4 = n(n − 2)/2, а первое четное число, входящее в n−ю группу, равно n(n − 2)/2 + 2. Теперь можно найти сумму n последовательных четных чисел, начинающихся с n(n − 2)/2 + 2. Эта сумма равна
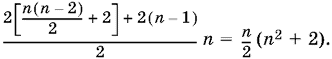
Пусть теперь n четное. Число нечетных членов, встречающихся до n−й группы, равно
1 + 3 + 5 + ... + (n − 2) = (n − 1)²/4.
Последним нечетным числом, стоящим до n−й группы, будет (n − 1)²/2 − 1, а первым числом, входящим в n−ю группу, — число (n − 1)²/2 + 1. Следовательно, сумма n последовательных нечетных чисел, начиная с (n − 1)²/2 + 1, равна
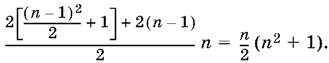
Ответы можно объединить.
Ответ. n/2[n² + 3/2 + (−1)n½].
20.11. Домножим Sn на 2 sin π/2n:
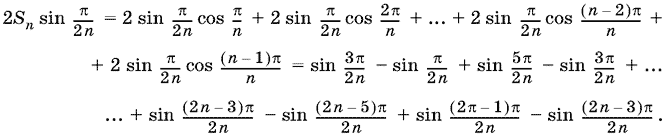
После приведения подобных получим
![]()
Так как sin π/2n ≠ 0 при натуральных n, то Sn = 0.
2 n
Ответ. 0.
20.12. Обозначим искомую сумму через S. Тогда
2S = 1 · 2 + 2 · 2² + 3 · 2³ + ... + 100 · 2100,
2S − S = 100 · 2100 − (1 + 2 + 2² + ... + 299) = 100 · 2100 − (2100 − 1) = 99 · 2100 + 1.
20.13. Пусть искомая сумма равна S. Разделим каждый член данного ряда на 2:
¼ + 3/8 + 5/16 + 7/32 + ... = S/2
и вычтем полученный ряд из данного. Получим ряд:
½ + ½ + ¼ + 1/8 + 1/16 + ...,
сумма которого равна 3/2. Однако, с другой стороны, его сумма есть ни что иное, как S − S/2 = S/2. Таким образом, S/2 = 3/2 и, следовательно, S = 3.
Ответ. 3.