Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Трансцендентные неравенства
15.1. Данное неравенство равносильно такому:
(logsin x 2)² < 2 logsin x 2 + 3.
Обозначив logsin x 2 = y, получим
y² − 2y − 3 < 0,
откуда
−1 < y < 3, или −1 < logsin x 2 < 3.
Последнее неравенство эквивалентно системе
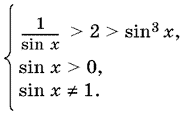
Первое из неравенств системы можно переписать так: 0 < sin x < ½·
Ответ. 2nπ < x < π/6 + 2nπ; 5π/6 + 2nπ < x < π + 2nπ.
15.2. Пусть tg x = √y. Тогда sin² x = y/1 + y, и данное неравенство можно переписать в виде
![]()
(докажите, что последнее преобразование не нарушает равносильности). При 0 < y < 1 и y > 1 получаем различные системы:
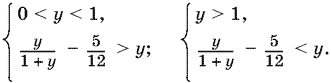
Их можно объединить в одну:
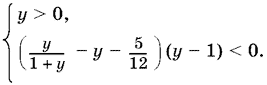
Второе неравенство можно решить методом интервалов
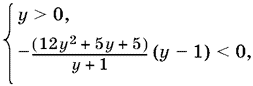
т. е. y > 1.
Итак, tg² x > 1, причем tg x > 0.
Ответ. π/4 + kπ < x < π/2 + kπ.
15.3. Так как выражения, стоящие под знаками логарифмов, должны быть положительными, то указанный в условии интервал можно сузить: 0 < x < π/2. Данное неравенство равносильно системе

Второе неравенство перепишем в виде
sin² x + sin x − 1 < 0,
откуда
![]()
Учитывая, что в интервале 0 < x < π/2 должно быть sin x > 0, получим
![]()
Ответ.
![]()
15.4. Данное неравенство можно переписать так:
log2 cos 2x + log2 sin x + log2 cos x + log2 8 < 0,
т. е.
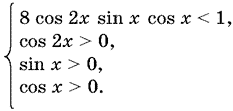
Первое неравенство можно переписать в виде
sin 4x < ½.
Два последних неравенства требуют, чтобы подвижный радиус угла x лежал в первой четверти, а неравенство cos 2x > 0 сужает эту область до первой половины первой четверти (на рис. P.15.4, а — заштрихованный сектор).
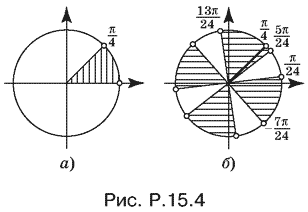
Остается выбрать решения неравенства sin 4x < ½, лежащие в этих промежутках. Все решения неравенства sin 4x < ½ можно записать в виде
−7π/6 + 2nπ < 4x < π/6 + 2nπ,
т. е.
−7π/24 + nπ/2 < x < π/24 + nπ/2
(рис. P.15.4, а). В интересующий нас интервал 0 < x < π/4 из этой серии частично попадут лишь два интервала: −7π/24 < x < 13π/24 (рис. P.15.4, б). Теперь нетрудно написать окончательный ответ.
Ответ. 2nπ < x < π/24 + 2nπ; 5π/24 + 2nπ < x < π/4 + 2nπ.
15.5. Вместо данного неравенства можно написать 0 < |cos x + √3 sin x| < 1, что равносильно системе
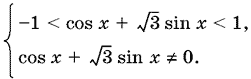
Так как cos x + √3 sin x = 2 cos (x − π/3), то получим
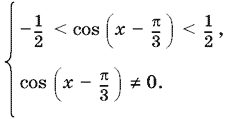
В условии сказано, что 0 ≤ x ≤ 2π, поэтому x − π/3 нужно искать в интервале −π/3 ≤ x − π/3 ≤ 2π − π/3.
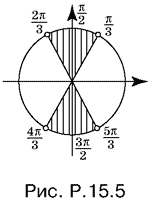
На рис. P.15.5 изображено расположение на тригонометрическом круге значений y = x − π/3, удовлетворяющих последней системе, т. е.
π/3 < x − π/3 < π/2, π/2 < x − π/3 < 2π/3,
4π/3 < x − π/3 < 3π/2, 3π/2 < x − π/3 < 5π/3,
Ответ. 2π/3 < x < 5π/6, 5π/6 < x < π,
5π/3 < x < 11π/6, 11π/6 < x < 2π.
15.6. Неравенство можно переписать так:
cos (|lg x| − π/4) > ½,
откуда
−π/3 + 2nπ < |lg x| − π/4 < π/3 + 2nπ,
т. е.
−π/12 + 2nπ < |lg x| < 7π/12 + 2nπ.
При n < 0 не удовлетворяется правое неравенство.
При n = 0 имеем |lg x| < 7π/12, т. е. −7π/12 < lg x < 7π/12, а потому
![]()
При n = 1, 2, 3, ... имеем −π/12 + 2nπ < lg x < 7π/12 + 2nπ и −7π/12 − 2nπ < lg x < π/12 − 2nπ.
Ответ.
![]()
![]()
n = 1, 2, 3, ... .
15.7. Так как arccos (х² + Зх + 2) ≥ 0, то данное неравенство равносильно системе
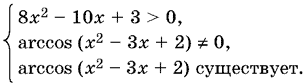
Другими словами,
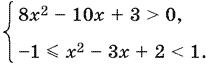
Решаем каждое из трех неравенств системы:

Дискриминант второго неравенства отрицателен, а потому оно удовлетворяется при всех x. Остаются первое и третье:
![]()
Ответ.
![]()
15.8. Если 1 − x ≤ 0, то неравенство не удовлетворяется, так как
arccos (1 − x) ≥ π/2, если 1 − x ≤ 0,
в то время как arctg √x всегда меньше π/2. При 1 − x > 0 обе части неравенства оказываются в интервале от 0 до π/2, где все тригонометрические функции монотонны. Так как косинус в интервале от 0 до π/2 убывает, то данное неравенство равносильно такому:
cos (acrtg √x) < cos (arccos (1 − x))
(большему углу соответствует меньший косинус). Чтобы arccos (1 − x) существовал, необходимо 1 − x ≤ 1. Вспоминая, что 1 − x > 0, получим 0 ≤ x < 1.
Вычислим cos (arctg √x):
![]()
Получаем систему неравенств
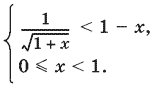
Так как 0 ≤ x < 1, то система равносильна такой:
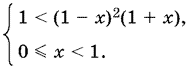
Раскрыв скобки, запишем первое неравенство так: x³ − x² − x > 0, или x(х² − x − 1) > 0. При x = 0 это неравенство не удовлетворяется, а при x > 0 — равносильно неравенству x² − x − 1 > 0. Трехчлен, стоящий в левой части, можно записать так: x(x − 1) − 1. Поскольку x > 0, а x − 1 < 0, то этот трехчлен отрицателен.
Ответ. Нет решений.
15.9. Так как cos² πx + 1 ≥ 1, то второй сомножитель неотрицателен при всех значениях x. Следовательно, неравенство удовлетворяется лишь при положительных значениях сомножителей. Один из них должен быть при этом не меньше единицы. Однако второй не превышает единицы. Для первого же условие 4 x − x² − 3 ≥ 1 равносильно требованию −(x − 2)² ≤ 0, что возможно лишь при x = 2.
Одновременно должно удовлетворяться неравенство
log2(cos² πx + 1) ≥ 1,
которому удовлетворяют числа x = n (n = 0, ±1, ±2, ...). Из них выбираем то, которое обеспечивает равенство единице первого сомножителя.
Ответ. x = 2.
15.10. Обозначим первый сомножитель через А, а второй через В, тогда данное неравенство равносильно совокупности двух систем
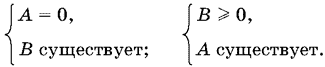
При А = 0 получаем x = 1. Так как при x = 1 В не существует, то первая система не имеет решений.
Перейдем теперь ко второй системе. Для решения неравенства
logtg x (2 + 4 cos² x) ≥ 2
нет необходимости рассматривать случай 0 < tg x < 1, так как А не существует при этих значениях tg x. Если же x > 1, то получим
2 + 4 cos² x ≥ tg² x. (1)
Выражаем tg² x через cos² x (равносильность при такой замене не нарушается):
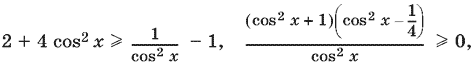
т. е. cos² x ≥ ¼, или
cos x ≤ −½, cos x ≥ ½.
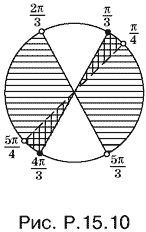
Нанесем решения этих неравенств на тригонометрический круг (рис. P.15.10). Приняв во внимание условие tg x > 1, получим решение системы.
Ответ. π/4 + πk < x ≤ π/3 + πk.