Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Размещения - Элементы комбинаторики - Элементы комбинаторики и теории вероятностей
Цель: рассмотреть следующий вид соединений - размещение.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Определение соединения из n элементов по k.
2. Вычислите:
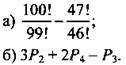
3. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 3, 4, 8?
Вариант 2
1. Определение перестановки из n элементов.
2. Вычислите:

3. Сколько различных трехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 4, 5?
III. Изучение нового материала
Соединения, отличающиеся друг от друга составом элементов или их порядком, каждое из которых содержит k элементов, взятых из n различных элементов, называют размещениями из n элементов по k (k < n).
Другими словами, из n элементов выбирают k элементов и размещают их на k позиций. Число размещений из n элементов по k обозначают символом Ank (читается: А из n по k).
Пример 1
Рассмотрим три элемента а, b, с и выделим две позиции (два места). Будем размещать эти элементы на два места, учитывая порядок следования элементов.
Получаем размещения: ab, ba, ac, ca, be, cb. Число этих размещений A32 = 6.
Получим формулу для вычисления числа размещений n элементов пo k (k < n), т. е. Ank.
Опять учтем комбинаторное правило умножения. На первое место можно поставить любой из n элементов, на второе место - любой из оставшихся (n - 1) элементов и т. д. Тогда на k-е место можно поставить любой из n - (k - 1) = n - k + 1 оставшихся элементов.
Получаем: ![]() Удобнее записать эту формулу в другом виде. Для этого умножим и разделим правую часть равенства на (n - k)! Получаем:
Удобнее записать эту формулу в другом виде. Для этого умножим и разделим правую часть равенства на (n - k)! Получаем: ![]()
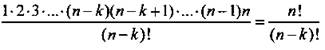 .
.
Итак, имеем ![]()
Очевидно, что при k = n размещения можно рассматривать как перестановки и Аnn = Рn = n! (учтено, что 0! = 1).
Пример 2
Сколько существует трехзначных чисел, в которых цифры различные и нечетные?
Нечетных цифр пять: 1, 3, 5, 7, 9. Их надо разместить на три позиции. Поэтому количество искомых чисел равно числу размещений: ![]()
Пример 3
Сколько трехзначных чисел с различными цифрами можно составить из цифр 0, 1, 2, 3, 4, 5?
Из шести данных цифр можно составить A63 чисел, но среди них будут и трехзначные числа, начинающиеся с нуля (чего, естественно, быть не может). Посчитаем количество таких чисел. В них на первом месте стоит нуль. Значит, на оставшиеся две позиции размещают оставшиеся пять цифр. Поэтому таких чисел будет А52. Следовательно, искомых чисел можно получить: ![]()
![]()
Пример 4
Сколько чисел с разными цифрами можно составить из цифр 0, 1, 2, 3, 4?
Учтем предыдущий пример. Из пяти цифр можно составить А55 пятизначных чисел, в том числе и тех, которые начинаются с нуля (их число А44). Поэтому истинно пятизначных чисел будет: ![]()
Из пяти цифр можно составить А54 четырехзначных чисел, из них начинаются с нуля A43 чисел. Поэтому истинно четырехзначных чисел будет: ![]()
Аналогично находим количество истинно трехзначных чисел: ![]() истинно двузначных чисел:
истинно двузначных чисел: ![]() и однозначных чисел: 5.
и однозначных чисел: 5.
Всего можно составить: 96 + 96 + 48 + 16 + 5 = 261 пятизначных, четырехзначных, трехзначных, двузначных и однозначных чисел.
Пример 5
Вычислим 
Используя формулу для числа размещений, получим: ![]()
![]()
![]()
Пример 6
Найдем натуральное значение n, для которого выполнено условие ![]()
Используем формулы для числа размещений и числа перестановок и запишем условие: ![]() или
или ![]()
![]() или
или ![]() или
или ![]() или 2 = (n - 2)!
или 2 = (n - 2)!
Очевидно, что n - 2 = 2 и n = 4.
IV. Контрольные вопросы
1. Дайте определение размещений.
2. Приведите формулу для вычисления числа размещений.
V. Задание на уроке
№ 754; 757; 759; 761; 762 (а); 763; 764 (б).
VI. Задание на дом
№ 755; 758; 760; 762 (б); 764 (а).
VII. Подведение итогов урока