Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Контрольная работа по теме «Уравнения и неравенства с двумя переменными» - Неравенства с двумя переменными и их системы - Уравнения и неравенства с двумя переменными
Цель: проверка знаний учащихся с использованием разноуровневых вариантов.
Ход урока
I. Сообщение темы и цели урока
II. Варианты контрольной работ.
Вариант 1
1. Решите систему уравнений  способом сложения.
способом сложения.
2. Решите систему уравнений 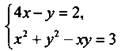 способом подстановки.
способом подстановки.
3. Периметр прямоугольника равен 28 см, а его площадь равна 40 см2. Найдите стороны прямоугольника.
4. Изобразите на координатной плоскости множество решений:
а) уравнения 2|х| + |у| = 4;
б) системы неравенств 
5. Изобразите на координатной плоскости множество решений неравенства (у - 2х)(у + х + 1) < 0.
Вариант 2
1. Решите систему уравнений  способом сложения.
способом сложения.
2. Решите систему уравнений  способом подстановки.
способом подстановки.
3. Периметр прямоугольника равен 26 см, а его площадь равна 42 см2. Найдите стороны прямоугольника.
4. Изобразите на координатной плоскости множество решений:
а) уравнения |х| + 2|у| = 4;
б) системы неравенств 
5. Изобразите на координатной плоскости множество решений неравенства (у + 2х)(у – х - 1) < 0.
Вариант 3
1. Решите систему уравнений.
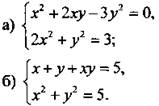
2. Произведение двух натуральных чисел равно 154, а сумма их квадратов равна 317. Найдите эти числа.
3. Изобразите на координатной плоскости множество решений.
а) уравнения х2 - 6х + у2 + 4у = 3;
б) системы неравенств 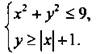
4. Изобразите на координатной плоскости множество решений уравнения 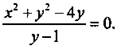
Вариант 4
1. Решите систему уравнений.
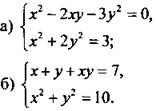
2. Произведение двух натуральных чисел равно 187, а сумма их квадратов равна 410. Найдите эти числа.
3. Изобразите на координатной плоскости множество решений:
а) уравнения х2 + 4х + у2 - 2у = 1;
б) системы неравенств 
4. Изобразите на координатной плоскости множество решений уравнения ![]()
Вариант 5
1. Решите систему уравнений.
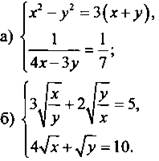
2. Найдите все пары (х; y) целых чисел х и у, являющиеся решениями системы уравнений 
3. Если велосипедист увеличит скорость на 5 км/ч, то получит выигрыш во времени 12 мин при прохождении некоторого пути. Если же он уменьшит скорость на 8 км/ч, то потеряет 40 мин на том же пути. Найти скорость велосипедиста и длину пути.
4. Изобразите на координатной плоскости множество решений:
а) уравнения |у2 - х2| = у + х;
б) неравенства |3х - у + 1| ≤ 2.
Вариант 6
1. Решите систему уравнений.

2. Найдите все пары (х; у) целых чисел х и у, являющиеся решениями системы уравнений 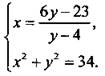
3. Если велосипедист увеличит скорость на 9 км/ч, то получит выигрыш во времени 27 мин при прохождении некоторого пути. Если же он уменьшит скорость на 5 км/ч, то потеряет 29 мин на том же пути. Найти скорость велосипедиста и длину пути.
4. Изобразите на координатной плоскости множество решений:
а) уравнения |у2 – х2| = у - х;
б) неравенства |2х + у - 2| ≤ 1.