Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Свойства и графики основных функций - Функции и их свойства - Квадратичная функция
Цель: вспомнить изученные ранее функции и их свойства.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Найдите значения функции у(-2) · y(1).

2. Найдите область определения функции.
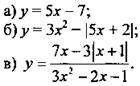
Вариант 2
1. Найдите значения функции у(-3) · у(2).
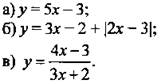
2. Найдите область определения функции.

III. Изучение нового материала
1. Свойства функции
Как уже известно из курса 7-8 классов, любая функция характеризуется определенными свойствами. Часть этих свойств была рассмотрена ранее. Теперь необходимо систематизировать эти свойства и рассматривать их при исследовании любых функций и построении их графиков.
Остановимся теперь на свойствах функции. С двумя свойствами функции вы уже знакомы - это область определения и область значений функции. Рассмотрим следующее свойство функции - точка пересечения графика функции с осями координат.
Так как ось Оу характерна тем, что любая точка на ней имеет координату х = 0, а для оси Ох - любая точка на ней имеет координату у = 0, то точки пересечения графика с осями координат ищутся очень просто. Точка пересечения с осью Оу равна значению функции у(х) при х = 0, т. е. у(0). Точки пересечения с осью Ох являются корнями уравнения у(х) = 0 и называются нулями функции.
Пример 1
Рассмотрим функцию у(х) = -х2 + 6х - 8.
Найдем точки пересечения графика этой функции с осями координат. Чтобы определить точку пересечения графика с осью ординат, вычислим значение функции y(х) при х = 0: у(0) = -02 + 6 · 0 - 8 = -8. Получаем координаты этой точки A(0; -8).
Теперь определим точки пересечения графика данной функции с осью абсцисс. Для этого в функцию у = -х2 + 6х - 8 подставим значение у = 0 и получим квадратное уравнение 0 = -х2 + 6х - 8, или 0 = х2 - 6х + 8.
Решим его: ![]()
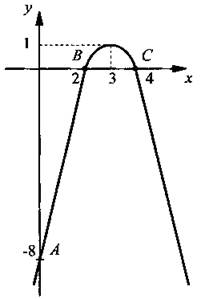
Поэтому график функции пересекает ось абсцисс в двух точках: В(2; 0) и С(4; 0). Для наглядности на рисунке приведен график данной функции (здесь мы несколько забежали вперед).
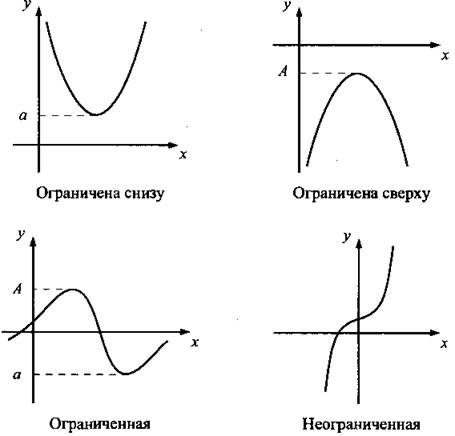
Следующее свойство - ограниченность функции. Функция называется ограниченной снизу, если все значения функции не меньше некоторого числа а (т. е. у(х) ≥ а). Функция называется ограниченной сверху, если все значения функции не больше некоторого числа А (т. е. y(x) ≤ А). Если функция ограничена снизу и сверху, то она называется ограниченной. На рисунке приведены графики ограниченных и неограниченных функций.
Для выяснения ограниченности функции очень часто используются алгебраические преобразования.
Пример 2
Докажем, что функция y(x) = -х2 + 6х - 8 ограничена сверху.
Выделим в функции y(x) = -(x2 - 6х + 8) полный квадрат разности. Для этого в скобках прибавим и вычтем единицу.
Получаем: у(х) = -(х2 - 6х + 8) = -((х2 - 6х + 9) — 1) = -((х - 3)2 - 1) = 1 - (х - 3)2.
Так как при всех значениях х величина (х - 3)2 ≥ 0, величина -(х - 3)2 ≤ 0, то 1 - (х - 3)2 ≤ 1, т. е. у(х) ≤ 1. Тогда по определению данная функция ограничена сверху (при этом число А, входящее в определение, равно 1). Из графика примера 1 наглядно видно, что при всех значениях x значения у(х) ≤ 1.
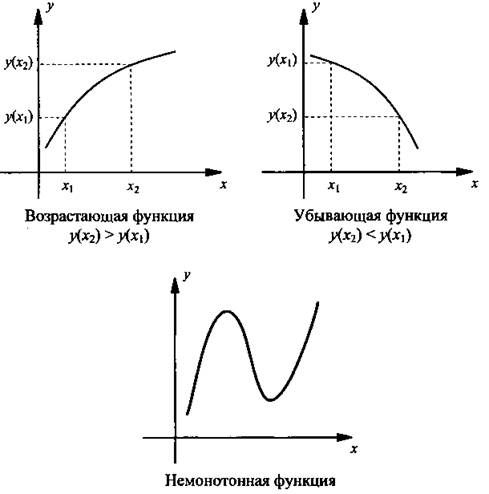
Рассмотрим еще одно свойство функции - монотонность (т. е. возрастание или убывание функции). Функция называется возрастающей, если большему значению аргумента соответствует большее значение функции (т. е. если х2 > х1, то у(х2) > y(x1)). Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции (т. е. если х2 > x1, то у(х2) < y(x1)).
На рисунке приведены графики монотонных (возрастающей и убывающей) и немонотонной функций.
Пример 3
Определить монотонность функции у(х) = -2х + 4.
Область определения этой функции - все значения х, т. е. х ∈ (-∞; +∞). Возьмем два значения х из области определения этой функции х1 и х2 и пусть х2 > х1. Найдем значения функции в этих точках: y(х1) = -2х1 + 4 и у(х2) = -2х2 + 4. Теперь необходимо сравнить эти значения и определить, какое из них больше. Для этого рассмотрим разницу этих величин: у(х2) - y(x1) = (-2х2 + 4) - (-2x1 + 4) = -2х2 + 4 + 2x1 - 4 = -2(х2 – x1).
Так как х2 > x1, то разность х2 – x1 > 0 и величина -2(х2 - x1) < 0. Поэтому получаем: у(х2) - у(x1) < 0, или у(х2) < y(x1). Это неравенство означает, что большему значению аргумента соответствует меньшее значение функции. Поэтому данная функция (по определению) является убывающей. Это же видно из приведенного графика функции.

Функция во всей области определения может быть немонотонной, но на отдельных промежутках функция может быть монотонной. Например, в примере 1 функция в целом немонотонная, но на промежутке х ∈ [3; +∞) функция убывает, а на промежутке х ∈ (-∞; 3] - возрастает (докажите самостоятельно).
И наконец, рассмотрим еще одно свойство функции - четность. Предварительно введем еще одно понятие - симметричность области определения. Область определения называется симметричной, если функция определена и в точке х0, и в точке (-х0) (т. е. в точке, симметричной х0 относительно начала числовой оси).
Пример 4
а) Областью определения функции ![]() являются все значения х, кроме тех, для которых х2 - 4 = 0 (т. е. х = ±2). Поэтому эта функция определена, например, как при х = -1, так и при х = -(-1) = 1.
являются все значения х, кроме тех, для которых х2 - 4 = 0 (т. е. х = ±2). Поэтому эта функция определена, например, как при х = -1, так и при х = -(-1) = 1.
И наоборот, эта функция не определена и при х = -2, и при х = -(-2) = 2. Следовательно, область определения данной функции х ∈ (-∞; -2)U(-2; 2)U(2; +∞) симметричная.
б) Областью определения функции ![]() являются все значения х, кроме тех, для которых х - 4 = 0 (т. е. х = 4). Поэтому эта функция определена в точке x = -4, но не определена в симметричной точке x = -(-4) = 4. Поэтому область определения данной функции x ∈ (-∞; 4)U(4; +∞) не является симметричной.
являются все значения х, кроме тех, для которых х - 4 = 0 (т. е. х = 4). Поэтому эта функция определена в точке x = -4, но не определена в симметричной точке x = -(-4) = 4. Поэтому область определения данной функции x ∈ (-∞; 4)U(4; +∞) не является симметричной.
Понятие четности функции вводится только для функции с симметричной областью определения. Функция называется четной, если при изменении знака аргумента, значение функции не меняется, т. е. y(-х) = у(х). График четной функции всегда симметричен относительно оси ординат.
Функция называется нечетной, если при изменении знака аргумента, значение функции также меняется на противоположное, т. е. у(-х) = -у(х). График нечетной функции всегда симметричен относительно начала координат.
На рисунке приведены (для наглядности) графики четной, нечетной функции и функции, не имеющей никакой четности.

Пример 5
Выяснить четность функций: а) у = |х| - x2; б) у = x - x3; в) y = x - 2.
Прежде всего отметим, что области определения всех трех функций х ∈ (-∞; +∞) симметричны. Для выяснения четности этих функций y(x) надо найти значение y(-x) и сравнить значения y(x) и y(-x).
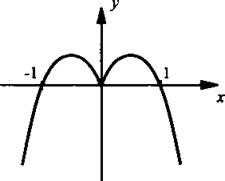
а) y(-x) = |-x| - (-x)2 = |x| - х2 (здесь учтено, что |-х| = |x| и (-х)2 = x2). Теперь легко видеть, что y(-x) совпадает с данной функцией y(x), т. е. y(-x) = y(x). Поэтому данная функция четная и ее график симметричен относительно оси ординат.
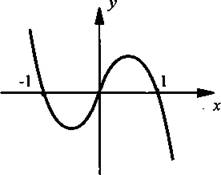
б) y(-х) = -x - (-x)3 = -х - (-х)3 = -х + х3 = -(х - х3) = -у(х). Видно, что значения функции в точках х и -х противоположны по знаку, т. е. y(-x) = -y(x). Поэтому данная функция нечетная и ее график симметричен относительно начала координат.
в) y(-x) = -х - 2. Сравнивая значение –y(x) = -х - 2 со значением y(x) = х - 2, видим, что равенство y(-x) = y(x) не выполняется. Поэтому эта функция не является четной. Найдем теперь величину –y(x) = -(х - 2) = 2 - x. Сравнивая значение y(-x) = -x - 2 со значением –y(x) = 2 - x, видим, что равенство y(-x) = -y(x) также не выполняется. Поэтому эта функция не является нечетной.
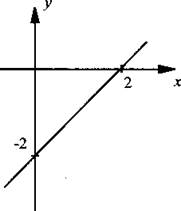
Итак, данная функция никакой четности не имеет и ее график не обладает никакой симметрией.
В заключение отметим, что исследование основных свойств функции облегчает анализ ее поведения и построение ее графика. В старших классах будут рассмотрены и другие свойства функции.
2. Свойства и графики некоторых функций
Теперь необходимо вспомнить основные свойства и графики некоторых ранее изученных функций (свойства надо представлять, но запоминать не стоит).
Линейная функция у = kx + b
1. Область определения - множество всех чисел.
2. Графиком функции является прямая линия.
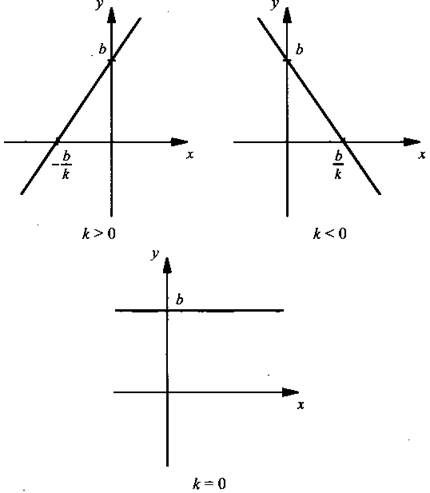
3. График функции пересекает ось абсцисс в точке х = b/k (при k ≠ 0) и параллелен оси абсцисс при k = 0. График функции пересекает ось ординат в точке у = b.
4. Функция возрастает при k > 0, убывает при k < 0 и постоянна при k = 0.
5. Функция неограниченная при k ≠ 0 и ограниченная при k = 0.
6. Функция определенной четности не имеет при b ≠ 0, нечетная при b = 0 и четная при k = 0.
7. Область значений - множество всех чисел при k ≠ 0 и у = b при k = 0.
8. При b = 0 функцию у = kх называют прямой пропорциональностью.
Пример 6
Найти условие, при котором линейная функция у = kх + b является: а) нечетной; б) четной.
Область определения функции х ∈ (-∞; +∞) — симметричная. Найдем значение у(-x) = k · (-х) + b = -kх + b.
а) Если функция нечетная, то у(-x) = -y(x). Получаем: -kх + b = -(kх + b), или b = -b, или 2b = 0, откуда b = 0.
б) Если функция четная, то у(-x) = y(x). Получаем: -kх + b = kх + b, или 0 = 2kх, откуда k = 0 (т. к. x - любое число, не равное нулю).
Обратная пропорциональность у = k/x.
1. Область определения - множество всех чисел, кроме нуля.
2. Графиком функции является гипербола.
3. График функции осей координат не пересекает.
4. Функция возрастает при k < 0 и убывает при k > 0 в области определения.
5. Функция неограниченная.
6. Функция нечетная.
7. Область значений - множество всех чисел, кроме нуля.

Пример 7
Выясним монотонность обратной пропорциональности у = k/x.
Область определения данной функции D(y) = (-∞; 0)U(0; +∞). Рассмотрим два произвольных значения x1 и х2 (где x1 > х2) из области определения функции. Найдем значения функции в этих точках y(x1) = k/x1 и у(х2) = k/x2 и сравним их. Для этого рассмотрим разность 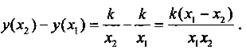 Так как х2 > х1, то разность x1 - х2 отрицательна. Поэтому знак разности у(х2) — у(х1) противоположен знаку дроби k/x1x2.
Так как х2 > х1, то разность x1 - х2 отрицательна. Поэтому знак разности у(х2) — у(х1) противоположен знаку дроби k/x1x2.
Функция у = k/x не определена в точке х = 0. Рассмотрим два промежутка области определения. При х1, х2 ∈ (-∞; 0) и при х1 ,х2 ∈ (0; +∞) произведение x1x2 положительно. Поэтому знак разности у(х2) — у(х1) противоположен знаку коэффициента k. Следовательно, при k < 0 величина у(х2) — у(х1) > 0. т. е. у(х2) > у(х1) и функция возрастает; при k > 0 величина у(х2) — у(х1) < 0, т. е. у(х2) < у(х1) и функция убывает.
Квадратная функция у = х2
Заметим, что функция у = х2 является частным случаем квадратичной функции, которая детально будет изучаться позднее.
1. Область определения - множество всех чисел.
2. Графиком функции является парабола.
3. График функции проходит через начало координат.
4. Функция убывает на промежутке (-∞; 0] и возрастает на промежутке [0; +∞).
5. Функция ограничена снизу, т. е. у ≥ 0.
6. Функция четная.
7. Область значений - промежуток [0; +∞).

Пример 8
Докажем ограниченность квадратичной функции у = х2.
Очевидно, что при всех значениях x величина у = х2 принимает только неотрицательные значения, т. е. у ≥ 0. По определению функция ограничена снизу, т. е. у ≥ а (где а может быть любым неположительным числом: a = -103, a = -5, a = -0,1, a = 0).
Кубическая функция у = x3
1. Область определения - множество всех чисел.
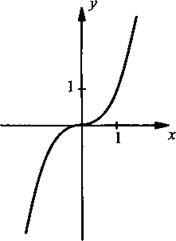
2. График специального названия не имеет.
3. График функции проходит через начало координат.
4. Функция возрастает.
5. Функция неограниченная.
6. Функция нечетная.
7. Область значений - множество всех чисел.
Пример 9
Докажем нечетность кубической функции у = х3.
Область определения функции х ∈ (-∞; ∞) - симметричная. Найдем значение функции у(-х) = (-х)3 = (-1)3 · х3 = -х3 = -y(x). Так как выполнено равенство у(-х) = y(x), то по определению данная функция нечетная.
Функция ![]()
1. Область определения — множество неотрицательных чисел.
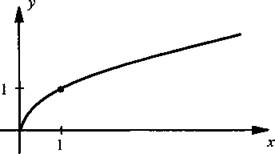
2. График специального названия не имеет.
3. График выходит из начала координат.
4. Функция возрастает.
5. Функция ограничена снизу, т. е. у ≥ 0.
6. Функция определенной четности не имеет.
7. Область значений - множество неотрицательных чисел.
Функция = |x|
1. Область определения - множество всех чисел.
2. График специального названия не имеет.
3. График проходит через начало координат.
4. Функция убывает на промежутке (-∞; 0] и возрастает на промежутке [0; +∞).
5. Функция ограничена снизу, т. е. у ≥ 0.
6. Функция четная.
7. Область значений - множество неотрицательных чисел.
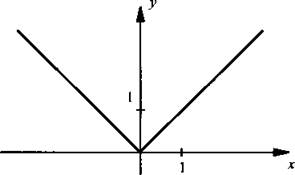
Рассмотренные свойства функций используются и при построении графиков более сложных функций.
Пример 10
Построим график функции ![]()
Область определения функции - множество всех чисел, кроме х = 2. Сократим дробь и запишем функцию в виде ![]()
![]() Поэтому надо построить график линейной функции у = 2 - 2х и удалить из него точку с абсциссой х = 2 (показана стрелками).
Поэтому надо построить график линейной функции у = 2 - 2х и удалить из него точку с абсциссой х = 2 (показана стрелками).
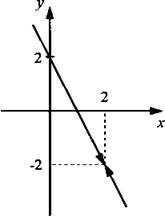
Пример 11
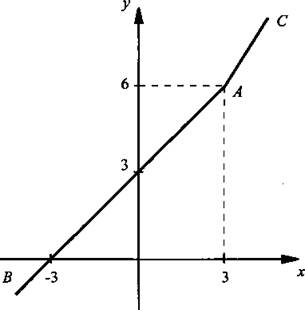
Построим график функции у = 2х + |х - 3|.
Раскроем знак модуля, рассмотрев два случая. При х - 3 < 0 получаем: у = 2х - (х - 3) = х + 3, при x - 3 ≥ 0 имеем: у = 2х + (х - 3) = 3х - 3. Таким образом, надо построить график функции ![]() Строим при х < 3 график прямой у = х + 3 (луч АВ) и при x ≥ 3 график прямой у = 3х - 3 (луч АС). Поэтому графиком данной функции будет ломаная ВАС.
Строим при х < 3 график прямой у = х + 3 (луч АВ) и при x ≥ 3 график прямой у = 3х - 3 (луч АС). Поэтому графиком данной функции будет ломаная ВАС.
IV. Контрольные вопросы
1. Как найти точки пересечения графика функции с осями координат?
2. Понятие ограниченности функции.
3. Возрастающая и убывающая на промежутке функция.
4. Нечетная и четная функции и их свойства.
5. Свойства и график линейной функции y = kх + b.
6. Свойства и график обратной пропорциональности у = k/x.
7. Свойства и график квадратичной функции у = х2.
8. Свойства и график кубической функции y = х3.
9. Свойства и график функции ![]()
10. Свойства и график функции у = |х|.
V. Задание на уроке
№ 17 (а, в); 18 (а); 20; 23; 25 (а); 27; 29 (а); 30 (а, в, д); 31 (а, г); 32; 37; 41 (б); 42 (а); 45; 51 (а); 53 (б); 54 (а).
VI. Задание на дом
№ 17 (б, г); 18 (б); 21; 22; 25 (б); 28; 29 (б); 30 (б, г, е); 31 (б, в); 33; 38; 41 (в); 42 (б); 46 (а); 51 (б); 53 (в); 54 (б, в).
VII. Творческие задания
1. Постройте график функции:
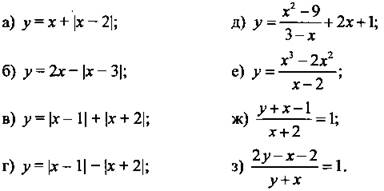
2. Постройте множество точек (х; у), координаты которых удовлетворяют условию:
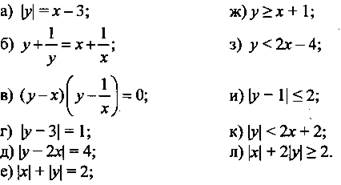
VIII. Подведение итогов урока