Поурочные разработки по Алгебре для 9 класса к учебнику Ю.Н. Макарычева
Дробные рациональные уравнения - Уравнения с одной переменной - Уравнения и неравенства с одной переменной
Цель: решение рациональных уравнений.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
Решите уравнение.
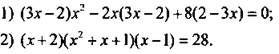
3) При всех значениях параметра а определите число решений уравнения ![]()
Вариант 2
Решите уравнение.
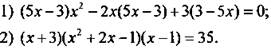
3) При всех значениях параметра а определите число решений уравнения ![]()
III. Изучение нового материала
Уравнение y(x) = 0 называют дробным рациональным уравнением, если выражение у(х) является дробным (т. е. содержит деление на выражения с переменными).
Для решения рационального уравнения его необходимо преобразовать в линейное или квадратное уравнение, решить это уравнение и отбросить те корни, которые не входят в ОДЗ (область допустимых значений) исходного рационального уравнения.
Пример 1
Решить уравнение 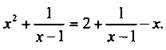
Так как в данное уравнение входит выражение 1/(x - 1), то х - 1 ≠ 0, или х ≠ 1 (что является ОДЗ).
Уравнение принимает вид: х2 = 2 - х или х2 + х - 2 = 0, корни которого x1 = 1 и х2 = -2. Однако х, не является корнем исходного уравнения, поэтому данное уравнение имеет только один корень: х = -2.
Пример 2
Решить уравнение ![]()
ОДЗ уравнения определятся условиями: х ≠ 0 и х ≠ -а. Избавившись от знаменателей в уравнении, например за счет умножения членов уравнения на х(а + х), получим: а + х = х(а - 1). Это уравнение является линейным относительно х и имеет вид: а = х(а - 2). При а - 2 ≠ 0 (т. е. а ≠ 2) корень уравнения ![]() , при а - 2 = 0 (т. е. а = 2) уравнение имеет вид: 2 = х · 0 и корней не имеет. Однако для найденного (при а ≠ 2) корня уравнения
, при а - 2 = 0 (т. е. а = 2) уравнение имеет вид: 2 = х · 0 и корней не имеет. Однако для найденного (при а ≠ 2) корня уравнения ![]() могут существовать такие а, что х = 0 или х = -а, и тогда для таких а исходное уравнение корней иметь не будет.
могут существовать такие а, что х = 0 или х = -а, и тогда для таких а исходное уравнение корней иметь не будет.
Так как ![]() , то для отбора таких а решим уравнения
, то для отбора таких а решим уравнения ![]() Первое уравнение имеет корень а = 0, второе - корни а = 0 и а = 1. Итак, при а = 0 или а = 1 исходное уравнение также корней не имеет. Учитывая все вышесказанное, можно записать ответ: при
Первое уравнение имеет корень а = 0, второе - корни а = 0 и а = 1. Итак, при а = 0 или а = 1 исходное уравнение также корней не имеет. Учитывая все вышесказанное, можно записать ответ: при ![]()
![]() ; при
; при ![]()
При решении рациональных уравнений в основном используются те же приемы, что и при решении алгебраических уравнений, например замена неизвестной.
Пример 3
Решить уравнение ![]()
Легко проверить, что знаменатели дробей не обращаются в ноль. Так как неизвестная х входит в уравнение только в виде комбинации х2 + 2х, то введем замену неизвестной: у = х2 + 2х и получим уравнение ![]() или 5у2 + 13у = 0. Корни этого уравнения у1 = 0, у2 = -13/5. Вернувшись к старой неизвестной х, решим уравнения х2 + 2х = 0 (корни х1 = 0, х2 = -2) и х2 + 2х = -13/5 (корней не имеет).
или 5у2 + 13у = 0. Корни этого уравнения у1 = 0, у2 = -13/5. Вернувшись к старой неизвестной х, решим уравнения х2 + 2х = 0 (корни х1 = 0, х2 = -2) и х2 + 2х = -13/5 (корней не имеет).
Пример 4
Решить уравнение 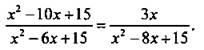
В данном уравнении замена неизвестной не столь очевидна, как в предыдущем. Однако можно заметить, что повторяется комбинация х2 + 15, которую и обозначим у. Тогда получим уравнение ![]() или y2 -21ху + 98х = 0.
или y2 -21ху + 98х = 0.
Заметим также, что должны быть выполнены условия: у ≠ 6х и у ≠ 8х (ОДЗ). Решим теперь уравнение у2 - 21ху + 98х2 = 0 относительно неизвестной у и получим: у = 7х и у = 14х (оба корня удовлетворяют ОДЗ). Возвращаясь к переменной х, имеем уравнения х2 + 15 = 7х (корней не имеет) и х2 + 15 = 14х (корни ![]()
![]() ).
).
Во многих случаях перед заменой неизвестной в уравнении его необходимо преобразовать.
Пример 5
Решить уравнение ![]()
Совершенно не очевидно, какую новую неизвестную можно ввести. Исходя из структуры уравнения, выделим в левой части полный квадрат разности. Для этого вычтем и прибавим выражение 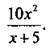 Получаем:
Получаем: ![]() или
или 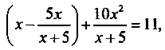 или
или 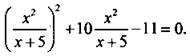 Введем новую переменную
Введем новую переменную ![]() и получим квадратное уравнение у2 + 10у - 11 = 0, корни которого y1 = 1 и у2 = -11. Вернемся к старой переменной. Получаем уравнения:
и получим квадратное уравнение у2 + 10у - 11 = 0, корни которого y1 = 1 и у2 = -11. Вернемся к старой переменной. Получаем уравнения:
а) ![]() или х2 - х - 5 = 0. Корни
или х2 - х - 5 = 0. Корни ![]()
б) ![]() или х2 + 11х + 55 = 0. Уравнение корней не имеет.
или х2 + 11х + 55 = 0. Уравнение корней не имеет.
Предварительные преобразования уравнения позволяют значительно упростить его решение.
Пример 6
Решить уравнение ![]()
![]()
Сначала в обеих частях уравнения выделим целую часть. Для этого в числителе каждой дроби выделим квадрат знаменателя и выполним почленное деление. Получаем: ![]()
![]() или
или ![]()
![]() или
или ![]() Дальнейшие преобразования состоят в получении в каждой части дроби с одинаковыми числителями. Для этого запишем уравнение в виде
Дальнейшие преобразования состоят в получении в каждой части дроби с одинаковыми числителями. Для этого запишем уравнение в виде ![]() или
или ![]() Используем свойство пропорции и получим: х(х2 + 3х + 2) = х(х2 + 7х + 12) или 0 = х(4х + 10). Корни этого неполного квадратного уравнения x1 = 0 и х2 = -2,5 являются также решениями и данного уравнения.
Используем свойство пропорции и получим: х(х2 + 3х + 2) = х(х2 + 7х + 12) или 0 = х(4х + 10). Корни этого неполного квадратного уравнения x1 = 0 и х2 = -2,5 являются также решениями и данного уравнения.
Достаточно часто встречаются рациональные уравнения, содержащие модули.
Пример 7
Решить уравнение 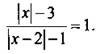
Раскроем знаки модулей, рассмотрев три случая.
а) Если х ≤ 0, получаем уравнение ![]() или -х - 3 = -х + 1. Это уравнение корней не имеет.
или -х - 3 = -х + 1. Это уравнение корней не имеет.
б) Если 0 < х < 2, получаем уравнение ![]() или
или ![]() (при этом х ≠ 1), или х - 3 = 1 - х. Корень этого уравнения х = 2 не входит в рассматриваемый промежуток и не является решением данного уравнения.
(при этом х ≠ 1), или х - 3 = 1 - х. Корень этого уравнения х = 2 не входит в рассматриваемый промежуток и не является решением данного уравнения.
в) Если х ≥ 2, получаем уравнение ![]() или
или ![]() (при этом х ≠ 3). Имеем тождество. Поэтому решением этого уравнения являются промежутки х ∈ [2; 3)U(3; +∞).
(при этом х ≠ 3). Имеем тождество. Поэтому решением этого уравнения являются промежутки х ∈ [2; 3)U(3; +∞).
IV. Задание на уроке
№ 288 (а); 289 (б); 290; 292 (а); 293 (б); 294 (а); 295 (б); 297 (в); 298 (а); 299 (б); 300.
V. Задание а дом
№ 288 (в); 289 (а); 291 (б, в); 292 (б); 293 (а); 294 (б); 295 (а); 297 (б); 298 (б); 299 (а).
VI. Творческие задания
Решите дробно-рациональное уравнение.
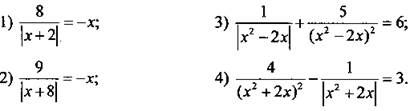
Найдите все значения а, при которых уравнения имеют хотя бы один общий корень. Найдите этот корень.
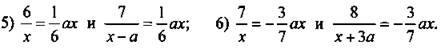
Решите дробно-рациональное уравнение.
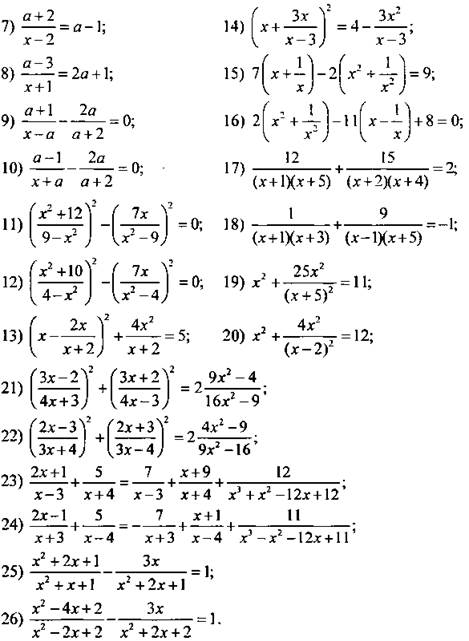
27) Найдите значения параметра а, при которых уравнение ![]() имеет хотя бы одно решение.
имеет хотя бы одно решение.
28) При каких значениях параметров а и b равенство ![]() выполняется для всех допустимых значении х?
выполняется для всех допустимых значении х?
Ответы: ![]()
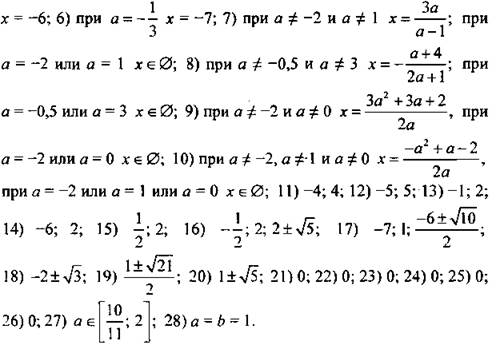
VII. Подведение итогов урока