Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Итоги контрольной работы - урок 10 - МЕТОД ИНТЕРВАЛОВ - КВАДРАТНЫЕ НЕРАВЕНСТВА
Цели: сообщить результаты работы, рассмотреть наиболее типичные ошибки, разобрать трудные задачи.
Ход урока
I. Сообщение темы и цели урока
II. Итоги контрольной работы
1. Распределение работ по вариантам и результатам решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).
№ задачи Итоги |
1 |
2 |
3 |
... |
6 |
+ |
5 |
||||
± |
1 |
||||
— |
1 |
||||
Ø |
1 |
Обозначения:
+ — число решивших задачу правильно или почти правильно.
± — число решивших задачу со значительными ошибками; .
— — число не решивших задачу;
Ø — число не решавших задачу. Вариант 1, 2 — 8 учеников.
2. Типичные ошибки, возникшие при решении задач.
3. Наиболее трудные задачи и их разбор (учителем или школьниками, сделавшими эту задачу).
4. Разбор всей контрольной работы (вывесить на стенде ответы к заданиям вариантов и разбор наиболее трудных вариантов).
III. Ответы и решения
Вариант I
1. Ответ: а) 0 ≤ х ≤ 3; б) х < -3, х > 1/2; в) х — любое число.
2. Ответ: -3 < х < 1.
3. Ответ: а) х ≤ -1, х ≥ 2; б) х ≤ -2, 0 ≤ х < 3.
Вариант 2
1. Ответ: а) х ≤ -4, х ≥ 0; б) -1 < х < 2/3; в) решений нет.
2. Ответ: х < -1, х > 3.
3. Ответ: а) -1 ≤ х ≤ 3; б) -2 ≤ х < 0, х > 3.
Вариант 3
1. Ответ: а) х < -1/3, х > 1/2; б) -1/4 ≤ х ≤ 3/2.
2. Ответ: а) х < -1, х > 2; б) х ≤ -3, -1 ≤ х ≤ 1, х ≥ 3.
3. Ответ: а) -3 ≤ х ≤ -1, х = 2; б) -5 < х ≤ -2, х ≥ 4.
Вариант 4
1. Ответ: а) 1/3 < х < 3/2; б) х ≤ -4, x ≥ 2/3.
2. Ответ: а) -2 < х < 1; б) -4 ≤ х ≤ -2, 2 ≤ х ≤ 4.
3. Ответ: а) х = -1, 2 ≤ х ≤ 3; б) х< -4, 1 ≤ х ≤ 3.
Решения
Вариант 5
1. а). В неравенстве ![]() перенесем число 3 в левую часть и приведем выражения к общему знаменателю:
перенесем число 3 в левую часть и приведем выражения к общему знаменателю: ![]() или
или ![]() Решим это неравенство методом интервалов. Числитель дроби имеет корни х = +3, знаменатель — корень х = -2. Нанесем эти корни на числовую ось и расставим знаки выражения
Решим это неравенство методом интервалов. Числитель дроби имеет корни х = +3, знаменатель — корень х = -2. Нанесем эти корни на числовую ось и расставим знаки выражения ![]() Получаем решение данного неравенства х ≤ -3, -2 < х ≤ 3.
Получаем решение данного неравенства х ≤ -3, -2 < х ≤ 3.

Ответ: х ≤ -3, -2 < х ≤ 3.
б) Раскроем скобки в неравенстве ![]() перенесем все члены в левую часть и приведем подобные члены. Получаем:
перенесем все члены в левую часть и приведем подобные члены. Получаем: ![]() или х2 – 36 > 0. Парабола у = х2 - 36 направлена ветвями вверх и пересекает ось Ох в точках х = ±6. Положительные значения функция y(х) принимает при х < -6 и х > 6.
или х2 – 36 > 0. Парабола у = х2 - 36 направлена ветвями вверх и пересекает ось Ох в точках х = ±6. Положительные значения функция y(х) принимает при х < -6 и х > 6.
Ответ: х < -6, х > 6.
2. Для решения неравенства ![]() построим графики функций y1 = (x + 1)2 (парабола, смещенная на одну единицу влево) и у2 = 1 - |х|. Видно, что значения функции у1 меньше значений функции у2 при -1 < х < 0.
построим графики функций y1 = (x + 1)2 (парабола, смещенная на одну единицу влево) и у2 = 1 - |х|. Видно, что значения функции у1 меньше значений функции у2 при -1 < х < 0.
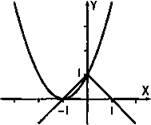
Ответ: -1 < х < 0.
3. Данное выражение имеет смысл при выполнении двух неравенств: x2 – 2x – 35 ≥ 0 и 10 – х > 0. Решение первого неравенства х ≤ -5, х ≥ 7. Решение второго неравенства х < 10. Поэтому оба неравенства выполняются при х ≤ -5, 7 ≤ х < 10.
Ответ: х ≤ -5, 7 ≤ х < 10.
4. а) Для решения неравенства ![]() методом интервалов найдем корни числителя и знаменателя. Для числителя получаем |x - 3| - 2 = 0 или |х - 3| = 2, откуда х - 3 = ±2 и х = 3 ± 2, т. е. х1 = 1 и х2 = 5. Для знаменателя имеем: х2 - 2х - 48 = 0, откуда х3,4 = 1 ±7 , т. е. х3 =- 6 и х4 = 8. Нанесем эти корни на числовую ось и расставим знаки данного выражения в интервалах. Получаем решение неравенства х < -6, 1 ≤ х ≤ 5, х > 8.
методом интервалов найдем корни числителя и знаменателя. Для числителя получаем |x - 3| - 2 = 0 или |х - 3| = 2, откуда х - 3 = ±2 и х = 3 ± 2, т. е. х1 = 1 и х2 = 5. Для знаменателя имеем: х2 - 2х - 48 = 0, откуда х3,4 = 1 ±7 , т. е. х3 =- 6 и х4 = 8. Нанесем эти корни на числовую ось и расставим знаки данного выражения в интервалах. Получаем решение неравенства х < -6, 1 ≤ х ≤ 5, х > 8.

Ответ: х < -6, 1 ≤ х ≤ 5, х > 8.
б) Данное неравенство ах2 - (а + 4)х + 4 > 0 при а = 0 становится линейным -4х + 4 > 0, откуда х > 1. При а ≠ 0 такое неравенство квадратное. Корни квадратного трехчлена 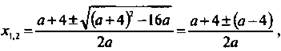 т. е. x1 = 1 и х2 = 4/a. При а < 0 парабола
т. е. x1 = 1 и х2 = 4/a. При а < 0 парабола ![]() направлена ветвями вниз и принимает положительные значения при 4/a < х < 1 (т. к. 4/a < 1). При а > 0 парабола y(x) направлена ветвями вверх. При 0 < a < 4 величина 4/a > 1 и решение неравенства х < 1, х > 4/a. При a = 4 величина 4/a = 1 и решение неравенства х < 1, х > 1. При a > 4 величина 4/a < 1 и решение неравенства х < 4/a, x > 1.
направлена ветвями вниз и принимает положительные значения при 4/a < х < 1 (т. к. 4/a < 1). При а > 0 парабола y(x) направлена ветвями вверх. При 0 < a < 4 величина 4/a > 1 и решение неравенства х < 1, х > 4/a. При a = 4 величина 4/a = 1 и решение неравенства х < 1, х > 1. При a > 4 величина 4/a < 1 и решение неравенства х < 4/a, x > 1.
Учитывая все рассмотренные случаи, получим ответ.
Ответ: при a < 0 4/a < х < 1; при a = 0 х < 1; при 0 < а < 4 х < 1, х > 4/a; при а = 4 х< 1, х > 1; при a > 4 х < 4/a, х > 1.
Вариант 6
1. а) В неравенстве ![]() перенесем число 1 в левую часть и приведем выражения к общему знаменателю:
перенесем число 1 в левую часть и приведем выражения к общему знаменателю: ![]() или
или ![]() или
или ![]() Решим это неравенство методом интервалов. Числитель дроби имеет корни х = 3 (второй кратности), знаменатель — корень х = -4. Нанесем эти корни на числовую ось и расставим знаки выражения
Решим это неравенство методом интервалов. Числитель дроби имеет корни х = 3 (второй кратности), знаменатель — корень х = -4. Нанесем эти корни на числовую ось и расставим знаки выражения ![]() Получаем решение данного неравенства х < -4, х = 3.
Получаем решение данного неравенства х < -4, х = 3.
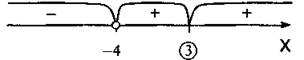
Ответ: х < -4, х = 3.
б) Раскроем скобки в неравенстве ![]() перенесем все члены в левую часть и приведем подобные члены. Получаем:
перенесем все члены в левую часть и приведем подобные члены. Получаем: ![]() или х2 – 81 > 0. Парабола у = х2 - 81 направлена ветвями вверх и пересекает ось Ох в точках х = ±9. Положительные значения функция у(х) принимает при х < -9 и х > 9.
или х2 – 81 > 0. Парабола у = х2 - 81 направлена ветвями вверх и пересекает ось Ох в точках х = ±9. Положительные значения функция у(х) принимает при х < -9 и х > 9.
Ответ: х < -9, х > 9.
2. Для решения неравенства ![]() построим графики функций y1 = (x – 1)2 (парабола, смещенная на одну единицу вправо) и у2 = 1 - |x|. Видно, что значения функции у1 больше значений функции у2 при х < 0 и x > 1.
построим графики функций y1 = (x – 1)2 (парабола, смещенная на одну единицу вправо) и у2 = 1 - |x|. Видно, что значения функции у1 больше значений функции у2 при х < 0 и x > 1.

Ответ: х < 0, x > 1.
3. Данное выражение имеет смысл при выполнении двух неравенств: x2 + 4x – 45 ≥ 0 и 11 – x > 0. Решение первого неравенства х ≤ -9, х ≥ 5. Решение второго неравенства х < 11. Поэтому оба неравенства выполняются при х ≤ -9, 5 ≤ х < 11.
Ответ: х ≤ -9, 5 ≤ х < 11.
4. а) Для решения неравенства ![]() методом интервалов найдем
методом интервалов найдем
корни числителя и знаменателя. Для числителя получаем |х - 2| - 3 = 0 или |х - 2| = 3, откуда х - 2 = ±3 и х = 2 ± 3, т. е. х1 = -1 и х2 = 5. Для знаменателя имеем: х2 + 4х - 21 = 0, откуда х3,4 = -2 ± 5 , т. е. х3 = -7 и х4 = 3 . Нанесем эти корни на числовую ось и расставим знаки данного выражения в интервалах. Получаем решение неравенства -7 < х ≤ -1, 3 < х ≤ 5.

Ответ: -7 < х ≤ -1, 3 < х ≤ 5.
б) Данное неравенство ![]() при а = 0 становится линейным 2х - 2 < 0, откуда х < 1. При а ≠ 0 такое неравенство квадратное. Корни квадратного трехчлена
при а = 0 становится линейным 2х - 2 < 0, откуда х < 1. При а ≠ 0 такое неравенство квадратное. Корни квадратного трехчлена 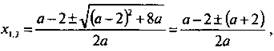 т. е. х1 = 1 и х2 = -2/a. При а < -2 парабола
т. е. х1 = 1 и х2 = -2/a. При а < -2 парабола ![]() направлена ветвями вниз и принимает отрицательные значения при х < -2/a и х > 1 (т. к. -2/a < 1). При а = -2 величина -2/a = 1 и решение неравенства х < 1, х > 1. При -2 < а < 0 величина -2/a > 1 и решение неравенства х < 1, х > -2/a. При а > 0 парабола у(х) направлена ветвями вверх и принимает отрицательные значения при -2/a < х < 1 (т. к. величина -2/a < 1). Учитывая все рассмотренные случаи, получаем ответ.
направлена ветвями вниз и принимает отрицательные значения при х < -2/a и х > 1 (т. к. -2/a < 1). При а = -2 величина -2/a = 1 и решение неравенства х < 1, х > 1. При -2 < а < 0 величина -2/a > 1 и решение неравенства х < 1, х > -2/a. При а > 0 парабола у(х) направлена ветвями вверх и принимает отрицательные значения при -2/a < х < 1 (т. к. величина -2/a < 1). Учитывая все рассмотренные случаи, получаем ответ.
Ответ: при а < -2 х < -2/a, х > 1; при а = -2 х < 1, x > 1; при -2 < a < 0 х < 1, х > -2/a; при а = 0 х < 1; при a > 0 -2/a < х < 1.