Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Общий вид квадратичной функции, ее свойства и график - ФУНКЦИЯ y = ах2 + bх + с - КВАДРАТИЧНАЯ ФУНКЦИЯ
Цель: рассмотреть квадратичную функцию у = ах2 + bх + с и ее свойства, построить график функции.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Как получить из графика функции у = х2 график функции у = 2,5x2 ?
2. Укажите промежутки возрастания функции у = ах2.
3. Парабола у = ах2 проходит через точку (-3; 2). Найти коэффициента.
4. Графически решите неравенство -х2 ≥ -7.
Вариант 2
1. Как получить из графика функции у = х2 график функции у = 1,5х2?
2. Укажите промежутки убывания функции у = ах2.
3. Парабола у = ах2 проходит через точку (-5; 3). Найти коэффициент а.
4. Графически решите неравенство -х2 < -6.
III. Изучение нового материала (основные понятия)
Рассмотрим общий вид квадратичной функции у = ax2 + bх + с, ее свойства и график сначала на частном примере.
Пример 1
Построим график функции у = х2 + 4х + 3.
Составим таблицу значений этой функции в промежутке [-5; 1] с шагом 0,5. Построим эти точки и проведем через них плавную кривую. Получим график данной функции.
x |
-5 |
-4,5 |
-4 |
-3,5 |
-3 |
-2,5 |
-2 |
y |
8 |
5.25 |
3 |
1,25 |
0 |
-0,75 |
-1 |
x |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
|
y |
-0,75 |
0 |
1,25 |
3 |
5,25 |
8 |
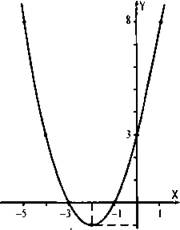
Попросите учащихся отметить закономерности этого графика и сравнить их с графиком функции у = х2.
Укажем эти закономерности:
1. Графиком является парабола, смещенная вдоль оси х и вдоль оси у. Это смещение составляет 2 единицы влево по оси Ох и 1 единицу вниз по оси Оу.
2. Ветви параболы направлены вверх.
3. График симметричен относительно вертикальной прямой с уравнением х = -2.
4. Вершина параболы имеет координаты (-2; -1).
Давайте поймем такое поведение графика функции у = х2 + 4х + 3.
Для этого выделим полный квадрат суммы: у = (х2 + 4х + 3) - 1 или y = (x + 2)2 - 1.

Сначала сравним графики функций у = х2 и y = (x + 2)2. Найдем значение функции у = х2 в точке х1 и получим у1 = x12. Теперь найдем значение второй функции в точки х1 - 2 и получим y = (x1 – 2 + 2)2 = х12. Видно, что значение второй функции совпадает со значением первой функции, но только при значении аргумента на 2 единицы меньше. Так как величина х1 выбрана произвольно, то графиком функции у = (х + 2)2 является парабола, полученная из параболы у = х2 сдвигом (параллельным переносом) влево на 2 единицы.
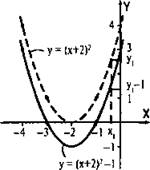
Теперь сравним графики функций y = (x + 2)2 и y = (x + 2)2 - 1. При каждом значении х значение функции y = (х + 2)2 -1 меньше на 1 единицу значения функции у = (х + 2)2. Поэтому графиком функции у = (х + 2)2 -1 является парабола, полученная сдвигом параболы y = (х + 2)2 вниз на 1 единицу.
Следовательно, графиком функции у = х2 + 4х + 3 (или y = (x + 2)2 - 1) является парабола, получаемая сдвигом параболы у = х2 на 2 единицы влево и на 1 единицу вниз. Разумеется, ветви этой параболы направлены вверх. Осью симметрии параболы является прямая, параллельная оси ординат, проходящая через вершину параболы — точку (-2; -1). Таким образом, все отмеченные особенности графика функции у = х2 + 4х + 3 получают объяснение.
Любую квадратичную функцию y = ax2 + bx + c с помощью выделения полного квадрата можно записать в виде ![]() , где величины х0 и y0 выражаются через коэффициенты a, b и с данной функции:
, где величины х0 и y0 выражаются через коэффициенты a, b и с данной функции: ![]()
![]() При этом х0 и y0 — координаты вершины параболы.
При этом х0 и y0 — координаты вершины параболы.
Графиком функции ![]() является парабола, получаемая сдвигом параболы у = ах2:
является парабола, получаемая сдвигом параболы у = ах2:
1) вдоль оси абсцисс вправо, если х0 > 0, и влево, если х0 < 0, на |х0| единиц;
2) вдоль оси ординат вверх, если y0 > 0, и вниз, если у0 < 0, на |у0| единиц. Таким образом, графиком функции у = ах2 + bх + с (или записанной в другом виде функции ![]() ) является парабола, получаемая сдвигом параболы у = ах2 вдоль координатных осей на |x0| и |у0| единиц (см. ранее изложенное). Равенство у = ах2 + bх + с (или
) является парабола, получаемая сдвигом параболы у = ах2 вдоль координатных осей на |x0| и |у0| единиц (см. ранее изложенное). Равенство у = ах2 + bх + с (или ![]() ) называют уравнением параболы.
) называют уравнением параболы.
Координаты (х0 и у0) вершины параболы y = ax2 + bх + с (или ![]() ) можно найти по формулам:
) можно найти по формулам: ![]()
![]() (или
(или ![]() ).
).
Ось симметрии параболы — прямая, параллельная оси ординат и проходящая через вершину параболы, т. е. прямая, имеющая уравнение х = х0.
Ветви параболы направлены вверх, если а > 0, и вниз, если а < 0.
Пример 2
Еще раз вернемся к функции у = х2 + 4х + 3 (пример 1). Для этой функции а = 1, b = 4, с = 3. Найдем координаты вершины параболы ![]()
![]() и
и ![]() (или
(или ![]()
![]() ). Тогда функцию y = x2 + 4x + 3 можно записать в виде
). Тогда функцию y = x2 + 4x + 3 можно записать в виде ![]() или y = 1 · (х - (-2))2 – 1. Поэтому график функции y = x2 + 4x + 3 получается сдвигом графика у = х2 на 2 единицы влево (т. к. х0 = -2 < 0) и на 1 единицу вниз (т. к. у0 = -1 < 0). При этом координаты вершины параболы х0 = -2, у0 = 1; ось симметрии имеет уравнение х = -2. Все эти выводы полностью согласуются с анализом примера 1.
или y = 1 · (х - (-2))2 – 1. Поэтому график функции y = x2 + 4x + 3 получается сдвигом графика у = х2 на 2 единицы влево (т. к. х0 = -2 < 0) и на 1 единицу вниз (т. к. у0 = -1 < 0). При этом координаты вершины параболы х0 = -2, у0 = 1; ось симметрии имеет уравнение х = -2. Все эти выводы полностью согласуются с анализом примера 1.
Пример 3
Написать уравнение параболы, проходящей через точку А(2; 6) и имеющей вершину в точке В(3; 4).
Общее уравнение параболы ![]() , где координаты ее вершины (х0; у0). Так как в данной задаче координаты вершины параболы (3; 4), то уравнение имеет вид у = а(х – 3)2 + 4. Учтем, что парабола проходит через точку А(2; 6) и ее координаты удовлетворяют уравнению параболы. Поэтому получаем: 6 = a(2 – 3)2 + 4 или 6 = а + 4, откуда находим а = 2. Итак, парабола задается уравнением y = 2(x – 3)2 + 4 или у = 2х2 - 12х + 22 .
, где координаты ее вершины (х0; у0). Так как в данной задаче координаты вершины параболы (3; 4), то уравнение имеет вид у = а(х – 3)2 + 4. Учтем, что парабола проходит через точку А(2; 6) и ее координаты удовлетворяют уравнению параболы. Поэтому получаем: 6 = a(2 – 3)2 + 4 или 6 = а + 4, откуда находим а = 2. Итак, парабола задается уравнением y = 2(x – 3)2 + 4 или у = 2х2 - 12х + 22 .
Пример 4
Написать уравнение параболы, проходящей через точки А(-1; 10), В(0; 5) и С(2; 13).
Общее уравнение параболы у = ах2 + bх + с. Так как парабола проходит через три данные точки, то их координаты удовлетворяют уравнению параболы. Получаем систему трех линейных уравнений с тремя неизвестными:  или
или  Подставим значение с = 5 в первое и третье уравнения. Получим систему двух линейных уравнений с двумя неизвестными:
Подставим значение с = 5 в первое и третье уравнения. Получим систему двух линейных уравнений с двумя неизвестными: ![]() или
или ![]() Используя способ сложения, имеем 9 = 3а, откуда a = 3. Тогда из первого уравнения b = a – 5 = 3 – 5 = -2. Итак, найдены коэффициенты а = 3, b = -2 и с = 5. Поэтому уравнение параболы у = 3х2 - 2х + 5.
Используя способ сложения, имеем 9 = 3а, откуда a = 3. Тогда из первого уравнения b = a – 5 = 3 – 5 = -2. Итак, найдены коэффициенты а = 3, b = -2 и с = 5. Поэтому уравнение параболы у = 3х2 - 2х + 5.
IV. Контрольные вопросы
1. В каком виде можно записать квадратичную функцию у = ах2 + bх + с с помощью выделения полного квадрата?
2. Как найти координаты вершины параболы?
3. С помощью каких сдвигов параболы у = ах2 получается график функции ![]() ?
?
4. Какое уравнение имеет ось симметрии параболы ![]() и параболы у = ах2 + bх + с?
и параболы у = ах2 + bх + с?
V. Задание на уроке
№ 608 (1, 3); 609 (1,3); 611 (3,5); 613 (2,4); 615; 616 (1); 617 (1,5); 618 (3); 619 (3); 620.
VI. Задание на дом
№ 609 (2,4); 611 (4, 6); 613 (1, 3); 614; 616 (2); 617 (2, 6); 618 (4); 619 (4).
VII. Творческие задания
1. Написать уравнение параболы, проходящей через точки:
а) А(-1; -2), В(0; -7), С(2; -5).
б) А(-1; 0), В(1; 8), С(2; 29);
в) А(-1; -2), В(0; 2), С(2; 4).
г) А(-1; -6), В(1; 4), С(2; 3).
Ответы: а) у = 2х2 - 3х – 7; б) у = 3х2 + 4х + 1; в) у = -х2 + 3х + 2; г) у = -2х2 + 5х + 1.
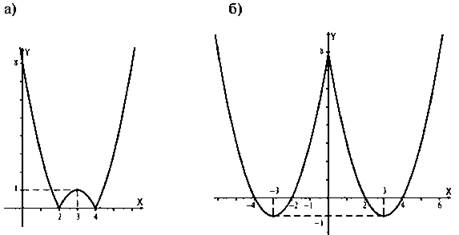
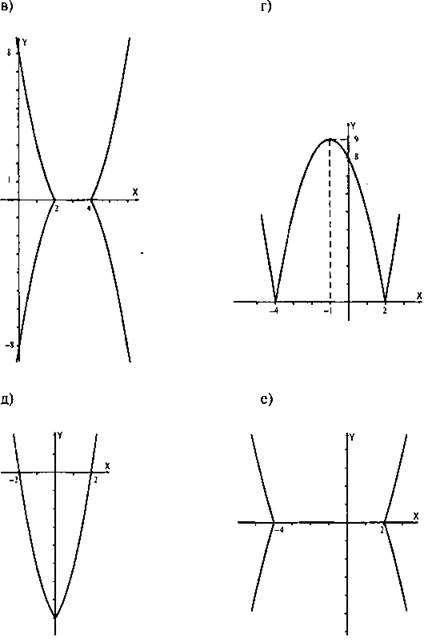
2. Построить график функции или уравнения:

Ответы:
VIII. Подведение итогов урока