Повторение по теме «Квадратные корни» - ПОВТОРЕНИЕ

Цель: напомнить основные понятия и типичные задачи темы.

Ход урока

I. Сообщение темы и цели урока

II. Основные понятия (повторение материала)

Числа, которые используются для счета предметов (1, 2, 3 и т. д.) называют натуральными. К целым числам относятся натуральные числа, противоположные им числа и число 0 (т. е. 0; ±1; ±2; ±3 и т. д.) К рациональным числам относят числа вида m/n (где m — целое число и n — натуральное число), т. е. 3/8; -5; -2/7 и т. д. Рациональное число можно представить в виде конечной десятичной дроби или бесконечной периодической десятичной дроби (например: ). Верно и обратное утверждение: конечную десятичную дробь или бесконечную периодическую десятичную дробь можно представить в виде рационального числа.

Иррациональные числа — бесконечные непериодические десятичные дроби: и т. д. К действительным числам относят рациональные и иррациональные числа.

Модулем числа а называют само число a, если число а неотрицательное, и число -a, если число а отрицательное. Таким образом,

Арифметическим квадратным корнем из неотрицательного числа a называют такое неотрицательное число b, квадрат которого равен а. Таким образом, если b2 = а (при этом а ≥ 0 и b ≥ 0).

Свойства квадратного корня:

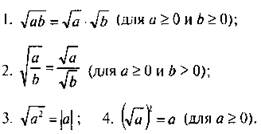
III. Задание на уроке

№ 455 (а, г, и); 458 (г); 462; 468 (а); 474 (д); 481 (а); 487 (в); 491; 499 (а, в).

IV. Задание на дом

№ 455 (б, е, ж); 458 (д); 463; 468 (в); 474 (е); 481 (в); 487 (е); 492; 499 (б, г).

V. Подведение итогов урока