Сложение и вычитание дробей с разными знаменателями - СУММА И РАЗНОСТЬ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цель: изучить сложение и вычитание дробей с разными знаменателями.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Как складываются дроби с одинаковыми знаменателями?

2. Выполните действия:

3. Выделите целую и дробную часть в выражении

Вариант 2

1. Как вычитаются дроби с одинаковыми знаменателями?

2. Выполните действия:

3. Выделите целую и дробную часть в выражении

III. Изучение нового материала (основные понятия)

Сложение и вычитание дробей с разными знаменателями надо свести к сложению и вычитанию дробей с одинаковыми знаменателями. Для этого исходные дроби приводят к общему знаменателю.

Пусть требуется сложить (вычесть) дроби a/b и c/d. Общим знаменателем этих дробей будет произведение bd знаменателей дробей. Приведем данные дроби a/b и c/d к такому общему знаменателю. Для этого умножим числитель и знаменатель первой дроби a/b на дополнительный множитель d и получим Числитель и знаменатель второй дроби c/d умножим на дополнительный множитель b и получим

Теперь можно использовать правило сложения дробей с одинаковыми знаменателями. Имеем: Аналогично можно вычесть дроби с разными знаменателями: .

Пример 1

Сложим и вычтем дроби

Общий знаменатель этих дробей — произведение их знаменателей 4b · 5а = 20ab. Тогда дополнительный множитель к числителю и знаменателю первой дроби 5а, дополнительный множитель к числителю и знаменателю второй дроби 4b. Поэтому получаем:

Пример 2

Сложим дроби

Общий знаменатель этих дробей — произведение их знаменателей Тогда дополнительный множитель к первой дроби 6ab, ко второй дроби 4а2b3. Поэтому получаем: Теперь упростим полученную дробь. Для этого разложим числитель дроби на множители (вынеся общий множитель за скобки) и сократим дробь:

Заметим, что сложение и вычитание дробей с разными знаменателями можно упростить, если приводить дроби не просто к общему знаменателю, а к наименьшему общему знаменателю.

В рассмотренном примере наименьшим общим знаменателем будет одночлен 12а2b4. Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов 4 и 6 дробей. Каждая переменная а и b входит в наименьший общий знаменатель с наибольшим показателем, с которым она входит в знаменатели дробей (соответственно a2 и b4). Дополнительный множитель к первой дроби получим, если разделим наименьший общий знаменатель на знаменатель первой дроби Аналогично, дополнительный множитель ко второй дроби найдем, если разделим наименьший общий знаменатель на знаменатель второй дроби Теперь найдем сумму данных дробей:

Пример 3

Найдем разность дробей

Чтобы найти наименьший общий знаменатель дробей, разложим знаменатель каждой дроби на множители:

Наименьшим общим знаменателем дробей будет выражение аb(а + b). Дополнительный множитель к первой дроби b, ко второй дроби а. Тогда получаем:

Преобразование рационального выражения, которое является суммой или разностью целого выражения и дроби, сводится к нахождению суммы или разности дробей, т. к. любое целое выражение можно представить в виде дроби со знаменателем 1.

Пример 4

Упростим выражение

В данном выражении выделим целое выражение и представим его в виде дроби со знаменателем 1. Выполним вычитание дробей, используя формулу суммы кубов. Тогда получим: .

В некоторых задачах удобно выполнить сложение и вычитание не всех дробей сразу, а выполнять эти операции поочередно.

Пример 5

Докажем, что при любом значении a > 1 значение выражения отрицательно.

Сначала упростим данное выражение, сложив данные дроби. При этом удобно сложить сначала первые две дроби: Теперь к этому результату прибавим третью дробь: Наконец к этой дроби прибавим последнюю четвертую дробь:

Легко сообразить, что при а > 1 (например, при а = 2) и величина a8 > 1. Тогда знаменатель 1 – а8 полученной дроби отрицательный. Так как при этом числитель дроби положительный, то дробь будет отрицательной.

Умение складывать рациональные дроби оказывается полезным и при нахождении сумм обыкновенных дробей.

Пример 6

Найдем сумму дробей

Эта сумма содержит 99 дробей. Поэтому сложить «в лоб» эти дроби очень затруднительно. Тогда представим каждую дробь в этой сумме в виде разности двух более простых дробей.

Каждая дробь в сумме S имеет вид где переменная х принимает значения 1, 2, 3, ..., 98, 99. Очевидно, что дробь может получиться при сложении дробей со знаменателями х и х + 1. Пусть эти дроби имеют числители а и b соответственно. То есть представим дробь в виде Сложим дроби в правой части равенства: В числителе дроби сгруппируем члены, зависяшие от х и не зависящие от х, и получим

Итак, получили, что при всех значениях х должно выполняться равенство Знаменатели дробей в левой и правой части одинаковы. Чтобы числители также были одинаковы при любом значении х, требуется выполнение двух равенств: а + b = 0 и a = 1. Из первого равенства найдем b = -а = -1. Подставим эти значения а и b в равенство и получим (т. е. представили интересующую нас дробь в виде разности двух более простых дробей).

В равенстве вместо х будем поочередно подставлять значения 1, 2, 3, ..., 98, 99 и получим 99 равенств:

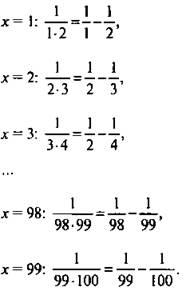
Сложим почленно эти равенства. Тогда в левой части возникает требуемая сумма дробей S. При этом в правой части сократятся все дроби, кроме дробей 1/1 и 1/100. Итак, получаем

Аналогичный прием можно использовать и для нахождения сумм рациональных дробей.

Пример 7

Упростить выражение

Каждое слагаемое в этой сумме имеет вид где n принимает значения n = 0, 2, 4, ..., 98. Представим эту дробь в виде суммы двух более простых дробей с числителями а и b и знаменателями х + n и х + n + 2 соответственно, т. е. Сложим дроби в правой части равенства:

Равенство должно выполняться при любых допустимых значениях х и n. Это возможно, если выполняются равенства: a + b = 0 и 2а = 1.Из последнего равенства найдем a = 1/2, из первого равенства получим b = -a = -1/2.

Подставим эти значения а и b в равенство и получим Таким образом, представили каждую дробь в выражении А в виде разности двух более простых дробей. В это равенство вместо n будем поочередно подставлять значения n = 0, 2, 4, ..., 96, 98 и получим равенства:

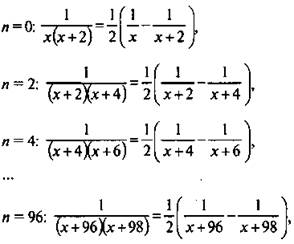
Сложим почленно эти равенства. Тогда в левой части получим данное выражение А. При этом в правой части сокращаются все дроби, кроме дробей Тогда получаем:

IV. Контрольные вопросы

1. Приведение дробей к общему знаменателю. Понятие дополнительного множителя к числителю и знаменателю дроби.

2. Покажите, что сложение и вычитание дробей с разными знаменателями сводится к сложению и вычитанию дробей с одинаковыми знаменателями.

3. Как складываются и вычитаются дроби с разными знаменателями?

4. Сложение (вычитание) целого выражения и дроби.

V. Задание на уроке

№ 70 (а, д); 71 (а, в); 74 (б); 75 (а, б); 76 (а, в); 78 (а, б); 80 (в); 81 (г); 82 (б, г); 84 (а); 87 (б, в); 89 (б); 90 (а, г); 92 (а); 94 (а, г); 96 (б, г); 98 (а); 99(6); 100.

VI. Задание на дом

№ 70 (б, г, е); 71 (б, г)); 72 (а в, д); 74 (а); 75 (г); 76 (г); 78 (в); 80 (а); 81 (в); 82 (а, в); 84 (б); 85 (б); 87 (а, в); 88 (а); 89 (а); 90 (б, в); 92 (б, е); 94 (б, в); 96 (а, в); 97 (а, г); 98 (б); 99 (а); 101.

VII. Творческие задания

1. Найдите а и b из тождества:

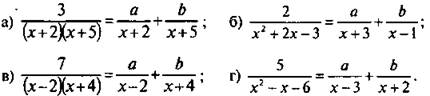
Ответы: a) a = 1, b = -1; б) a = -0,5, b = 0,5 (предварительно убедитесь, что х2 + 2х - 3 = (х + 3)(х - 1); в) а = 7/6, b = -7/6, г) а = 1, b = -1 (убедитесь, что х2 – х – 6 = (х – 3)(х + 2)).

2. Вычислите сумму дробей:

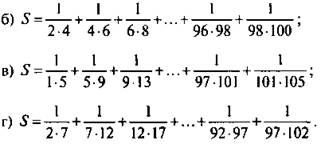
Ответы:

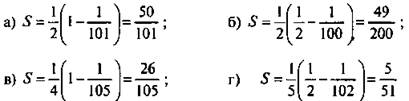(указание: каждую дробь в сумме S представьте в виде разности двух более простых дробей).

3. Упростить выражение:

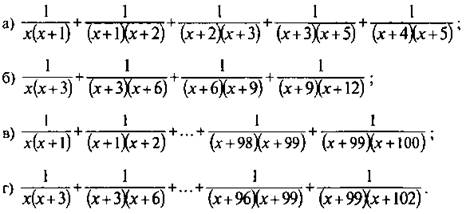
Ответы: (указание: каждую дробь в сумме представьте в виде разности двух более простых дробей).

VIII. Подведение итогов урока