Определение квадратного уравнения. Неполные квадратные уравнения - КВАДРАТНЫЕ УРАВНЕНИЯ И ЕГО КОРНИ - КВАДРАТНЫЕ УРАВНЕНИЯ

Цели: дать определение квадратного уравнения и рассмотреть решение наиболее простых уравнений — неполных квадратных уравнений.

Ход урока

I. Сообщение темы и цели урока

II. Изучение нового материала (основные понятия)

1. Подход к определению квадратного уравнения.

В 7 и 8 классах мы уже рассматривали (и даже решали) квадратные уравнения. Например: а) х2 - 4 = 0; б) 3х2 + 2х = 0; в) х2 - 6х + 8 = 0. Что общего в этих уравнениях? (Члены, содержащие квадрат неизвестной). Также в 7 классе изучались линейные уравнения, например: а) х + 3 = 0; б) 2х = 0; в) 5х + 7 = 0. Чем эти уравнения отличаются от квадратных? (Содержат неизвестную только в первой степени). Вспомните общий вид линейного уравнения и напишите по аналогии общий вид квадратного уравнения (ах2 + bх + с = 0).

2. Определение квадратного уравнения

Уравнение вида ах2 + bx + с = 0 называется квадратным. Здесь х — переменная (неизвестная); а, b и с — некоторые числа (коэффициенты), причем а ≠ 0. При этом число а называют первым коэффициентом (иногда называют и старшим коэффициентом), b — вторым коэффициентом и с — свободным членом. Заметим, что квадратное уравнение называют еще уравнением второй степени, т. к. его левая часть является многочленом второй степени.

Пример 1

Обсудим уравнение (а - 1)х2 + 2ах + 3а + 2 = 0.

Если старший коэффициент а - 1 ≠ 0 (т. е. а ≠ 1), то данное уравнение является квадратным. Если а = 1, то при подстановке этого значения в данное уравнение получаем уравнение 2х + 5 = 0, которое является линейным.

Пример 2

Приведем уравнение (3х + 5)2 = (2x – 3)(2x + 1) к виду ах2 + bх + с = 0.

Используем формулы сокращенного умножения и получим: 9x2 + 30х + 25 = 4х2 - 1. Перенесем все члены уравнения в левую часть: 9х2 + 30х + 25 - 4x2 + 1 = 0 и приведем подобные члены: 5х2 + 30х + 26 = 0. Получили квадратное уравнение, коэффициенты которого равны: а = 5, b = 30 и с = 26.

3. Подход к понятию неполного квадратного уравнения

Рассмотрим квадратные уравнения:

а) 3х2 + 5х + 7 = 0;

б) 2х2 - 6 = 0;

в) 3х2 + 5х = 0.

Чем эти уравнения отличаются друг от друга? (В уравнениях б и в отсутствует один из членов). Как вы решили бы уравнения б и в? (Разложением на множители.)

4. Определение и решение неполного квадратного уравнения

Если в квадратном уравнении ах2 + bх + с = 0 хотя бы один из коэффициентов b и с равен нулю, то такое уравнение называют неполным квадратным уравнением. В случае б) коэффициент b = 0, в случае в) коэффициент с = 0.

В соответствии с определением неполные квадратные уравнения бывают трех видов:

1) ах2 + с = 0 (где с ≠ 0);

2) ах2 + bх = 0 (где b ≠ 0);

3) ах2 = 0.

Пример 3

При каком значении параметра а уравнение 3х2 + (2a + 4)х + а - 3 = 0 является неполным квадратным уравнением?

Так как старший коэффициент данного уравнения равен 3, то оно всегда является квадратным. Такое уравнение будет неполным, если его второй коэффициент или свободный член равны нулю.

Если второй коэффициент равен нулю (т. е. 2а + 4 = 0, откуда а = -2), то уравнение принимает вид 3х2 - 5 = 0 и является неполным квадратным уравнением.

Если свободный член равен нулю (т. е. а - 3 = 0, откуда а = 3), то уравнение имеет вид 3х2 + 10х = 0 и также является неполным квадратным уравнением.

Обсудим решение неполных квадратных уравнений. Основной прием решения таких уравнений — разложение левой части уравнения на множители. В результате решение квадратного уравнения сводится к решению линейных уравнений.

Пример 4

Решим уравнение -5х2 + 15 = 0.

Разделим все члены уравнения на число -5 (не равное нулю) и получим равносильное уравнение х2 - 3 = 0. Учтем, что и по формуле разности квадратов разложим левую часть уравнения на множители: Так как произведение двух множителей равно нулю, то хотя бы один из множителей равен нулю. Получаем два линейных уравнения: (его корень ) и (корень ). Таким образом, данное квадратное уравнение имеет два корня

Аналогично решаются неполные квадратные уравнения вида ах2 + с = 0 (при с ≠ 0). Разделим все члены уравнения на число а (где а ≠ 0) х2 + c/a = 0 и запишем уравнение в виде х2 – (-c/a) = 0. Так как с ≠ 0, то –c/a ≠ 0.

Если –c/a > 0, то представим это число в виде 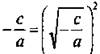и разложим левую часть уравнения на множители по формуле разности квадратов: 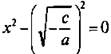или 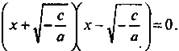Произведение множителей равно нулю, если один из них равен нулю. Получаем два линейных уравнения: (его корень ) и (его корень ). Итак, при –c/a > 0 уравнение ах2 + с = 0 имеет два противоположных по знаку корня

Случай –c/a = 0 не рассматривается, т. к. с ≠ 0.

Если –c/a < 0, то в уравнении х2 – (-c/a) = 0 первый член х2 ≥ 0 при любом значении х, второй член –(-c/a) > 0. Поэтому выражение х2 – (-c/a) > 0 при любом значении х. Следовательно, в этом случае уравнение х2 – (-c/a) = 0 (а также исходное уравнение ах2 + с = 0) не имеет корней.

Теперь рассмотрим неполное квадратное уравнение второго вида.

Пример 5

Решим уравнение 3х2 + 4х = 0.

В левой части уравнения вынесем общий множитель х за скобки и разложим ее на множители: х(3х + 4) = 0. Произведение множителей равно нулю, если один из них равен нулю. Получаем два линейных уравнения: х = 0 (его корень х1 = 0) и 3х + 4 = 0 (корень х2 = -4/3 = ). Итак, данное неполное квадратное уравнение имеет два корня х1 = 0 и х2 = .

Аналогично решаются неполные квадратные уравнения вида ах2 + bх = 0. Разложим левую часть уравнения на множители х(ах + b) = 0. Произведение двух множителей равно нулю, если один из них равен нулю. Получаем два линейных уравнения: х = 0 (его корень х1 = 0) и ax + b = 0 (его корень х2 = -b/a). Итак, неполное квадратное уравнение вида ax2 + bх = 0 (при b ≠ 0) имеет два различных корня х1 = 0 и х2 = -b/a.

Наконец, рассмотрим неполное квадратное уравнение третьего вида ах2 = 0.

Пример 6

Решим уравнение -7х2 = 0.

Разложим левую часть уравнения на множители: -7 · х · х = 0. Так как произведение множителей равно нулю, то хотя бы один из них равен нулю. Очевидно, что число -7 ≠ 0. Поэтому получаем два одинаковых линейных уравнения х = 0 (его корень х = 0). Следовательно, данное уравнение имеет единственный корень (часто говорят, два одинаковых корня) х = 0.

Аналогично решаются неполные квадратные уравнения вида ах2 = 0. Разложим его левую часть на множители: а · х · х = 0. Так как а ≠ 0, то имеем два одинаковых линейных уравнения х = 0 (его корень х = 0). Итак, неполное квадратное уравнение вида ах2 = 0 имеет единственный корень (или два одинаковых корня) х = 0.

Решения неполных квадратных уравнений приведены в таблице.

Вид неполного квадратного уравнения	Корни уравнения
ах2 + с = 0 (где с ≠ 0)	При –c/a > 0
	При –c/a < 0 корней не.
ах2 + bх = 0 (где b ≠ 0)	x1 = 0 и х2 = -b/а
ах2 = 0	х = 0

III. Контрольные вопросы

1. Напишите общий вид квадратного уравнения. Приведите примеры квадратных уравнений.

2. Какое квадратное уравнение называется неполным? Приведите примеры неполных квадратных уравнений.

3. Перечислите три вида неполных квадратных уравнений. Какие корни имеют эти уравнения?

IV. Задание на уроке

№ 504 (б, в, е, устно); 505 (а, г, д, устно); 506 (а, в); 509 (б, д); 511 (а, б); 512 (а, б); 514 (а, в); 515; 518.

V. Задание на дом

№ 504 (а, г, д, устно); 505 (б, в, е, устно); 507 (г); 509 (а, е); 510 (а, в); 513 (а, в); 514 (б, д); 516; 517.

VI. Творческие задания

1. При каких значениях а уравнение является квадратным? Напишите это уравнение.

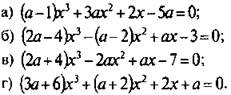
Ответы: а) при а = 1, 3х2 + 2х - 5 = 0 ; б) ни при каких a; в) при a = -2, 4х2 - 2х - 7 = 0; г) ни при каких a.

2. При каких значениях я уравнение является квадратным? При каких значениях я уравнение будет линейным? Напишите это уравнение и решите его.

Ответы: а) при а ≠ 2 — квадратное, при а = 2 — линейное 4х - 5 = 0 (корень );

б) при а ≠ 1 и а ≠ -2 — квадратное, при а = 1 — линейное х - 4 = 0 (корень х = 4), при а = -2 — линейное -2х + 7 = 0 (корень х = 3,5);

в) при а ≠ -1 квадратное, при a = -1i линейное 3х - 3 = 0 (корень х = 1);

г) при а ≠ ±3 квадратное, при а = 3 линейное 6х - 1 = 0 (корень х = 1/6), при а = -3 линейное -6х – 11 = 0 (корень ).

3. При каких значениях а уравнение является неполным квадратным? Напишите это уравнение и решите его.

Ответы: а) при а = 3 2х2 - 15 = 0 (корни ), при а = 0 2х2 + 3х = 0 (корни х1 = 0 и х2 = -1,5);

б) при a = -2 3х2 - 4 = 0 (корни ), при а = 0 3х2 - 4х = 0 (корни х1 = 0 и x2 = );

в) при а = -2 - 3х2 + 6 = 0 (корни ), при a = 0 -х2 + 2х = 0 (корни х1 = 0 и х2 = 2);

г) при а = 19х2 - 4 = 0 (корни х1 = -2/3 и х2 = 2/3), при а = 3 15х2 + 2x = 0 (корни x1 = 0 и х2 = -2/15).

VII. Подведение итогов урока