Поурочное планирование по алгебре 7 класс
Умножение многочлена на многочлен - урок 3 - ІІІ четверть - Многочлены
ЦЕЛЬ УРОКА: Формирование навыка умножения многочлена на многочлен.
ПЛАН УРОКА:
№ |
Этап урока |
Содержание |
Время (мин) |
1 |
Организационный момент |
Нацелить учащихся на урок |
1 |
2 |
Проверка домашнего задания |
Коррекция ошибок |
5 |
3 |
Тренировочные упражнения |
Формировать навык умножения многочлена на многочлен |
21 |
4 |
Самостоятельная работа |
Коррекция ошибок |
15 |
5 |
Подведение итогов урока |
Обобщить теоретические сведения, полученные на уроке |
1 |
6 |
Сообщение домашнего задания |
Разъяснить содержание домашнего задания |
2 |
ХОД УРОКА
I. Организационный момент
II. Проверка домашнего задания (фронтально)
III. Тренировочные упражнения
№№ 700, 702 — на доске и в тетрадях;
№ 788 — самостоятельно под контролем учителя;
№№ 690 (а), 693 (б) — на доске и в тетрадях;
№ 699 (б) — на доске, рассмотрев перед этим пример 3 на с. 137.
IV. Самостоятельная работа
Вариант I
Записать выражение в виде многочлена стандартного вида:
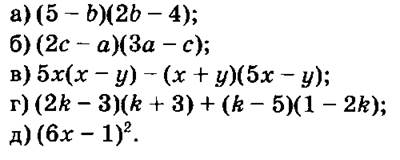
Вариант II
Записать выражение в виде многочлена стандартного вида:
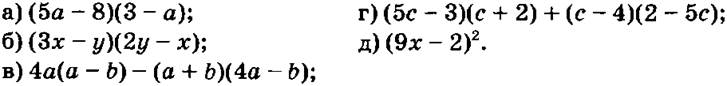
V. Итог урока
VI. Домашнее задание.
п. 29, №№ 690 (б), 698 (в, г), 703, 786
Правило умножения многочленов основано на переместительном и сочетательном свойствах суммы и произведения и на распределительном свойстве умножения. Выводу формулы (а + b)(c + d) = ас + be + ad + bd нужно уделить достаточно внимания, рассматривая и формальный вывод, основанный на замене суммы а + b одной буквой k, и геометрическую иллюстрацию через площадь прямоугольника.
Выполнение заданий п. 29 опирается на знания и умения, сформированные при изучении и освоении теоретического и практического материала предыдущих параграфов.
Для многочленов — целых рациональных функций одного аргумента — можно показать умножение столбиком. Желательно располагать сомножители по убыванию (или возрастанию) степеней «главной буквы» и члены произведения подписывать так, чтобы подобные оказывались в одном столбике.
Например:
1)
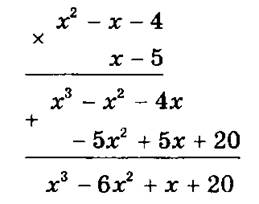
2)
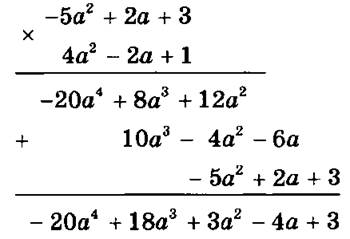
Часть упражнений полезно связать с геометрией; предложив найти выражения для площадей фигур по данным размерам.
Например:
