Умножение многочлена на многочлен - ІІІ четверть - Многочлены

ЦЕЛЬ УРОКА: Формирование умений умножать многочлен на многочлен.

ПЛАН УРОКА:

№	Этап урока	Содержание	Время (мин)
1	Организационный момент	Нацелить учащихся на урюк	1
2	Анализ контрольной работы	Коррекция ошибок	7
3	Устная работа	Актуализировать опорные знания	4
4	Изучение нового материала	Вывести правило умножения многочлена на многочлен	6
5	Тренировочные упражнения	Формировать умение умножать многочлен на многочлен	23
6	Подведение итогов урока	Обобщить теоретические сведения, полученные на уроке	2
7	Сообщение домашнего задания	Разъяснить содержание домашнего задания	2

ХОД УРОКА

I. Организационный момент

II. Анализ контрольной работы. Коррекция ошибок

III. Устная работа

1) Представить в виде многочлена:

2) Выполнить умножение:

3) Какой вид примет выражение За при: а = 5; а = -2; а = b + с?

IV. Изучение нового материала:

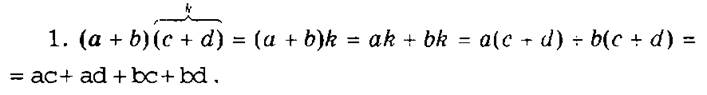
Можно наглядно показать, как идет процесс умножения:

На что умножается член а? Член b (Член а умножается на с и d, т.е. на каждый член второго многочлена).

После этого можно сформулировать правило. Для случая положительных а, b, с, d полученное правило можно проиллюстрировать геометрически. Общая площадь прямоугольника рассматривается как сумма площадей отдельных прямоугольников:

Площадь большого прямоугольника состоит из суммы площадей четырех меньших прямоугольников:

2. Пример:

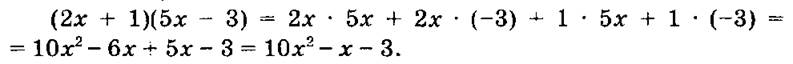
В дальнейшем члены перемножаем сразу, т.е. пишем:

3. Предупреждаем учеников о том, что для того, чтобы не пропустить произведение нескольких членов, нужно сделать подсчет членов произведения: до приведения подобных членов оно равно произведению числа членов одного многочлена на число членов другого.

4. В результате умножения многочлена на многочлен снова получается многочлен, который нужно записать в стандартном виде.

V. Тренировочные упражнения.

№ 677 — на доске и в тетрадях, с подробным комментированием;

№ 678 — в тетрадях, с подробным комментированием;

№ 777 — самостоятельно, с последующей проверкой; обратить внимание на формулировку задания;

№ 680 — на доске и в тетрадях, с подробным комментированием;

№ 683 — самостоятельно, с последующей проверкой.

VI. Итог урока.

Правило умножения многочлена на многочлен

VII. Домашнее задание.

п. 29 (до примера 2), № №679, 681, 684, 706 (а).