Алгебра и начала анализа для учащихся 11 класса поурочные планы
рассмотреть способы решений логарифмических уравнений - РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ - ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ - 2-е полугодие
УРОК № 1
Урок-лекция
Цели: рассмотреть способы решений логарифмических уравнений.
Ход урока
I. Сообщение результатов письменного зачёт.
II. Лекционное изложение нового материала
1. Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим. Простейшим логарифмическим уравнением служит уравнение вида ![]()
2. Решение логарифмического уравнения вида ![]() основано на том, что такое уравнение равносильно уравнению f(х) = g(x) пря дополнительных условиях f(х) > 0, g(x) > 0.
основано на том, что такое уравнение равносильно уравнению f(х) = g(x) пря дополнительных условиях f(х) > 0, g(x) > 0.
3. Проверка найденных значений неизвестного по условию уравнения в общем случае является необязательной. Можно выявить посторонние корни и с помощью нахождения области определения исходного уравнения (эта область задаётся системой неравенств f(х) > 0, g(x) > 0).
4. При решении логарифмических уравнений часто бывает полезен метод введения новой переменной.
5. При решении уравнений, содержащих переменную и в основании, и в показателе степени, используется метод логарифмирования. Если при этом в показателе степени содержится логарифм, то обе части уравнения надо прологарифмировать по основанию этого логарифма.
6. Решите уравнение:
![]()
Решение
![]() Ответ: 7;
Ответ: 7;
![]()
Решение
![]() Ответ: 8.
Ответ: 8.
3) рассмотреть пример 1 на стр. 233 учебника и пример 2 (два способа решения).
4) решить уравнение ![]()
Решение
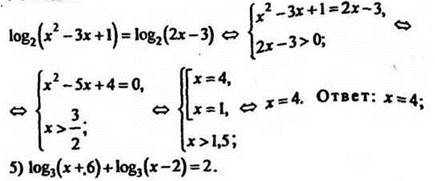
Решение
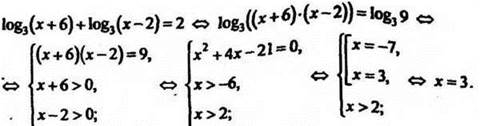
Ответ: х = 3;
6) решить уравнение ![]()
Решение
ОДЗ: х > 0. Обозначим log2х = у, получим ![]()
Если у = -1, тогда ![]() если у = 2, то log2 х = 2; х = 4.
если у = 2, то log2 х = 2; х = 4.
Ответ: 1/4; 4;
7) по учебнику рассмотреть примеры 5 и 7 на стр. 234.
8) Решить уравнение ![]()
Решение
Прологарифмировав обе части уравнения по основанию 2, получим: ![]()
Обозначим log2 x = y, тогда уравнение примет вид у2 + 2у – 3 = 0, откуда y1 = 1, y2 = -3. Значит log2 x = 1 x1 = 2; из уравнения log2 х = -3 находим x2 = 1/8.
Проверка:
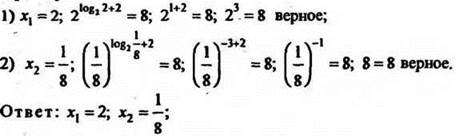
9) решите уравнение ![]()
Решение
Перейдём к одному основанию 5:
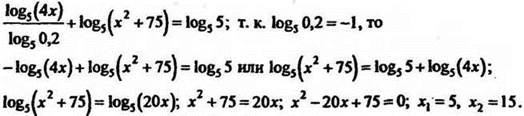
Проверка подтверждает, что значения х1 = 5 и х2 = 15 - корни данного уравнения. Ответ: х = 5; х = 15;
10) решить уравнение ![]()
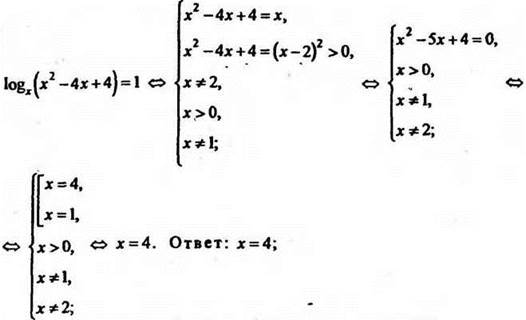
11) самостоятельно разобрать решение примера 3 на стр. 233.
III. Итоги урока
IV. Домашнее задание: п. 39; решить № 512-515, № 519 (в; г) и № 520 (в; г)