Алгебра и начала анализа 10 класс поурочные планы по учебнику Мордковича А. Г.
Преобразования графиков с модулями (факультативное занятие) - Числовые функции - 1-е полугодие
Цель: освоить основные навыки преобразования графиков с модулями.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Как, зная график функции у = f(х), построить график функции у = f(-х) + 2?
2. Постройте график функции:
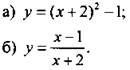
Вариант 2
1. Как, зная график функции у = f(х), построить график функции у = -f(х) - 1?
2. Постройте график функции:
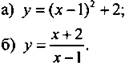
III. Изучение нового материала
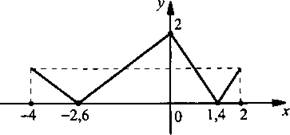
Из материала предыдущего урока видно, что способы преобразования графиков чрезвычайно полезны при их построении. Поэтому рассмотрим также основные способы преобразования графиков, содержащих модули. Эти способы являются универсальными и пригодны для любых функций. Для простоты построения будем рассматривать кусочно-линейную функцию f(х) с областью определения D(f), график которой представлен на рисунке. Рассмотрим три стандартных преобразования графиков с модулями.

1) Построение графика функции у = |f(x)|
f/(x), если Дх)>0,
По определению модуля получим: ![]() Это означает, что для построения графика функции у = |f(x)| надо сохранить часть графика функции у = f(x), для которой у ≥ 0. Ту часть графика функции у = f(х), для которой у < 0, надо симметрично отразить вверх относительно оси абсцисс.
Это означает, что для построения графика функции у = |f(x)| надо сохранить часть графика функции у = f(x), для которой у ≥ 0. Ту часть графика функции у = f(х), для которой у < 0, надо симметрично отразить вверх относительно оси абсцисс.
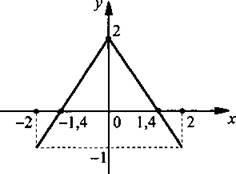
2) Построение графика функции у = f(|x|)
Г/О), если Дх)>0,
Раскроем модуль и получим: ![]() Поэтому для построения графика функции у = f(|x|) надо сохранить часть графика функции у = f(х), для которой х ≥ 0. Кроме того, эту часть надо симметрично отразить влево относительно оси ординат.
Поэтому для построения графика функции у = f(|x|) надо сохранить часть графика функции у = f(х), для которой х ≥ 0. Кроме того, эту часть надо симметрично отразить влево относительно оси ординат.
3) Построение графика уравнения |у| = f(x)
По определению модуля имеем, что при f(х) ≥ 0 надо построить графики двух функций: у = f(х) и у = -f(х). Это означает, что для построения графика уравнения |у| = f(х) надо сохранить часть графика функции у = f(х), для которой у ≥ 0. Кроме того, эту часть надо симметрично отразить вниз относительно оси абсцисс.
Заметим, что зависимость |у| = f(х) не задает функцию, т. е. при х ∈ (-2,6; 1,4) каждому значению х соответствуют два значения у. Поэтому на рисунке представлен именно график уравнения |у| = f(х).
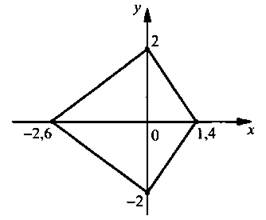
Используем рассмотренные способы преобразования графиков с модулями для построения графиков более сложных функций и уравнений.
Пример 1
Построим график функции ![]()
Выделим в этой функции целую часть ![]()
![]() Такой график получается при смещении графика функции у = -1/x на 2 единицы вправо и на 1 единицу вниз. Графиком данной функции является гипербола.
Такой график получается при смещении графика функции у = -1/x на 2 единицы вправо и на 1 единицу вниз. Графиком данной функции является гипербола.
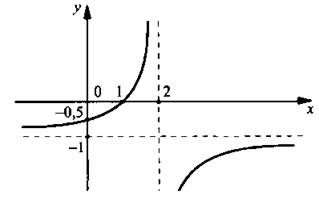
Пример 2
Построим график функции ![]()
В соответствии со способом 1 сохраним часть графика из примера 1, для которой у ≥ 0. Ту часть графика, для которой у < 0, симметрично отразим вверх относительно оси абсцисс.
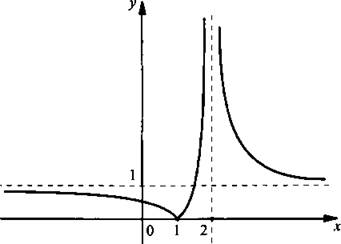
Пример 3
Построим график функции 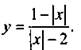
Используя способ 2, сохраним часть графика из примера 1, для которой х ≥ 0. Эту сохраненную часть, кроме того, зеркально отразим влево относительно оси ординат. Получим график функции, симметричный относительно оси ординат.

Пример 4
Построим график уравнения ![]()
В соответствии со способом 3 сохраним часть графика из примера 1, для которой у ≥ 0. Кроме того, эту сохраненную часть симметрично отразим вниз относительно оси абсцисс. Получим график данного уравнения.
Разумеется, рассмотренные способы преобразования графиков можно использовать и совместно.
Пример 5
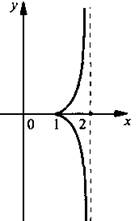
Построим график функции 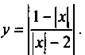
Используем график функции 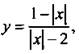 построенный в примере 3. Чтобы построить данный график, сохраним те части графика 3, для которых у ≥ 0. Те части графика 3, для которых у < 0, симметрично отразим вверх относительно оси абсцисс.
построенный в примере 3. Чтобы построить данный график, сохраним те части графика 3, для которых у ≥ 0. Те части графика 3, для которых у < 0, симметрично отразим вверх относительно оси абсцисс.

В тех случаях, когда модули входят в зависимость иным образом (чем в способах 1-3), необходимо эти модули раскрыть.
Пример 6
Построим график функции ![]()
Выражения х - 1 и x + 2, входящие под знаки модулей, меняют свои знаки в точках х = 1 и x = -2 соответственно. Отметим эти точки на координатной прямой. Они разбивают ее на три интервала. Используя определения модуля, раскроем модули в каждом промежутке.
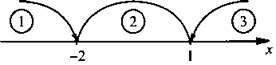
Получим:
1. При ![]()
2. При ![]()
3. При ![]()
Построим графики этих функций, учитывая интервалы для переменной х, в которых раскрывались знаки модуля. Получим ломаную прямую.
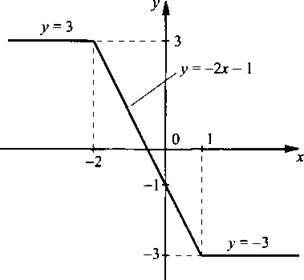
Достаточно часто при построении графиков уравнений с модулями для их раскрытия используют координатную плоскость. Поясним это следующим примером.
Пример 7
Построим график уравнения ![]()
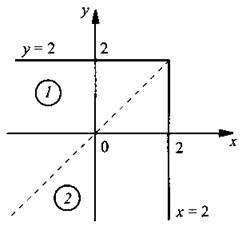
Выражение у - х меняет свой знак на прямой у = х. Построим эту прямую - биссектрису первого и третьего координатных углов. Эта прямая разбивает точки плоскости на две области: 1 - точки, расположенные над прямой у – х; 2 - точки, расположенные под этой прямой. Раскроем модуль в таких областях. В области 1 возьмем, например, контрольную точку (0; 5). Видим, что для этой точки выражение у - х > 0. Раскрывая модуль, получим: у - х + у + х = 4 или y = 2. Строим такую прямую в пределах первой области. Очевидно, в области 2 выражение у - х < 0. Раскрывая модуль, имеем: -(у - х) + у + х = 4 или х = 2. Строим эту прямую в пределах области 2. Получаем график данного уравнения.
IV. Контрольные вопросы
1. Как, используя график функции у = f(х), построить график функции у = |f(х)|?
2. С помощью графика функции у = f(х) постройте график функции y = f(|x|).
3. Как с помощью графика функции у = f(x) построить график уравнения |у| = f(х)?
V. Задание на уроке
§ 1, № 12 (а, б); 15 (а, в).
VI. Задание на дом
§ 1, № 12 (в, г); 15 (б, г).
VII. Творческие задания
1. Постройте график линейной функции и уравнения:
![]()

2. Постройте график квадратичной функции и уравнения:
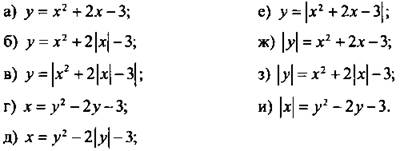
3. Постройте график дробно-линейной функции и уравнения:

4. Постройте график функции, уравнения, неравенства:
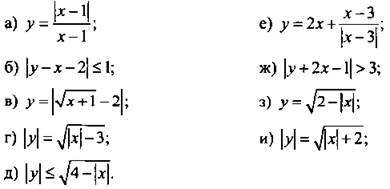
VIII. Подведение итогов урока