Контрольная работа по теме Неравенства и системы неравенств - Рациональные неравенства и их системы

Цель: проверить знания учащихся с использованием разноуровневых вариантов.

Ход уроков

I. Сообщение темы и цели уроков

II. Характеристика контрольной работы

Контрольная работа составлена в шести вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 - сложнее и варианты 5, 6 - самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

При проверке вариантов 1, 2 оценка “5” ставится за правильное решение пяти задач, оценка “4” - четырех задач и оценка “3” - трех задач. Одна задача является резервной (или запасной) и дает некоторую возможность выбора учащимся. При таких же критериях оценки в случае вариантов 3, 4 дается дополнительно 0,5 балла и в случае вариантов 5, 6 - дополнительно 1,0 балла (учитывая более высокую сложность этих вариантов). Поэтому в случае вариантов 5, 6 оценку “5” можно получить за правильное решение четырех задач.

Выбор вариантов может быть сделан учителем или учащимся (при этом количество вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.

III. Варианты работы

Вариант 1

1. Решите неравенство:

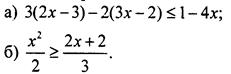
2. Решите систему неравенств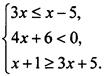

3. При каких значениях переменной имеет смысл выражение

4. Решите неравенство |2х - 1| ≤ 3.

5. При всех значениях параметра а решите неравенство (а - 2)х > а² - 4.

Вариант 2

1. Решите неравенство:

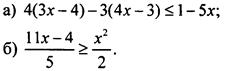
2. Решите систему неравенств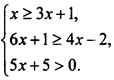

3. При каких значениях переменной имеет смысл выражение

4. Решите неравенство |2х + 1| ≤ 5.

5. При всех значениях параметра а решите неравенство (a + 3)х < а² - 9.

Вариант 3

1. Решите неравенство:

2. Решите систему неравенств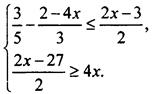

3. При каких значениях переменной имеет смысл выражение

4. Решите неравенство

5. При всех значениях параметра а решите неравенство х² - 3ах + 2а² ≤ 0.

Вариант 4

1. Решите неравенство:

2. Решите систему неравенств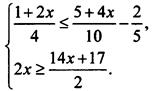

3. При каких значениях переменной имеет смысл выражение

4. Решите неравенство

5. При всех значениях параметра я решите неравенство х² - 4ах + 3а² ≥ 0.

Вариант 5

1. Какие значения может принимать переменная у, если 3х + 2у = 6 и |х| ≤ 8?

2. Решите неравенство

3. Решите неравенство

4. При каких значениях параметра а система неравенств имеет ровно три целых решения?

5. Найдите все пары (х; у) чисел х и у, для которых выполнено неравенство (х² - 4х + 7)(у² + 2у + 10) ≤ 27.

6. При всех значениях параметра а решите неравенство х² - (3а + 1)х + 2а² + 2а ≥ 0.

Вариант 6

1. Какие значения может принимать переменная х, если 4х + 3у = 8 и |у| ≤ 12?

2. Решите неравенство

3. Решите неравенство

4. При каких значениях параметра а система неравенств имеет ровно три целых решения?

5. Найдите все пары (х; у) чисел х и у, для которых выполнено неравенство (х² - 2х + 9)(у² + 4у + 7) ≤ 24.

6. При всех значениях параметра а решите неравенство х² - (3а + 1)х + 2а² + а ≤ 0.