Простейшие вероятностные задачи - Элементы комбинаторики, статистики и теории вероятностей

Цель: рассмотреть простейшие понятия теории вероятностей.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Определение среднего арифметического.

2. Приведен рост (в сантиметрах) пяти человек: 163, 183, 172, 180, 172. Найдите среднее, моду, медиану.

Вариант 2

1. Определение моды измерений.

2. Приведен рост (в сантиметрах) пяти человек: 187, 162, 171, 162, 183. Найдите: среднее, моду, медиану.

III. Изучение нового материала

В классической математике работают с реальной моделью ситуации (например, встреча двух пешеходов), которая однозначно описывается с помощью математического аппарата. В жизни мы постоянно сталкиваемся с тем, что некоторое событие может произойти, а может и не произойти (например, не оговоренная заранее встреча двух друзей в кафе). Такие непредсказуемые события называют случайными. Теория вероятностей изучает различные модели случайных событий, их свойства и характеристики. Разумеется, эта теория не может однозначно предсказать, какое событие в реальности произойдет, но может оценить, какое событие наиболее вероятно. Естественно, как и во всей остальной математике, выбранная модель идеализирована (например, смеси веществ считаются идеально перемешанными, изменение скорости тела происходит мгновенно и т. д.). Поэтому, как мы наблюдаем в жизни, почти небывалое событие происходит, а ожидаемое - нет.

Теперь разберемся с основными понятиями теории вероятностей. При этом будем считать, что случайные события равновероятны (или равновозможны), - идеализированная модель.

Классическое определение вероятности. Вероятностью события А при проведении некоторого испытания называют отношение числа тех исходов, в результате которых наступает событие А, к общему числу всех (равновозможных между собой) исходов этого испытания.

Для решения задач используют алгоритм нахождения вероятности случайного события. Необходимо определить:

1) число N всех равновозможных исходов данного испытания;

2) количество N(A) исходов, в которых наступает событие А;

3) частное равняется вероятности события А, которое обозначают символом Р(А), т. е.

Пример 1

Найдем вероятность того, что при одном бросании игральной кости (кубика) выпадет: а) три очка; б) число очков, кратное трем; в) число очков больше трех; г) число очков, некратное трем.

Всего имеется N = 6 возможных исходов: выпадение 1, 2, 3, 4, 5, 6 очков. Считаем, что эти исходы равновозможны.

а) Только при одном из исходов N(A) = 1 происходит интересующее нас событие А - выпадение трех очков. Вероятность этого события

б) При двух исходах N(B) = 2 происходит событие В: выпадение числа очков, кратных трем: выпадение или трех, или шести очков. Вероятность такого события

в) При трех исходах N(C) = 3 происходит событие С: выпадение числа очков больше трех: выпадение 4, 5 или 6 очков. Вероятность этого события

г) Из шести возможных выпавших чисел четыре (1, 2, 4 и 5) некратны трем, а остальные два (3 и 6) делятся на три. Значит, интересующее нас событие D наступает в четырех случаях, т. е. N(D) = 4. Вероятность такого события

Пример 2

Найдем вероятность того, что при вытаскивании одной карты из колоды (52 карты) эта карта окажется: а) дамой пик; б) дамой любой масти; в) картой пиковой масти; г) картой черной масти.

Всего имеется N = 52 возможных исхода. Считаем, что эти исходы равновероятны.

а) Очевидно, что в колоде только одна дама пик. Поэтому только при одном из исходов N(A) = 1 происходит интересующее нас событие А - выпадение дамы пик. Вероятность этого события

б) Также в колоде имеются карты четырех мастей, в том числе четыре дамы. Поэтому при четырех исходах N(B) = 4 происходит нужное нам событие В - выпадение любой дамы. Вероятность такого события

в) В колоде имеется по 13 карт каждой масти, в том числе и пиковой. Поэтому число интересующих нас исходов N(C) = 13 - выпадение карты пиковой масти. Вероятность этого события

г) В колоде имеется 26 карт черной масти и 26 карт красной масти. Число интересующих нас исходов N(D) = 26 - выпадение карты черной масти. Вероятность такого события

Событие, которое происходит всегда, называют достоверным событием. Например, событие, состоящее в том, что при бросании игральной кости выпадет натуральное число очков. Вероятность достоверного события равна 1. Событие, которое не может произойти, называют невозможным, например выпадение 9 очков на игральной кости. Вероятность невозможного события равна 0. Таким образом, вероятность Р(А) некоторого события 0 ≤ Р(А) ≤ 1.

При решении некоторых задач удобно использовать свойство вероятностей противоположных событий. События А и В называют противоположными, если всякое наступление события А означает ненаступление события В, а ненаступление события А - наступление события В. Событие, противоположное событию А, обозначают символом . Сумма вероятностей противоположных событий равна 1, т. е.

Пример 3

Пусть бросают игральную кость. Обозначим события: А - выпадения четного числа очков, В - выпадение нечетного числа очков. Очевидно, что А и В - противоположные события, т. е. При этом

Пример 4

Бросают две игральные кости. Какова вероятность того, что сумма очков, выпавших на двух кубиках, меньше 10?

Общее число равновозможных исходов этого испытания равно 36. Пусть событие А означает, что сумма выпавших на двух кубиках очков меньше 10. Так как благоприятным для события А является большое число исходов, то удобно сначала найти вероятность противоположного ему события , которое означает, что сумма выпавших очков больше или равна 10. Благоприятными для события являются: 6 + 4; 6 + 5; 6 + 6; 5 + 6; 4 + 6. Поэтому вероятность

Отметим основное правило, используемое в теории вероятностей: правило сложения вероятностей.

Два события называют несовместными, если в одном и том же испытании они не могут произойти одновременно, т. е. наступление одного из них исключает наступление другого.

Пример 5

Пусть в мешке находятся 15 шаров: 7 белых, 5 красных и 3 зеленых. Из мешка наугад вынимают один шар.

Рассмотрим следующие события: событие А - шар оказался красным; событие В - шар оказался зеленым (очевидно, что события А и В несовместны); событие С - шар оказался не белым (красным или зеленым). Выясним, как вероятность события С связана с вероятностями каждого из событий А и В.

Найдем вероятности событий А, В, С. Для каждого испытания (извлечение из мешка одного шара) равновозможными являются 15 исходов. Из них для события А благоприятны 5 исходов, для события В - 3 исхода, для события С - 8 исходов. Находим вероятности этих событий: Видно, что Р(С) = Р(А) + Р(В).

Имеем правило сложения вероятностей: если событие С означает, что наступает одно из двух несовместных событий А или В, то вероятность события С равна сумме вероятностей событий А и В.

Во многих случаях количество всех исходов и интересующих нас исходов бесконечно. Поэтому понятие классической вероятности использовать невозможно.

Вероятность случайного события иногда можно найти, используя геометрические соображения (геометрическая вероятность).

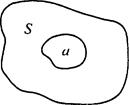
Предположим, что точку бросают в фигуру площади S. Пусть эта фигура содержит фигуру площади а. Будем считать вероятностью Р попадания точки в меньшую фигуру отношение a/S, т. е. Р = a/S.

Пример 6

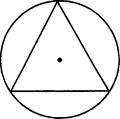
В окружность вписан правильный треугольник. Найдем вероятность того, что точка, брошенная в круг, попадет в треугольник.

Пусть радиус окружности равен R, а сторона треугольника равна с. Свяжем между собой эти переменные. Используем теорему синусов: откуда Найдем площадь треугольника: Найдем вероятность попадания точки в треугольник:

Пример 7

Коля и Миша договорились встретиться в условленном месте с 10 ч до 10 ч 30 мин, причем каждый пришедший ждет другого 10 мин, после чего уходит. Найдем вероятность того, что встреча состоится, если каждый выбирает момент своего прихода наудачу в указанном интервале.

Пусть х - момент прихода на место встречи Коли, у - момент прихода Миши. Так как время ожидания составляет 10 мин, то для встречи необходимо выполнение неравенства |у - x| ≤ 10, или -10 ≤ у - х ≤ 10, или х - 10 ≤ у ≤ х + 10. На координатной плоскости построим квадрат со стороной 30. Каждая точка этого квадрата соответствует времени прихода мальчиков.

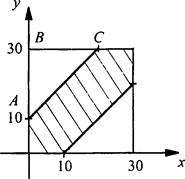
Построим также множество точек, удовлетворяющих неравенству х - 10 ≤ y ≤ х + 10 (эта область заштрихована). Тогда вероятность встречи мальчиков равна отношению площади заштрихованной фигуры к площади квадрата. Площадь квадрата равна 30² = 900. Найдем площадь треугольника АВС и получим: Тогда площадь заштрихованной фигуры: 900 - 2 ∙ 200 = 500. Вероятность встречи мальчиков

IV. Контрольные вопросы

1. Понятие вероятности события.

2. Какие события называют несовместными?

3. Правило сложения вероятностей.

4. Свойство вероятностей противоположных событий.

5. Понятие о геометрической вероятности.

V. Задание на уроках

§ 20, № 1; 3; 6; 9; 11 (а, б); 12 (а, в); 15; 18; 21 (а, б); 22 (а, г).

VI. Задание на дом

§ 20, № 2; 5; 7; 10; 11 (в, г); 12(б, г); 16; 19; 21 (в, г); 22 (б, в).

VII. Подведение итогов уроков