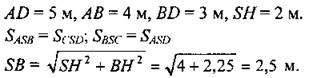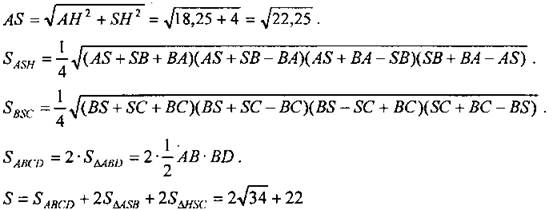Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ПИРАМИДА - НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ СТЕРЕОМЕТРИИ
|
Цели деятельности учителя |
Создать условия для ознакомления учащихся с пирамидой (ее основания, боковые грани, вершины пирамиды, боковые ребра пирамиды), определением правильной пирамиды, апофемы пирамиды, для выведения формулы объема пирамиды; способствовать развитию логического мышления |
||
|
Термины и понятия |
Пирамида, грани, ребра, правильная пирамида, апофема, объем пирамиды, тетраэдр |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют объяснять, какой многоранник является пирамидой, что такое основание, апофема, какая пирамида называется правильной |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации. Регулятивные: умеют устанавливать причинно-следственные связи, строить логические рассуждение, делать умозаключения и формулировать выводы. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Модели пирамид |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Выявить уровень сформированности теоретических знаний учащихся |
(Ф) - Что называется призмой? прямой призмой? правильной призмой? - Объясните, что такое параллелепипед? Дайте определение прямого параллелепипеда, прямоугольного параллелепипеда. - Сформулируйте свойство четырех диагоналей параллелепипеда. - Сформулируйте основные свойства объемов. - Что такое измерения прямоугольного параллелепипеда? - Сформулируйте свойство диагонали прямоугольного параллелепипеда. - Чему равен объем куба? Объем прямоугольного параллелепипеда? - Какой формулой выражается объем призмы? Проверка решения задачи № 1196 |
||
|
II этап. Учебно-познавательная деятельность |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Ввести понятие пирамиды, научить ее строить; записать формулу для нахождения объема пирамиды |
(Ф/И) 1. Учащиеся самостоятельно изучают материал пункта 128 “Пирамида” по учебнику (с. 311-313). 2. Учитель на моделях различных пирамид объясняет учащимся, что такое пирамида, основание пирамиды, боковые грани пирамиды, вершина пирамиды, боковые ребра пирамиды. 3. Вводится новое понятие: треугольную пирамиду часто называют тетраэдром. 4. На доске и в тетрадях строятся изображения пирамиды; проводятся высота пирамиды и апофема (рис. 353). 5. В тетрадях учащиеся записывают определения: а) Отрезок, соединяющий вершину пирамиды с плоскостью ее основания и перпендикулярный к этой плоскости, называется высотой пирамиды. б) Пирамида называется правильной, если ее основание - правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. в) Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. 6. Вводится формула: объем пирамиды равен одной трети произведения площади основания на высоту: |
||
|
III этап. Решение задач |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Совершенствовать навыки решения задач |
(Ф/И) Организует работу учащихся. 1. Решить задачу № 1201, используя модель тетраэдра (устно). 2. Решить задачу № 1202 (а) на доске и в тетрадях. 3. Решить задачу № 1203 самостоятельно. (Затем по готовому чертежу на доске проверяется построение сечения). 4. Решить задачу № 1204. (Решение объясняет учитель, привлекая учащихся к обсуждению построения сечения.) 5. Решить задачу № 1206. 6. Решить задачу № 1241 |
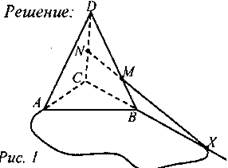
№ 1201. Нет. № 1202.
Решение: Прямая MN принадлежит плоскости BCD, которая пересекается с плоскостью АВС по ВС. Продолжим ВС до пересечения с прямой MN в точке X. Точка Х принадлежит и прямой MN, и плоскости АВС, так как точка X лежит на прямой ВС, принадлежащей плоскости АВС. № 1203.
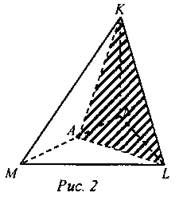
Решение: По условию МА = NA. Проводим отрезок AL, так как точки L и Aпринадлежат одной плоскости MNL. Проводим отрезок АК, так как точки К и А принадлежат одной плоскости MKN. Искомое сечение - треугольник AKL. № 1204.
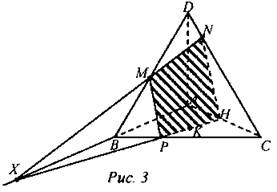
Решение: 1) Проводим прямую MN, продолжаем АВ до пересечения с прямой MN в точке X. 2) Точка X принадлежит плоскости АВС, и точка К принадлежит плоскости АВС, тогда проводим прямую ХК, пересекающую прямые ВС и АС в точках Р и Н соответственно. 3) Проводим отрезки МР, NH и PH. Четырехугольник PMNH - искомое сечение. № 1206. Решение: Найдем сумму площадей боковых граней правильной пирамиды. Так как гранями боковыми правильной пирамиды являются равные равнобедренные треугольники и площадь треугольника равна, то сумма площадей всех треугольников равна
Значит, площадь боковой поверхности правильной пирамиды равна: № 1241.
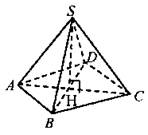
Решение:
В ∆ABD: AD2 = AB2 + BD2, следовательно, он прямоугольный с прямым углом ABD. Из ∆АВН по теореме Пифагора:
|
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Оцените свою работу на уроке. - Что для вас оказалось наиболее сложным? - Задайте три вопроса по теме урока |
(И) Домашнее задание: изучить материал пункта 128; повторить пункты 122-127; ответить на вопросы 1-14 в учебнике на с. 327; решить задачи № 1202 (б), 1211 (а), 1207 |
||