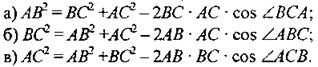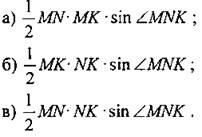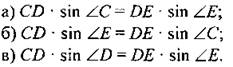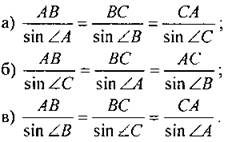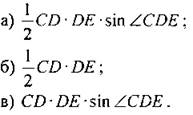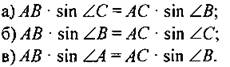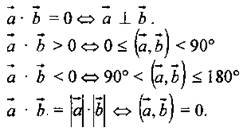Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Цель деятельности учителя

Создать условия для ознакомления учащихся с понятием “угол между векторами”, введения понятий скалярного произведения двух векторов, скалярного квадрата

Термины и понятия

Косинус, угол между векторами, скалярное произведение, скалярный квадрат

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом по основным разделам содержания

Познавательные: умеют понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий.

Регулятивные: принимают и сохраняют учебные задачи.

Коммуникативные: умеют участвовать в диалоге.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Тест

I этап. Тест

Цель деятельности

Задания для самостоятельной работы

Проверить уровень усвоения теоретических знаний

(И) Тест с самопроверкой.

Вариант I

1. Для треугольника справедливо равенство:

2. Площадь треугольника MNK равна:

3. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то эта сторона лежит против:

а) тупого угла;

б) прямого угла;

в) острого угла.

4. В треугольнике АВС известны длины сторон АВ и ВС. Чтобы найти сторону АС, необходимо знать величину:

а) угла A;

б) угла В;

в) угла С.

5. Треугольник со сторонами 5, 6 и 7 см:

а) остроугольный;

б) прямоугольный;

в) тупоугольный.

6. В треугольнике АВС ∠А = 30°, ВС = 3. Радиус описанной около ААВС окружности равен:

а) 1,5;

б) 2√3;

в) 3.

7. Если в треугольнике АВС ∠А = 48°, ∠B = 72°, то наибольшей стороной треугольника является сторона:

а) АВ:

б) АС:

в) ВС.

8. В треугольнике CDE:

9. По теореме синусов:

а) стороны треугольника обратно пропорциональны синусам противолежащих углов;

б) стороны треугольника пропорциональны синусам противолежащих углов;

в) стороны треугольника пропорциональны синусам прилежащих углов.

10. В треугольнике АВС АВ = 10 см, ВС = 5 см. Найти отношение синуса угла А к синусу угла С:

а) 1/2;

6) 5;

в) 2.

Вариант II

1. Для треугольника АВС справедливо равенство:

2. Площадь треугольника CDE равна:

3. Если квадрат стороны треугольника больше суммы квадратов двух других его сторон, то эта сторона лежит против:

а) острого угла;

б) прямого угла;

в) тупого угла.

4. В треугольнике MNK известны длина стороны MN и величина угла К. Чтобы найти сторону NK, необходимо знать:

а) величину ∠M;

б) длину стороны МК;

в) значение периметра MNK.

5. Треугольник со сторонами 2, 3 и 4 см:

а) остроугольный;

б) прямоугольный;

в) тупоугольный.

6. В треугольнике MNK MN = 2, ∠K = 60°. Радиус описанной около AMNK окружности равен:

а) 4;

б) 2√3/3;

в) 2.

7. Если в треугольнике MNK ∠M= 76°, ∠N = 64°, то наименьшей стороной треугольника является сторона:

a) MN;

б) NK;

в) МК.

8. В треугольнике АВС:

9. По теореме о площади треугольника:

а) площадь треугольника равна произведению двух его сторон на синус угла между ними;

б) площадь треугольника равна половине произведения двух его сторон на угол между ними;

в) площадь треугольника равна произведению половине произведения двух его сторон на синус угла между ними.

10. В треугольнике АВС АВ = 6 см, ВС = 2 см. Найти отношение синуса угла А к синусу угла В:

а) 1/3;

б) 1/4;

в) 3.

Ответы:

Вариант I

Вариант II

II этап. Мотивация к деятельности

Цель деятельности

Постановка учебной задачи

Решение задач с целью подготовки учащихся к восприятию нового материала

(Ф/И) Решить задачу.

Дан параллелограмм ABCD. Найти: а) векторы, коллинеарные б) векторы, сонаправленные в) векторы, противоположно направленные г) векторы, равные д) если е) cos ∠ABC, если

III этап. Учебно-познавательная деятельность

Цель деятельности

Совместная деятельность

Ввести понятие угла между векторами и понятие скалярного произведения векторов

(Ф)

1. Введение понятия угла между векторами (с. 259, рис. 300).

2. Угол а между векторами и не зависит от выбора точки О, от которой откладываются векторы .

3. Угол между сонаправленными векторами считается равным нулю.

4. Обозначение угла между векторами:

5. Определение углов между векторами на рис. 301.

6. Определение перпендикулярных векторов.

7. Повторение сложения и вычитания векторов, умножения вектора на число.

8. Введение понятия еще одного действия над векторами - скалярного умножения векторов. В отличие от суммы и разности векторов скалярное произведение есть число (скаляр) - именно это и обусловило название операции

9. В тетрадях учащиеся оформляют