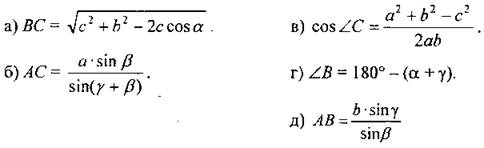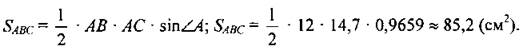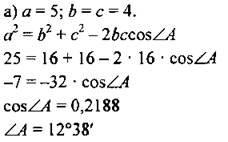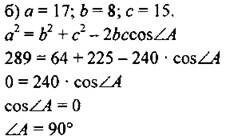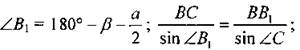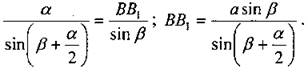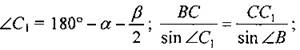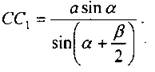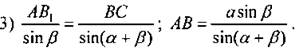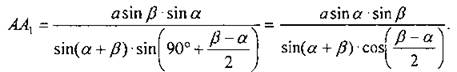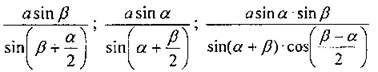РЕШЕНИЕ ТРЕУГОЛЬНИКОВ - СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Цель деятельности учителя

Создать условия для ознакомления учащихся с методами решения треугольников, закрепления знания теорем синусов и косинусов, обучения применению теорем в ходе решения задач

Термины и понятия

Синус, косинус, треугольник, площадь треугольника, прилежащий угол, противолежащий угол

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют применять теоремы синусов и косинусов для решения треугольников

Познавательные: умеют понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации, видеть математическую задачу в контексте проблемной ситуации.

Регулятивные: понимают и сохраняют учебную задачу.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем, участвуют в диалоге.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И): групповая (Г)

Образовательные

ресурсы

• Чертежи для задач

I этап. Актуализация опорных знаний

Цель деятельности

Совместная деятельность

Проверить уровень

теоретических

знаний

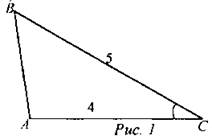
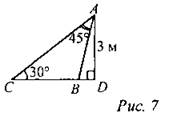
(И)

1. Теоретический опрос: 1-й вариант доказывает теорему синусов; 2-й вариант - теорему косинусов.

2. Устное решение задач по готовым чертежам:

1) Найти АВ.

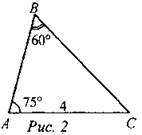
2) Найти АВ.

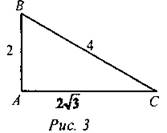
3) Найти угол В.

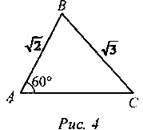
4) Найти угол В.

Ответы:

II этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Создать условия для организации самостоятельного изучения темы урока

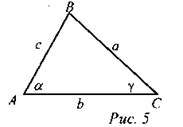
(И) 1. Прочитать самостоятельно в учебнике п. 103 на с. 258-259.

(Ф) 2. Обсудить прочитанный материал, задавая вопросы:

- Что значит “решить треугольник”?

- Перечислите три основные задачи на решение треугольников.

- Составьте план решения треугольников:

1) по двум сторонам и углу между ними;

2) по стороне и двум прилежащим к ней углам;

3) по трем сторонам.

3. Решить треугольник, если (рис. 5):

а) ВС, если АВ = с, АС = b, ∠A = α.

б) АС, если ВС = a, ∠B = β, ∠C = γ.

в) ∠C, если АВ = с, АС = b, ВС = а.

г) ∠В, если ∠А = α, ∠C = γ.

д) АВ, если ∠C = у, ∠B = β, АС = b.

Ответы:

III этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Научить применять теоремы синусов и косинусов при решении задач

(И)

1. По рис. 294 учащиеся самостоятельно разбирают решение примера в учебнике на с. 255.

(Ф/И)

2. Решить № 1026 на доске и в тетрадях.

(Г)

3. Решить № 1029 и 1031 по группам

№ 1026.

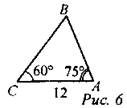
Дано: ∆АВС, АС = 12 см, ∠A = 75°.

Найти: АВ, S_ABC.

Решение:

1) ∠B = 180° - (60° + 75°) = 45°.

2) По теореме синусов:

3)

Ответ: 14,7 см; 85 см².

№ 1031.

Так как против большей стороны лежит острый угол, то ∆АВС - остроугольный.

∆ABC - прямоугольный.

81 = 35 + 36 - 60 ∙ cosα

10 = -60 ∙ cosα

cosα = -0,16666 < 0, следовательно ∠α - тупой.

∆ABC - тупоугольный.

№ 1029.

Дано: ∆АВС, ВС = а, ∠B = α, ∠C = β

Найти: биссектрисы.

Решение:

1) Рассмотрим ∆ВСВ₁:

2) Рассмотрим ∆ВСС₁:

4) Рассмотрим ∆АВА₁:

Ответ:

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что значит “решить треугольник”?

- Задайте три вопроса по уроку

(И) Домашнее задание: решить № 1027, 1028, 1032