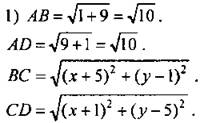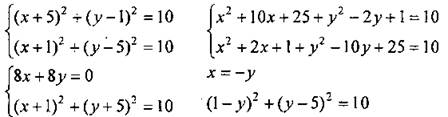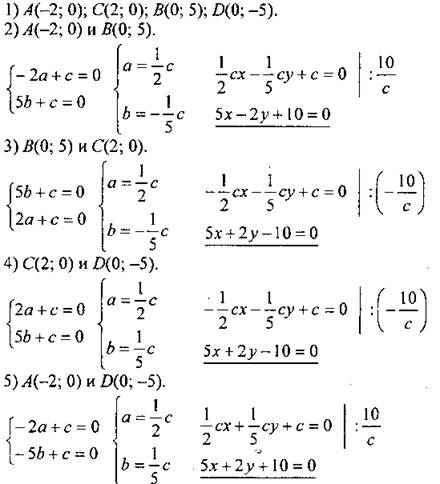Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
РЕШЕНИЕ ЗАДАЧ - Урок 2 - МЕТОД КООРДИНАТ
|
Цель деятельности учителя |
Создать условия для совершенствования навыков решения задач, подготовки к контрольной работе |
||
|
Термины и понятия |
Прямая, уравнение прямой, окружность, уравнение окружности, метод координат |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Владеют базовым понятийным аппаратом, навыками устных, письменных, инструментальных вычислений; умеют применять метод координат |
Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: понимают и сохраняют учебную задачу; умеют контролировать процесс и результат учебной деятельности. Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками. Личностные: проявляют познавательный интерес к изучению предмета |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные ресурсы |
• Задания для самостоятельной работы |
||
|
I этап. Актуализация знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить уровень сформированности теоретических и практических знаний и навыков |
(Ф/И) 1. Обсуждение вопросов учащихся по домашнему заданию, сообщение результатов математического диктанта. 2. Опрос по теории: - Сформулируйте теорему о разложении вектора по двум данным неколлинеарным векторам. - Запишите формулы координат середины отрезка по координатам его концов. - Напишите уравнение окружности с центром в точке В(4; 0), если она проходит через точку А(7; 4). - Сформулируйте правило нахождения координат разности двух векторов. - Напишите формулу для вычисления длины вектора по его координатам. - Сформулируйте правило нахождения координат произведения вектора на число по заданным координатам вектора |
||
|
II этап. Самостоятельная работа |
|||
|
Цель деятельности |
Задания для самостоятельной работы |
||
|
Выявить уровень развития умения применять теоретические знания |
(И) Вариант I 1. Окружность с центром в точке А(-5; 3) проходит через точку В(2; -1). Напишите уравнение этой окружности. 2. Напишите уравнение прямой, проходящей через начало координат и точку В(-2; 4). 3. Выясните взаимное расположение прямой х = -5 и окружности (х - 7)2 + (у - 6)2 = 81. Вариант II 1. Окружность с центром в точке М(2; -4) проходит через точку N(-3; 1). Напишите уравнение этой окружности. 2. Напишите уравнение прямой, проходящей через начало координат и точку С(-6; -3). 3. Выясните взаимное расположение прямой у = 25 и окружности (х - 5)2 + (у - 7)2 =100. Ответы: Вариант I 1. (х + 5)2 + (у - 3)2 = 65. 2. 2х + у = 0. 3. Нет общих точек Вариант II 1. (х - 2)2 + (у + 4)2 = 50. 2. х - 2у = 0. 3. Нет общих точек. |
||
|
III этап. Решение задач |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Совершенствовать навыки решения задач |
(Ф/И) 1. Решить на доске и в тетрадях № 997. 2. Решить на доске и в тетрадях № 999. 3. Решить на доске и в тетрадях № 980. 4. Решить на доске и в тетрадях № 1004. 5. Решить на доске и в тетрадях № 1007 |
№ 997.
Дано: А(3; 2); 5(0; 5); С(-3; 2); В(0; -1). Доказать: ABCD - квадрат. Доказательство:
№ 999. Дано: ABCD - параллелограмм. А(-4; 4); В(-5; -1); С(х; у); D(-1; 5). Найти: (х; y). Решение:
Так как в параллелограмме стороны попарно равны, то:
1 - 2у + у2 + у - 10у + 25 - 10 = 0 у2 - 6у + 8 = 0 2y2– 12y + 16 = 0 y1 = 4 у2 = 2 Если у = 4, то х = -4 - известна А(-4; 4). Если у = 2, то х = -2 - известна С(-2; 2). № 980.
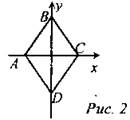
Дано: ABCD - ромб. АС є Ox, BD є Оу; АС = 4 см, BD = 10 см. Написать уравнение АВ, ВС, CD, AD. Решение
№ 1004. Дано: а1х + b1у – с1 = 0 l1: 3х - 1,5у + 1 = 0 а2х + b2у – с2 = 0 l2: 2х – у - 3 = 0 Доказать: l1 ll l2. Доказательство: Условие l1 ll l2 выполнено, если а1 ∙ b1 - a2 ∙ b2 = 0, то есть 3 ∙ (-1) - 2 ∙ (-1,5) = 0 - 3 + 3 = 0. 0 = 0 - верно, следовательно, l1 ll l2, что и требовалось доказать. № 1007.
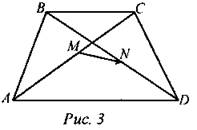
Дано: ABCD - трапеция. М є АС, АМ = МС, N є BD, BN = ND. Доказать: Доказательство:
|
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Сформулируйте три вопроса по данной теме. - Оцените свою работу на уроке |
(И) Домашнее задание: подготовиться к контрольной работе; решить № 990, 1010 |
||
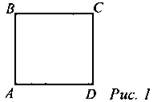
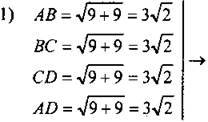 ABCD - ромб (по признаку)
ABCD - ромб (по признаку)