КОНТРОЛЬНЫЕ РАБОТЫ - Урок 2 - ГЕОМЕТРИЯ - ОТВЕТЫ

(по учебнику Л.С. Атанасяна и др.)

К1

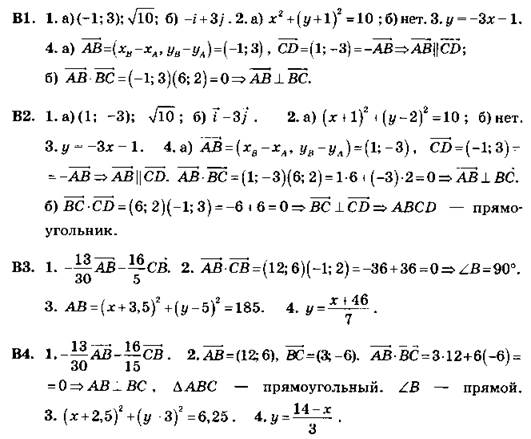
К2

Для доказательства того, что треугольник прямоугольный, достаточно показать, что

3. 2. Для доказательства того, что Δ — прямоугольный, достаточно показать, что

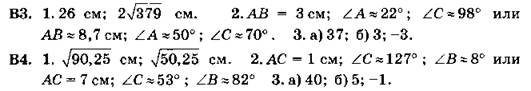
К3

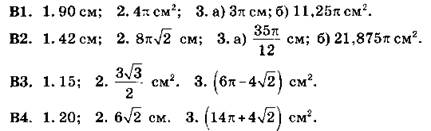
К4

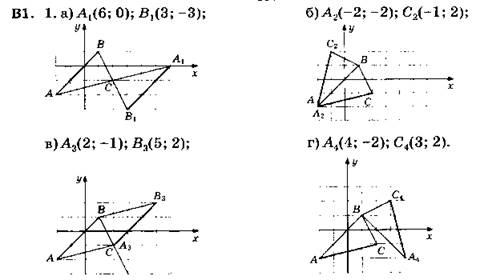
2. Соответствующие стороны квадратов параллельны.

3. А → С, В → А, С → В.

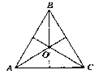
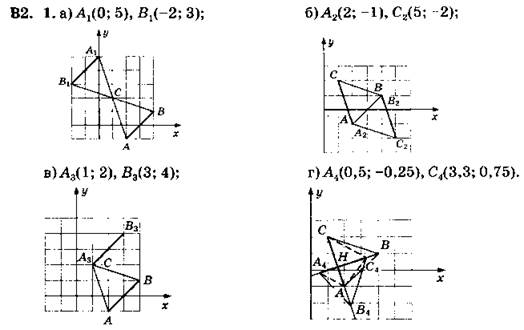
Пунктиры даны, чтобы выделить равнобедренные прямоугольные треугольники. Координаты приблизительны.

2. Соответствующие стороны параллельны.

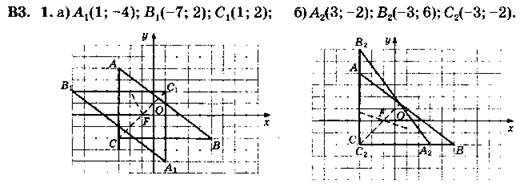
Пунктиром изображены биссектрисы углов треугольников.

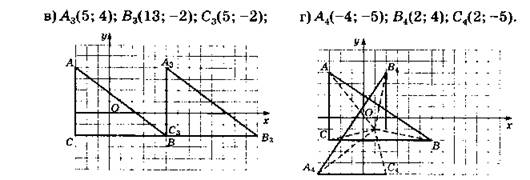
Пунктиры проведены, чтобы обозначить прямые углы.

2. Можно. Второе уравнение приводится к виду (х - 4)² + (у - 5)² = 20, т.е. тот же радиус √20.

3. Пусть АВ = CD. Если АВ и CD не параллельны, то искомая точка — пересечение серединных перпендикуляров АС и BD.

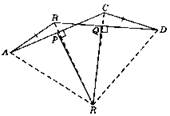
AR = CR, BR = DR, ΔABR = ΔCDR. При повороте вокруг точки R на угол ACR AACR перейдет в A BDR. Поэтому А → С, В → D.

Если же AB ││ CD, то получается параллелограмм и при повороте на 180° относительно пересечения диагоналей получаем А → С, B → D или A → D, В → С (смотри рис.).

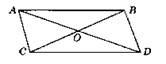
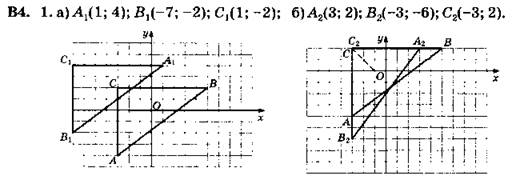
Пунктиром изображена биссектриса прямого угла треугольника АВС.

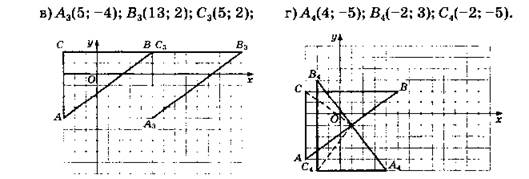
Пунктиры проведены, чтобы обозначить прямые утлы.

2. Выделением полного квадрата второе уравнение приводится к виду (х + 4)² + (х - 5)² =20. Радиусы обеих окружностей равны √20. Поэтому можно. Ответ: Да.

3. По условию А → В , С → D . Центр угла поворота должен быть на серединном перпендикуляре к АВ и к CD, поэтому на их пересечении. Но они параллельны. Поэтому они совпадают. Значит, АО = ОВ, СО = OD. Если в качестве центра угла поворота взять точку О, то угол поворота равен 180°.

Если в качестве центра угла поворота взять точку F, то углы поворота для точек А и С — разные, а должны быть одинаковыми. Значит, центр угла поворота — точка О, а угол поворота — 180°. Ответ: 180°.

К5