Контрольные и самостоятельные работы по алгебре и геометрии 9 класс - 2016 год
Теорема синусов и ее следствия - РЕШЕНИЕ ТРЕУГОЛЬНИКОВ - САМОСТОЯТЕЛЬНЫЕ РАБОТЫ - ГЕОМЕТРИЯ
Вариант 1
1. По данным рисунка найдите х.
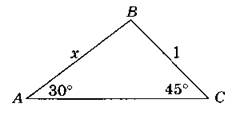
2. В треугольнике ABC ∠B = 55°, ∠C = 25°. Укажите наибольшую сторону треугольника. Ответ объясните.
3. В треугольнике ABC ∠B = 60°, AС = 4√3 см. Найдите диаметр окружности, описанной около этого треугольника.
Вариант 2
1. По данным рисунка найдите угол х.
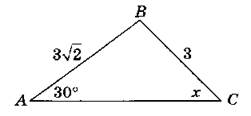
2. В треугольнике ABC ∠A = 35°, ∠C = 75°. Укажите наименьшую сторону треугольника. Ответ объясните.
3. Один из углов треугольника ∠B = 30°, АС = 10 см. Найдите диаметр окружности, описанной около треугольника.
Вариант 3
1. Дано: AD — биссектриса треугольника АВС; BD = а, ∠B = β; ∠BAD = а. Найти DC.
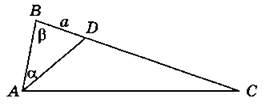
2. В параллелограмме ABCD точка М — середина стороны ВС. Известно, что ∠B — тупой. Сравните углы AMB и DMC.
3. Две стороны треугольника равны 6 см и 8 см, а третья сторона равна радиусу окружности, описанной около треугольника. Найдите третью сторону.
Вариант 4
1. Дано: АС = b; ∠A = a; ∠CDB = β; ∠B = γ. Найти BD.
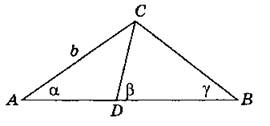
2. В параллелограмме ABCD точка М — середина стороны ВС. Известно, что ∠MDA > ∠MAD. Определите, какие из углов параллелограмма острые.
3. Две стороны треугольника равны 4 см и 3 см. Определите, какую длину может иметь третья сторона с, если она связана с радиусом соотношением с = R√3.