Квадратичная функция - КОНТРОЛЬНЫЕ РАБОТЫ - АЛГЕБРА

Вариант 1

1. Разложите на множители квадратные трехчлены:

а) х² + 4х- 21;

б) 6у² + 13у - 5.

2. Постройте график функции у = х² - х - 6.

а) Найдите по графику функции промежутки, в которых у > 0 и у < 0.

б) Не выполняя дополнительных построений, найдите координаты точек пересечения данного графика с графиком функции у = 2х + 12.

3. Сократите дробь:

4. Определите значение x, при котором функция у = 2х² - 8х + 7 принимает наименьшее значение. Найдите это значение.

Вариант 2

1. Разложите на множители квадратные трехчлены:

а) 2х² - 15х - 77;

б) у² - 3у - 40.

2. Постройте график функции у = х² + х - 6.

а) Найдите по графику функции промежутки, в которых у > 0 и у < 0.

б) Не выполняя дополнительных построений, найдите координаты точек пересечения данного графика с графиком функции у = 2х - 4.

3. Сократите дробь:

4. Определите значение х, при котором функция у = 3х² + 6х - 5 принимает наименьшее значение. Найдите это значение.

Вариант 3

1. Сократите дробь:

2. Постройте график функции у = х² – 6|х| + 6. Пользуясь графиком, найдите промежутки монотонного возрастания и убывания данной функции.

3. Задайте аналитически уравнение прямой, проходящей через точки пересечения графиков функций у = 3х - х² и у = х² - 5х.

4. Выполните действия:

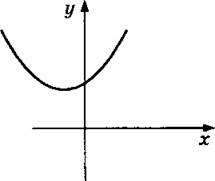
5. Пользуясь графиком функции у = ах² + bх + с, изображенным на рисунке, определите знаки чисел а, b, с и дискриминанта квадратного трехчлена ах² + bх + с.

Вариант 4

1. Сократите дробь:

2. Постройте график функции у = |x² – 5x + 6|. Пользуясь графиком, найдите промежутки монотонного возрастания и убывания данной функции.

3. Задайте аналитически уравнение прямой, проходящей через точки пересечения графиков функций у = x² – 6x и у = 4х + 3x².

4. Выполните действия:

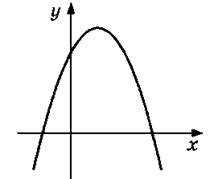
5. Пользуясь графиком функции у = ах² + bх + с, изображенным на рисунке, определите знаки чисел а, b, с и дискриминанта квадратного трехчлена ах² + bх + с.