Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА - ПЛОЩАДЬ
|
Цель деятельности учителя |
Создать условия для выведения формулы площади параллелограмма |
||
|
Термины и понятия |
Равновеликие многоугольники, равносоставленные многоугольники, площадь квадрата, площадь прямоугольника, площадь параллелограмма |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Владеют базовым понятийным аппаратом; умеют работать с геометрическим текстом |
Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение. Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи. Коммуникативные: умеют находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И); групповая (Г) |
||
|
Образовательные ресурсы______ |
• Учебник. • Задания для индивидуальной, фронтальной работы |
||
|
I этап. Актуализация опорных знаний |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить правильность выполнения домашнего задания, подготовить учащихся к восприятию новой темы |
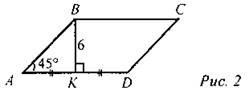
(И) К доске вызываются три ученика для оформления решения домашних задач. В это время учитель проводит теоретический опрос, 3-6 учащихся работают по индивидуальным карточкам. После теоретического опроса проверяют правильность решения домашнего задания. Теоретический опрос. - Перечислите основные свойства площадей. - Сформулируйте и докажите теорему о площади прямоугольника. Работа по карточке. 1. Периметр квадрата равен 20 см. Прямоугольник имеет такую же площадь, что и квадрат, а одна из его сторон равна 10 см. Найдите периметр прямоугольника. 2. Найдите площадь прямоугольника с периметром 60 см и отношением сторон 1:2. Решение задач: (Ф) 1. Дано: ABCD - параллелограмм, ВМ = 4, MN = 6, ВМ ⊥ AD, CN ⊥ AD. Доказать: SABM = SDCN. Найти: SABCD.
2. Дано: ABCD - параллелограмм. Найти: SABCD.
|
||
|
II этап. Изучение нового материала |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Доказать формулу для вычисления площади параллелограмма |
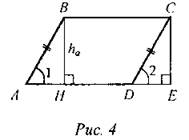
(Ф) 1. Ввести понятие высоты параллелограмма. На доске и в тетрадях - рисунок.
ВН - высота, проведенная к стороне AD параллелограмма ABCD. ВК - высота, проведенная к стороне CD параллелограмма ABCD. (Г/Ф) 2. Задача. Дано: ABCD - параллелограмм, AD = а, ВН - высота, ВН = h. Найти: SABCD. (Разбить учащихся на группы по 3-4 человека, дать на обдумывание 3-5 минут, а затем обсудить решение задачи, выслушав все варианты и выбрав среди предложенных наиболее удачный. Решение задачи оформляется в виде теоремы на доске и в тетрадях. У доски работает один из наиболее подготовленных учащихся.) Теорема: S = а ∙ ha, где а - сторона параллелограмма, ha - высота, проведенная к ней.
Доказательство: 1) Проведем ВН ⊥ AD, СЕ ⊥ AD. 2) ∆АВН = ∆DCE по гипотенузе и острому углу (АВ = СD как противолежащие стороны параллелограмма; ∠1 = ∠2, так как ∠2 = 180° - ∠ADC и ∠1 + ∠2 = 180°, как сумма внутренних односторонних углов при параллельных прямых АВ и CD и секущей AD; ∠AHB = ∠CED = 90°) => SABH = SDCE, DE = АН. 3) SABCD = SABH + SHBCD = SDCE + SHBCD = SHDCE. HBCE - прямоугольник, SHBCE = HE ∙ BH; HE = HD + DE, но так как DE = АН, то НЕ = АН + HD = AD, то есть SHDCE= AD ∙ ВН = a - ha, отсюда SABCD = a - ha |
||
|
III этап. Закрепление изученного материала |
|
|
Цель деятельности |
Совместная деятельность |
|
На простых задачах отработать применение формулы площади параллелограмма |
(Ф) Решить задачи: № 459 (а) (устно), 459 (б, в), 464 (в) (устно) |
|
Самостоятельная работа |
|
|
Задания для самостоятельной работы |
|
|
Вариант I Стороны параллелограмма 10 см и 6 см, а угол между этими сторонами 150°. Найдите площадь этого параллелограмма. 1. ∠В = 180° - 150° = 30°. 2. Катет АЕ лежит против угла 30°, поэтому АЕ = 0,5АВ = 3 см. 3. SABCD = BC ∙ AE = 10 ∙ 3 = 30 (см2).
Вариант II Острый угол параллелограмма равен 30°, а высоты, проведенные из вершины тупого угла, равны 8 см и 3 см. Найти площадь параллелограмма. 1. Катет ВМлежит против угла в 30°, поэтому АВ = 2ВМ = 6 см. 2. SABCD = ВК ∙ DC = 8 ∙ 6 = 48 (см2).
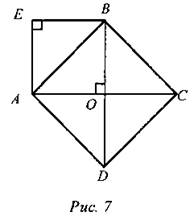
Вариант III Найдите площадь ромб, диагонали которого равны 8 см и 6 см. Использовать задание 3 из домашней работы. ВО = OD = 4 см, АО = ОС = 3 см. SaEBO = 3 ∙ 4 = 12 (см2). SABCD = 12 ∙ 2 = 24 (см2).
Организовать проверку, открыв доску с правильным решением. Подвести учащихся к выводу, что площадь ромба равна половине произведения его диагоналей |
|
|
IV этап. Итоги урока. Рефлексия |
|
|
Деятельность учителя |
Деятельность учащихся |
|
(Ф) - По каким формулам можно вычислить площадь параллелограмма и площадь ромба? - Что нового узнали на уроке? - Оцените свою работу |
(И) Домашнее задание: § 2, вопрос 4, с. 133; № 459 (г), 460, 464 (б). По желанию: 1. Найдите углы параллелограмма, если его площадь равна 20 см2, а высота, проведенная из вершины тупого угла, делит одну из сторон на отрезки 2 см и 8 см, считая от вершины острого угла. Ответ: 45°; 135°. 2. Сравните площади параллелограмма и прямоугольника, если они имеют одинаковые основания и одинаковые периметры. Ответ: площадь прямоугольника больше площади параллелограмма |