ОТВЕТЫ

Обучающие работы

O2

В 1. 1) 110°.2) 20 см и 8 см.

В 2. 1) 45°; 135°. 2) 10 см и 20 см.

В 3. 1) 45°; 135°. 2) 5 см и 6 см.

В 4. 1) 40°; 140°. 2) 56 см.

O3

Указание ко всем задачам. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

В 1. 1) 96°; 84°. 2) 86 см.

В 2. 1) 70°; 110°. 2) 6 см и 12 см.

В 3. 1) 96°; 84°. 2) 5 см и 15 см.

В 4. 1) 68°; 112°. 2) 30 см.

O4

В 1. 1) 20 см и 10 см. 2) 40°; 140°; 40°; 140°.

В 2. 1) 3 см. 2) 60°; 60°; 120°; 120°.

В 3. 1) 8 см. 2) могут, например, 50°; 130°; 110°; 70°.

В 4. 1) 66°; 114°; 66°; 114°.

Указание. Биссектриса угла трапеции отсекает равнобедренный треугольник. Углы при основании равнобедренной трапеции равны. 2) 24 см и 12 см.

O5

В 1. 1) 60°; 30°. 2) 3 см и 6 см.

В 2. 1) 10 см, 10 см.

В 3. 1) 41 см, 41 см.

В 4. 1) 40 см.

O6

В 1. 1) 110°; 70°; 110°. 2) 40.

В 2. 1) равнобедренный, 130°; 25°; 25°. 2) квадрат.

В 3. 1) 70°; 20°; 90°. 2) прямоугольный, равнобедренный, 45°; 45°; 90°.

В 4. 1) прямоугольный, равнобедренный, 45°; 45°; 90°. 2) ромб.

O7

В 1. 1) 12 см. 2) 117 см².

В 2. 1) √10 см. 2) 160 см².

В 3. 1) 6√6 см. 2) 36 см.

В 4. 1) √30 см. 2) 80 см.

O8

В 1. 1) 7,5 см². 2) 24 см². 3)10 см.

Б 2. 1) 6 см. 2) 48 см. 3) 70 см².

В 3. 1) б см и 8 см. 2) 8 см. 3) 260 см².

Б 4. 1) 6 см. 2) 10 см и 24 см. 3) 120 см².

O9

В 1. 1) √97 см. 2) АВ = 25 м, АС = 15 м, ВС = 20 м.

В 2. 1) 4√17 см. 2) АВ = 11 дм, АС = √89 дм, ВС = 10 дм.

В 3. 1) 12 м. 2) 21 см.

В 4. 1) 15 м. 2) 25 м.

О10

Б 1. 1) 5 см. 2) 13 и 14. АС = 21 см или 9 см, ВС = 10 см.

Б 2. 1) 8 см. 2) 17 и 21.

Б 3. 1) 4, 10, 24, 6√5. 2) АВ = 17 см,

В 4. 1) 7, 18, 10, √89. 2) 25 см или 7 см.

О11

В 1. 1) 13 м. 2) 16.

Б 2. 1) 15 м. 2) 12.

Б 3. 1) 24 см. 2) 8, 4√5.

Б 4. 1) 24 см. 2) 8, 8√5.

О12

В 1. 1) 240 см². 2) 60 см².

В 2. 1) 24 см². 2) 300 см².

В 3. 1) 384 см². 2) 15,6 см².

Указание. Дополнительное построение. Через вершину тупого угла провести прямую, параллельную одной из боковых сторон. Она разделит трапецию на параллелограмм и прямоугольный треугольник (по теореме, обратной теореме Пифагора).

В 4. 1) 88. 2) 9.

Указание. Медиана треугольника разбивает его на два равновеликих треугольника.

О14

В 1. 1) 21 см; 30 см; 24 см. 2) подобны.

В 2. 1) 70 см. 2) подобны.

В 3. 1) 4,5 см, 3,6 см. 2) 12.

В 4. 1) 5,4 см, 4,5 см. 2) 7,5.

О15

Б 1. 25 см, 15 см, 20 см, 150 см².

В 2. 25 см, 15 см, 150 см².

В 3. 25 см, 20 см, 150 см².

В 4. 25 см, 15 см, 20 см, 150 см².

О16

В 1. 1) 6,5 см; 6 см; 7,5 см. 2) ромб; 24 см. В 3. 1) 14,5. 2) ромб, 30 см.

В 2. 1) 20 см, 30 см, 26 см. 2) ромб; 118 см. В 4. 1) 24, 18, 16. 2) 18.

О17

В 1. 1) 6 см. 2) 12√2. 3) 45°; 45°.

В 3. 1) 8 см. 2) 12√3. 3) 60°; 30°.

В 2. 1) 12 см. 2) 24. 3) 60°; 30°.

В 4. 1) 7 см. 2) 12√3. 3) 60°; 30°.

O18

В 1. 1) ≈ 29 см; “17 см. 2) ≈ 53°; ≈ 127°. 3) 20 см; ≈ 39 см; ≈ 39 см.

В 2. 1) ≈ 7,5 см; ≈ 5,8 см. 2) ≈ 73°; ≈ 107°. 3) 7,5 см; ≈ 14,5 см.

В 3. 1) ≈ 8,8 см; 12,7 см. 2) ≈ 10°; ≈ 170°. 3) ≈ 6,2 см; 6,5 см.

В 4. 1) ≈ 4,8 см; ≈ 9 см. 2) ≈ 82°; ≈ 98°. 3) 15 дм; 18 дм.

О19

В 1. 1) 24° или 156°. 2) 69°

В 2. 1) 54° или 126°. 2) 76°

В 3. 1) 68°. 2) 58°

В 4. 1) 84°. 2) 43°

O20

В 1. 1) 10 см и 2 см. 2) 45°; 45°; 90°. 3) 15, 20, 12.

В 2. 1) 6; 8. 2) 45°; 45°; 90°. 3) 6 и 24.

В 3. 1) 3. 2) 25°; 40°; 115°. 3) 8 и 12.

В 4. 1) 3 и 10. 2) 34°; 36°; 110°. 3) 9 см и 16 см; AM = AN = 15 см; МВ = BN = 20 см.

O21

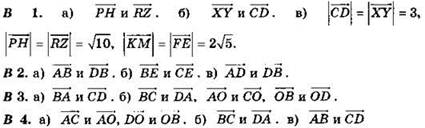Равных векторов нет.

O23

В 1. 2) X > 0.

В 2. 2) х = 1.

В 3. 2) x = -1

В 4. 2) x < 0

Математические диктанты

М1

1) а) 6 см. б) 6 см. в) 15 см

2) а) 18 см. б) 11 см. в) 100° и 80°

М2

1) 18 см. 2) 43°. 3) 5 см, 3 см, 3 см. 4) 60°, 120°. 5) 6,4 см

М3

1) Да. 2) Нет. 3) Да. 4) Да. 5) Нет. 6) Нет. 7) Квадрат

М4

1) Прямоугольная трапеция

2) Прямоугольник

3) Равнобедренный прямоугольный треугольник

5) 8

М5

1) б) 24 см². 2) в) 17,5 см². 3) в) 80 см². 4) в) 14 см². 5) 4 см²

М6

2) 15 см. 3) 6 см. 4) 52 см. 5) 50 см²

М7

3) а) Пересекается, б) Касается, в) Не имеет общих точек. 4) 5 см. 5) д) 3√3 см.

Проверочные работы

П1

В 1. 1) 8,5 см. 2) 136°, 44°, 136°. 3) параллелограмм, 130°, 50°, 130°, 50°.

В 2. 1) 9,5 см. 2) 36°, 144°, 36°. 3) параллелограмм, 120°, 60°, 120°, 60°.

В 3. 1) 2 см и 6 см. 2) 70°, 20°, 90°.

В 4. 1) 3 см и 12 см. 2) 50°, 40°, 90°.

П2

В 1. 2) 45°, 45°, 90°. 4) ромб, 52 см.

В 2. 2) 90°, 22°.

В 3. 2) 16 см и 16 см. 4) ромб, 64 см.

В 4. 1) 45°, 45°, 90°.

П3

В 1. 1) 10 см. 2) 204 м². 3) √5 см и 2√5 см. 4) 16 см и 8√5 см.

В 2. 1) 13 см. 2) 48 см². 3) 2√10 см и 6√10 см. 4) 5√2 см и 7 см.

В 3. 1) 12 см. 2) 104 м². 3) 2√3 м. 4) 6√5 см и 12 см.

В 4. 1) 10√7 см. 2) 48 см². 3) 2√2 м. 4) 7 см и 5√2 см.

П4

Б 1. 1) 12 sinβ, 12 cosβ. 2) 25. 4) 25

Б 2. 1) 16 sinγ, 16 cosγ. 2) 15 см. 4) 24 см.

Б 3. 1) 16 sinα, 16 cosα. 2) 20 см. 4) 36.

В 4. 1) 18 sinβ, 18 cosβ. 2) 24 см. 4) 9

П5

Б 1. 1) 65°; 25°; 90°. 2) 10 см. 3) 9 см и 8 см. 4) 3 см, 7 см.

Б 3. 1) 28°; 62°; 90°. 2) 12 см. 3) 4 м, 18 м. 4) 12 см и 8 см.

Б 2. 1) 65°. 2) 12 см. 3) 4 см и 15 см. 4) 8 см и 10 см.

В 4. 1) 30°. 2) 12 см и 5 см. 3) 5 см. 4) 13 см и 7 см.

Контрольные работы

К1

Задачи для подготовки к контрольной работе

1. 1, 2, 4, 5, 8, 9, 10, 12

2. 35°, 55°, 90°.

3. 6 см и 8 см.

4. Указание. Используйте свойство диагоналей прямоугольника.

5. ромб, 36 см.

6. Указание. Используйте признак равнобедренного треугольника и свойства углов при параллельных прямых и секущей.

7. см. рисунки.

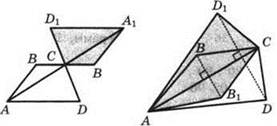
B 1.

1. 1, 3, 5.

2. 27.

3. 4 см.

4. 70°, 20°, 90°.

5. см. рисунок.

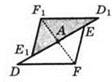
6. 56.

В 2.

1. 1, 2, 4.

2. 25.

3. 3 см.

4. 50°, 40°, 90°.

5. см. рисунок.

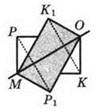
6. 58.

В 3.

1. 1, 3, 4.

2. 45.

3. 3 см.

4. 60°, 30°, 90°.

5. см. рисунок.

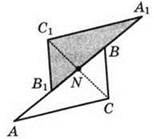
6. 54.

В 4.

1. 1, 2, 5.

2. 18.

3. 7 см.

4. 80°, 10°, 90°.

5. см. рисунок.

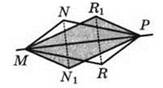
6. 52.

К2

Задачи для подготовки к контрольной работе

1. а) 21. б) 126. в) 84. г) 138.

2. 50 м.

3. 120.

4. 4√10 см, 12 см.

5. 2√3 м.

6. 19,2.

7. 9 см, 3√10 см.

В 1. 1. 1. 2. 13 см. 3. 24 см. 4. 88 см². 5. 6.

В 2. 1. 3. 2. 15 см. 3. 10 см. 4. 144 см². 5. 20/3.

В 3. 1. 4. 2. 20 см. 3. 16 см. 4. 132 см². 5. 4.

В 4. 1. 3. 2. 9 см. 3. 13 см. 4. 104 см². 5. 2,4.

К3

Задачи для подготовки к контрольной работе

1. 9√3.

2. 12 cos α + 5.

3. 18.

4. 15.

5. 7,2.

6. 4/3.

7. трапеция, 36.

8. 4, 5.

9. 5 и 4.

В 1. 1. 2. 2. 4. 3. 16. 4. 10/√3. 6. 3/4.

В 3. 1. 3. 2. 1. 3. 15. 4. 16√3. 6. 2/3.

В 2. 1. 1. 2. 3. 3. 9,6. 4. 20√3. 6. 0,8.

В 4. 1. 1. 2. 2. 3. 20. 4. 12√3. 6. 0,8.

К 4

Задачи для подготовки к контрольной работе

1. 24 см.

2. 2, 4, 6.

3. 1) 75°. 2) а) 30°. б) 170°. 3) 70°.

4. 18 м, 4 м.

5. 12 см.

6. 48 см.

7. 30°.

В 1. 1. 4. 2. 2. 3. 10 см. 4. 6. 5. 6√3 см. 6. 3 см.

В 3. 1. 1. 2. 4. 3. 12 см. 4. 16 см. 5. 55 см. 6. 8 см.

В 2. 1. 3. 2. 1. 3. 12 см. 4. 12 см. 5. 35 см. 6. 10 м.

В 4. 1. 2. 2. 2. 3. 5 см. 4. 15. 5. 4 см. 6. 7 м.

К 5

Задачи для подготовки к контрольной работе

1. а) 1, 4, 6. б) 1, 2, 3, 4, 6, 8. в) 1, 4, 5, 6, 7.

2. а) 40. б) 112. в) 152.

4. m² sin α.

5. 8 см и 16 см.

6. 4 см.

7. 24 см.

В 1. 1. 2, 3. 2. 2. 3. 1. 4. 5 см. 5. 84 см². 6. 9 см. 7. 20/3 см и 16/3 см.

В 2. 1. 1, 3. 2. 3. 3. 3. 4. 15 см. 5. 117 см². 6. 14 см. 7. 80/7 см и 60/7 см.

В 3. 1. 2, 4. 2. 3. 3. 4. 4. 9 см. 5. 96 см². 6. 9 см. 7. 9/2 см и 15/2 см.

В 4. 1. 1, 4. 2. 4. 3. 4. 4. 20 см. 5. 91 см². 6. 10 см. 7. 60/7 см и 45/7 см.

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ

Дополнительные задачи. Тема № 1. Четырехугольники

1. 12,5 см.

2. 46°, 31°, 103°.

3. 1) 4 см, 16 см; 2) 6,5 см, 13,5 см.

6. 23 см.

7. 16 см.

9. 40°, 40°, 100° или 50°; 50°; 80°.

10. 80°, 10°, 90°.

11. 60°, 120°, 60°, 120°.

12. 11.

15. 41°, 34°, 105°.

16. 2) 42 см.

17. 51°, 39°.

18. Указание. Биссектриса угла трапеции отсекает равнобедренный треугольник, треугольник МРК — равнобедренный с основанием МК, 140°.

19. Указание. Биссектриса угла трапеции отсекает равнобедренный треугольник, 29 см.

20. 16 м.

21. Неверно.

22. Неверно.

23. Верно.

24. Верно.

25. Верно.

26. Верно.

27. Неверно.

28. Неверно.

29. Верно.

30. Неверно.

31. Верно.

32. Неверно.

33. Верно.

34. Верно.

35. Неверно.

36. Верно.

37. Верно.

38. Верно.

39. Неверно.

40. Верно.

41. Верно.

42. 56 см или 58 см.

Указание. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

Дополнительные задачи. Тема № 2. Площадь. Теорема Пифагора

1. 10 см.

2. 10 см.

3. Указание. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине, 12 см.

4. 8 см.

5. 32 см.

6. 4 см.

7. 80 см.

8. 27 см.

9. 2 см и 2√3 см. Указание. Проведите прямую через вершину тупого угла трапеции параллельно боковой стороне. Трапеция разделится на параллелограмм и прямоугольный треугольник.

10. 2,5 см. Указание. Проведите через середину меньшего основания прямые, параллельные боковым сторонам. Они отсекут в трапеции треугольник со сторонами 3 см, 4 см, 5 см. Треугольник прямоугольный (по теореме, обратной теореме Пифагора). Искомый отрезок является медианой этого треугольника и равен половине гипотенузы.

11. 150 см².

12. 12√2 см.

13. 4√3 см.

14. 30 см².

15. 2√2 см.

16. 1) 15 см; 2) 6 см; 3) 21 см или 9 см

17. 48 см².

18. 240 см².

19. 30√3 см².

20. 198 см².

21. 88.

22. 32,5 см².

23. 36√3 см².

24. 32 см.

25. Указание. Медиана треугольника делит его на два равновеликих треугольника. Три медианы треугольника делят его на шесть частей, равных по площади. 6 см², 1,5 см².

26. Верно.

27. АВ = 20/9.

Решение. Пусть АВС — данный треугольник, АС = 5, ВС = 4, AD, ВE, СР — высоты треугольника, S — площадь треугольника.

2S = 5BE = 4AD = АВ ∙ СР.

Тогда BE = 0,4S, AD = 0,5S, следовательно, CP = 0,9S.

AB = 2S : CP = 20/9.

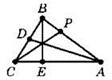
28. 2√5.

Указание. Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины.

Решение.

1) Треугольник АВС, ВС = 8, АС = 6, ВК и AM — медианы, пересекаются в точке О.

2) Пусть ОМ = х, ОК = у, тогда ОА = 2х, ОВ = 2у.

3) Применим к прямоугольным треугольникам ВОМ и КОА теорему Пифагора, получим х² + у² = 5.

4) Для прямоугольного треугольника АОВ АВ² = (2x)² + (2у)² = 20.

5) АВ = 2√5.

29. 0,96 м².

30. 7 м, 13 м.

32. 96 см².

Указание. Диагональ данной трапеции отсекает равнобедренный треугольник.

33. 60 см.

34. 6,25 см.

Решение.

1) Пусть треугольник АВС равнобедренный с основанием АС, ВН и AM - высоты. ВН = 5 см, AM = 6 см.

2) S_ABC = 0,5 АС ∙ ВН = 0,5 ВС ∙ AM

5 АС = 6 ВС, т.е. ВС : АС = 5 : 6, ВС : СН = 5 : 3, ВС = 5x, СН = 3x.

3) В треугольнике ВНС по теореме Пифагора 25 + 9x² = 25x² х = 1,25, ВС = 5 ∙ 1, 25 = 6, 25 (см).

35. 144√3 см².

Дополнительные задачи. Тема № 3. Подобие треугольников. Решение прямоугольных треугольников

1. 2) 21; 3) ОР = 15, НК = 15.

2. 3) 20 см, 28 см.

6. 1) параллелограмм; 2) 2а; 3) 10,5 см.

7. 2р.

8. 1) 16√3 см; 2) ≈ 18 см; 3) ≈ 8 см.

9. АВ = 3√2 см, АС = 2√3 см, BС = 3 + √3 см.

10. ≈ 11.

11. h²√3.

12. MK = 3.

Решение.

Треугольники МВК и АВС подобны.

Пусть AM = ВК = х, тогда

13. 24.

Указание. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

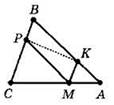
Решение.

1) Треугольники СРМ и МКА подобны (по двум углам), коэффициент подобия равен 2.

2) Пусть МА = х, МК = у, АК = z.

Тогда РВ = у, СР = 2у, СМ = 2х, РМ = ВК = 2z.

3) Получаем следовательно, треугольники СBА и МКА подобны (по трем сторонам), коэффициент подобия равен 3.

14. 49.

Указание. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Отношение площадей треугольников с общей высотой равно отношению соответствующих сторон.

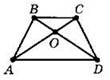
Решение

1) Треугольники AOD и СОВ подобны (по двум углам), коэффициент подобия равен 4/3.

15. В 4 раза.

16. 2,5.

Указание. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Отношение площадей треугольников с общей высотой равно отношению соответствующих сторон.

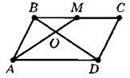
Решение.

1) Диагональ BD делит параллелограмм на две равные части. S_ABD = S_CBD = 3.

2) Треугольники BOM и DOA подобны (по двум углам), коэффициент подобия равен 0,5.

20. Верно.

21. 24 или 6.

22. Ромб, 52 см.

23. Прямоугольник. Указание. Четырехугольник, вершинами которого являются середины сторон выпуклого четырехугольника, — параллелограмм.

24. Ромб.

25. 150 см².

Указание. Использовать пропорциональные отрезки в прямоугольном треугольнике.

26. 42 см и 56 см.

Указание. Точка, равноудаленная от сторон угла, принадлежит биссектрисе угла.

Биссектриса треугольника делит сторону на части, пропорциональные прилежащим сторонам. В данном случае отношение катетов равно 3 : 4. Применяя теорему Пифагора, получим уравнение (3x)² + (4x)² = 4900. х = 14.

27. 54 см².

Указание. Биссектриса треугольника делит сторону на части, пропорциональные прилежащим сторонам. В данном случае отношение катета и гипотенузы равно 4/5. Применяя теорему Пифагора, получим уравнение (5x)² - (4x)² = 9². х = 3.

28. 3 м.

Указание. Дополнительное построение: AM — высота треугольника АВС. Треугольники АМС и КНС подобны.

Дополнительные задачи. Тема № 4. Окружность

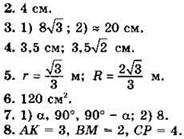
Указание. АK равно 1/2(Р - ВС), где Р — периметр треугольника.

9. Указание. Если четырехугольник вписан в окружность, то сумма противолежащих углов равна 180°.

Примените признак подобия треугольников по двум углам.

12. 16 см.

13. 16 см.

21. 20°, 30°, 130°; 30°, 40°, 110°; 40°, 20°, 120°.

23. 4 см, 4 см.

24. 1) 120 см², 2) 4 см, 13 см.

Решение. x см — длина одного катета, (34 - x) см — длина другого катета.

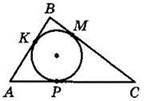
По теореме Пифагора х² + (34 - х)² = 26². Отсюда х = 10 или х = 24.

25. 10 см, 8 см и 6 см.

Указание. Отрезки касательных, проведенных из одной точке к окружности, равны.

Решение.

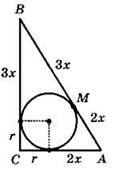
1) Треугольник АВС (угол С — прямой), М — точка касания окружности и гипотенузы, r — радиус вписанной окружности,

2) Применив формулу площади прямоугольного треугольника и теорему Пифагора, составим систему уравнений:

3) Решив систему, получим х = 2, r = 2.

26. 7,25 см.

Указание. Отрезки касательных, проведенных из одной точке к окружности, равны.

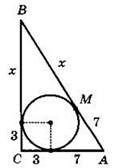
Решение.

1) Треугольник АВС (угол С прямой). АС = 3 + 7 (см), ВС = 3 + х (см), АВ = 7 + х (см).

2) По теореме Пифагора 100 + (3 + х)² = (7 + х)² х = 7,5.

3) АВ = 14,5 см, R = 7,25 см.

Решение.

1) Если диагональ ромба ABCD делит его на два равносторонних треугольника, то острый угол ромба — 60°.

2) Так как радиус вписанной окружности равен 2, то высота ромба и высота равностороннего треугольника равны 4.

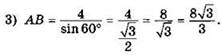
28. 120°.

Указание. Если в выпуклом четырехугольнике ABCD углы ABD и ACD равны, то около четырехугольника можно описать окружность.

29. 8.

Указание. Отрезки касательных, проведенных из одной точки к окружности, равны.

Биссектриса треугольника делит сторону на части, пропорциональные прилежащим сторонам.

Радиус, проведенный в точку касания, перпендикулярен касательной.

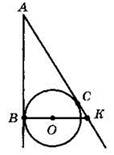
Решение.

1) АС = АВ = 8 см (по свойству касательных).

2) (по свойству биссектрисы треугольника).

3)

4) Треугольник АВК - прямоугольный.

5) Треугольник АВO – прямоугольный,

31. 10 см.

Дополнительные задачи. Тема № 5. Средняя линия трапеции

1. Неверно.

3. 54 см.

Указание. Биссектриса угла трапеции отсекает равнобедренный треугольник.

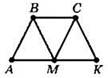
Решение.

1) Пусть АВСК — трапеция, АК — большее основание, СМ — биссектриса угла С, точка М — середина АК.

Треугольники АВМ и МСК — равнобедренные с основаниями ВМ и СМ соответственно.

2) Пусть половина меньшего основания равна х см, тогда АВ = AM = МК = СК = 14 - х (см). СН — высота трапеции и треугольника МСК.

3) В равнобедренном треугольнике МСК с основанием МС известно, что МН = х см, НК = 14 - 2х (см), СК = 14 - х (см), СН = 5 см. По теореме Пифагора для треугольника СНК (угол Н — прямой) получим (14 - х)² = 5² + (14 - 2х)², х = 1 (х = 25/3 не удовлетворяет условию).

4) Р = 13 + 13 + 13 + 13 + 2 = 54 см.

4. 12 см.

5. Указание. В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на два отрезка, длина большего из них равна полусумме оснований, меньшего — полуразности. 13 см.

6. 10,5 см.

7. 4/9 или 5/9.

Решение.

1) АВСК — трапеция, АК — большее основание, провели прямую СМ параллельно стороне АВ, которая разбила трапецию на ромб АВСМ и треугольник МСК, отношение площадей которых равно 4 : 5 или 5 : 4. Задача имеет два решения. Пусть ВС = AM = а, МК = b, h — высота трапеции. Средняя линия равна 0,5(2а + b).

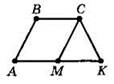
2) Пусть

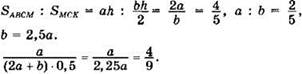
3) Пусть

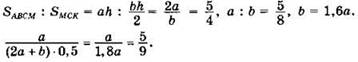
Решение.

Пусть основания трапеции равны а и b.

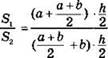
9. Указание. Через вершину тупого угла С трапеции ABCD провести прямую СК, параллельную диагонали BD. Треугольник АСК - прямоугольный (по теореме, обратной теореме Пифагора). Площадь трапеции равна половине произведения ее диагоналей. 120 см².