Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Контрольная работа № 8 по теме Формулы сокращенного умножения - ПРЕОБРАЗОВАНИЕ ЦЕЛЫХ ВЫРАЖЕНИЙ - ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
Ход урока
I. Сообщение темы и цели урока
II. Общая характеристика контрольной работы
Контрольная работа составлена в шести вариантах (варианты 1, 2 — самые простые, варианты 3, 4 — средней сложности, варианты 5, 6 — самые сложные). Степень сложности меняется не слишком резко, поэтому можно рекомендовать следующий критерий оценки: при выполнении вариантов 1, 2 оценка “3” ставится за любые три решенные задачи, оценка “4” — за четыре задачи и оценка “5” — за пять задач. Одна задача дает учащимся некоторую свободу выбора. При тех же критериях оценки за решение задач вариантов 3, 4 к набранным баллам добавляются дополнительно 0,5 балла, за решение задач вариантов 5, 6 — дополнительно 1 балл (т. е. оценка “5” выставляется уже за четыре задачи). Все задачи в варианте примерно равноценны. Возможно, несколько труднее для учеников задачи 5, 6.
Перед проведением контрольной работы учащихся целесообразно ознакомить с критериями оценки и разной сложностью вариантов. Выбор вариантов может быть осуществлен учителем или предоставлен ученикам (в этом случае предполагается наличие копировальной техники в школе и избыточное количество заданий). При наличии такой техники в классе на стенде (после контрольной) может быть вывешено решение всех задач шести вариантов.
Контрольная работа рассчитана на один урок.
III. Контрольная работа
Вариант 1
1. Запишите в виде многочлена стандартного вида выражение:
![]()
2. Разложите на множители многочлен:

3. Решите уравнение ![]()
4. Докажите, что выражение ![]() может принимать только неотрицательные значения.
может принимать только неотрицательные значения.
5. Постройте график функции ![]()
6. Докажите, что число 144 - 1452 кратно 3 и 17.
Вариант 2
1. Запишите в виде многочлена стандартного вида выражение:
![]()
2. Разложите на множители многочлен:
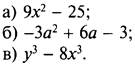
3. Решите уравнение ![]()
4. Докажите, что выражение ![]() может принимать только неотрицательные значения.
может принимать только неотрицательные значения.
5. Постройте график функции ![]()
6. Докажите, что число 154 - 1682 кратно 3 и 19.
Вариант 3
1. Запишите в виде многочлена стандартного вида выражение:
![]()
2. Разложите на множители выражение:
![]()
3. Решите уравнение ![]()
4. Найдите наименьшее значение выражения ![]()
5. Постройте график функции ![]()
6. Докажите, что число ![]() кратно 31.
кратно 31.
Вариант 4
1. Запишите в виде многочлена стандартного вида выражение:
![]()
2. Разложите на множители выражение:
![]()
3. Решите уравнение ![]()
4. Найдите наименьшее значение выражения ![]()
5. Постройте график функции ![]()
6. Докажите, что число ![]() кратно 39.
кратно 39.
Вариант 5
1. Запишите в виде многочлена стандартного вида выражение:
![]()
2. Разложите на множители выражение:
![]()
3. Решите уравнение ![]()
4. Найдите наибольшее значение выражения ![]()
5. Постройте график функции ![]()
6. При любом натуральном значении n найдите остаток от деления значения выражения ![]() на 6.
на 6.
Вариант 6
1. Запишите в виде многочлена стандартного вида выражение:
![]()
2. Разложите на множители выражение:
![]()
3. Решите уравнение ![]()
4. Найдите наибольшее значение выражения ![]()
5. Постройте график функции ![]()
6. При любом натуральном значении п найдите остаток от деления выражения ![]() на 6.
на 6.
IV. Подведение итогов контрольной работы
1. Распределение работ по вариантам и результаты решения. Удобно данные заносить в таблицу (для каждой пары вариантов).
|
№ задачи |
Итоги |
|||
|
+ |
± |
- |
Ø |
|
|
1 |
5 |
1 |
1 |
1 |
|
2 |
||||
|
... |
||||
|
6 |
||||
Обозначения:
+ — число решивших задачу правильно или почти правильно;
± — число решивших задачу со значительными погрешностями;
- — число не решивших задачу;
Ø — число не решавших задачу.
Варианты 1, 2 — 8 учащихся.
2. Типичные ошибки при решении задач.
3. Задачи, вызвавшие наибольшие трудности.
V. Разбор задач (ответы и решения)
Вариант 1
![]()
3. х = -3.
4. Доказано.
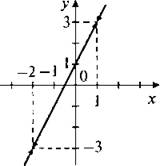
5. Прямая у = х - 2, х ≠ -1.
6. Доказано.
Вариант 2
![]()
3. х = -6.
4. Доказано.
5. Прямая у = х + 2, х ≠ 1.
6. Доказано.
Вариант 3
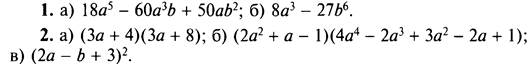
3. х = 1.
4. 7.
5. Прямая у = 2х + 1, х ≠ -2.
6. Доказано.
Вариант 4
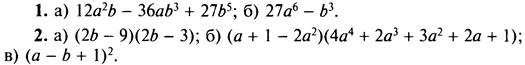
3. х = 3.
4. 6.
5. Прямая у = 2х - 1, x ≠ 2.
6. Доказано.
Вариант 5
1. Используем формулы сокращенного умножения и преобразуем данное выражение в многочлен стандартного вида.
а) Применяя формулу куба суммы, получим ![]()
![]()
б) В выражении (а + b + 2)2 будем рассматривать сумму а + b как одно число и используем формулу квадрата суммы. Получаем
![]()
в) В выражении (-3x - 2у)(3х - 2у) вынесем множитель (-1) из первого множителя и применим формулу разности квадратов. Получаем

2. Используем формулы сокращенного умножения и разложим выражение на множители.
а) Воспользуемся формулой разности квадратов и получим
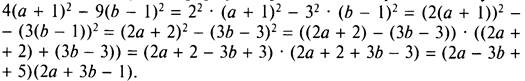
б) Сгруппируем члены в данном выражении и используем формулы квадрата разности и разности квадратов. Получаем

3. Преобразуем уравнение ![]()
![]() Для этого используем формулы куба суммы и разности квадратов и получим
Для этого используем формулы куба суммы и разности квадратов и получим ![]() или
или ![]()
Приведем подобные члены: 12х + 9 = 0, отсюда ![]()
(Ответ: x = -3/4.)
4. В данном выражении выделим квадрат разности. Для этого член -2у2 представим в виде -у2 - у2 и сгруппируем члены. Получаем
![]()
Данное выражение представляет собой разность числа 7 и двух неотрицательных величин у2 и (у - 2х)2. Очевидно, что данное выражение будет наибольшим, если вычитаемые величины минимальны (т. е. равны нулю), откуда у = 0 и у - 2х = 0 (тогда х = y/2 = 0).
Итак, при х = у = 0 данное выражение имеет наибольшее значение, равное 7.
(Ответ: 7.)
5. При построении графика функции ![]() учтем, что знаменатели дробей не равны нулю (т. е. х - 1 ≠ 0 и х + 2 ≠ 0), откуда х ≠ 1 и х ≠ -2. Числитель первой дроби является квадратом разности, числитель второй дроби — квадратом суммы. Поэтому можно сократить дроби. Получаем
учтем, что знаменатели дробей не равны нулю (т. е. х - 1 ≠ 0 и х + 2 ≠ 0), откуда х ≠ 1 и х ≠ -2. Числитель первой дроби является квадратом разности, числитель второй дроби — квадратом суммы. Поэтому можно сократить дроби. Получаем
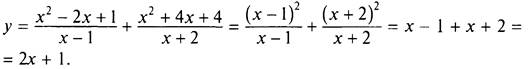
Итак, строим график линейной функции у = 2х + 1 (прямая линия). Удаляем из этого графика две точки с абсциссами х = 1 и х = -2 (показаны стрелками).
6. Используя формулу разности квадратов, преобразуем данное выражение: ![]()
![]()
Так как при всех натуральных п выражение 6п кратно 6, то остаток от деления выражения 6n + 9 на 6 равен остатку от деления числа 9 на число 6. Такой остаток равен 3.
(Ответ: 3.)
Вариант 6
1. Используем формулы сокращенного умножения и преобразуем данное выражение в многочлен стандартного вида.
а) Применяя формулу куба суммы, получим ![]()
![]()
б) В выражении (2а + b + 1)2 будем рассматривать сумму 2а + b как одно число и использовать формулу квадрата суммы. Получаем
![]()
![]()
в) В выражении (-2х - 5у)(2х - 5у) вынесем множитель (-1) из первого множителя и применим формулу разности квадратов. Получаем

2. Используя формулы сокращенного умножения, разложим выражение на множители.
а) Воспользуемся формулой разности квадратов и получим:
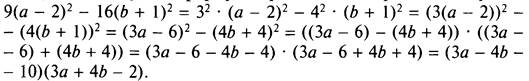
б) Сгруппируем члены в данном выражении и используем формулы квадрата разности и разности квадратов. Получаем
![]()
![]()
3. Преобразуем уравнение (х - 1)3 - х2(х - 4) - (х - 2)(х + 2) = 0. Для этого используем формулы куба суммы и разности квадратов и получаем ![]() или
или ![]()
Приведем подобные члены: 3х + 3 = 0, откуда х = -1.
(Ответ: х = -1.)
4. В данном выражении выделим квадрат разности. Для этого член -5у2 представим в виде -у2 - 4у2 и сгруппируем члены. Получаем
![]()
Данное выражение представляет собой разность числа 5 и двух неотрицательных величин у2 и (2у - 3х)2. Очевидно, что данное выражение будет наибольшим, если вычитаемые величины минимальны (т. е. равны нулю), откуда у = 0 и 2у - 3х = 0 (тогда х = 2/3 у = 0).
Итак, при х = у = 0 данное выражение имеет наибольшее значение, равное 5.
(Ответ: 5.)
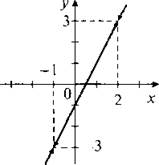
5. При построении графика функции ![]() учтем, что знаменатели дробей не равны нулю (т. е. х + 1 ≠ 0 и х - 2 ≠ 0), откуда х ф -1 и х * 2. Числитель первой дроби является квадратом суммы, числитель второй дроби — квадратом разности. Поэтому можно сократить дроби. Получаем
учтем, что знаменатели дробей не равны нулю (т. е. х + 1 ≠ 0 и х - 2 ≠ 0), откуда х ф -1 и х * 2. Числитель первой дроби является квадратом суммы, числитель второй дроби — квадратом разности. Поэтому можно сократить дроби. Получаем
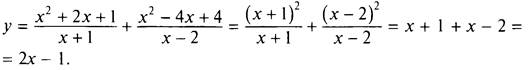
Итак, строим график линейной функции у = 2х - 1 (прямая линия). Удаляем из этого графика две точки с абсциссами х = -1 и х = 2 (показаны стрелками).
6. Используя формулу разности квадратов, преобразуем данное выражение:
![]()
Так как при всех натуральных n выражение 6n кратно 6, то остаток от деления выражения 6n + 9 на 6 равен остатку от деления числа 9 на число 6. Такой остаток равен 3.
(Ответ: 3.)
VI. Подведение итогов урока