Поурочные разработки по алгебре 7 класс - к учебнику Ю.Н. Макарычева - 2014 год
Зачет по теме Функции - ЛИНЕЙНАЯ ФУНКЦИЯ - ФУНКЦИИ
Цели: сравнить успеваемость учащихся при одинаковой сложности заданий; иметь возможность повысить оценки за выполненные контрольные работы.
Тип уроков: урок контроля, оценки и коррекции знаний.
Ход уроков
I. Сообщение темы и целей уроков
II. Общая характеристика зачетной работы
Работа составлена в двух равноценных вариантах. По сравнению с контрольной работой увеличено количество заданий. Соответственно, у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В и С. Самые простые задачи представлены в блоке А, более сложные — в блоке В, еще сложнее — в блоке С. Каждая задача из блока А оценивается 1 баллом, из блока В — 2 баллами, из блока С — 3 баллами. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В — 8 баллов и блока С — 9 баллов (всего 24 балла). Оценка “3” ставится за 6 баллов, оценка “4” — за 10 баллов, оценка “5” — за 14 баллов.
Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Работа рассчитана на два урока.
III. Зачетная работа
Вариант 1
А
1. Дана функция у = 2х - 3. Найдите:
а) значение функции при х = -1;
б) значение аргумента, при котором значение функции у = -7.
2. Определите точки пересечения графика функции у = -3х + 5 с осями координат.
3. Принадлежит ли графику функции у = 3х - |х| + 1 точка:
а) А (-1; -3);
б) В (2; 4)?
4. Постройте график функции ![]()
5. Постройте график функции у = kх и определите угловой коэффициент k, если график проходит через точку А (-6; -3).
6. Поезд первоначально находится на расстоянии 30 км от города и удаляется от него со скоростью 40 км/ч. Задайте формулой расстояние s от города до поезда в зависимости от времени движения t.
7. График функции параллелен прямой у = 3х - 7 и проходит через точку А (2; 1). Задайте формулой эту функцию.
В
8. Определите точки пересечения графика функции ![]() с осями координат.
с осями координат.
9. Найдите точку пересечения графиков функций у = 5х - 3 и у = 7х - 19.
10. Постройте график функции ![]()
11. Постройте график уравнения |2х - 4| + |у - 3| = 0.
С
12. Графики функций у = (2a - 3) ∙ x + a – 7 и y = (4 а - 1) ∙ х + 5 - 3а параллельны. Найдите значение параметра а и формулу каждой функции.
13. Постройте график функции ![]()
14. Постройте график уравнения |у - х| + х = 2.
Вариант 2
А
1. Дана функция у = 3х - 4. Найдите:
а) значение функции при х = -1;
б) значение аргумента, при котором значение функции у = -10.
2. Определите точки пересечения графика функции у = -2х + 7 с осями координат.
3. Принадлежит ли графику функции у = 4х - |х| + 2 точка:
а) А (-1; -3);
б) В (2; 6)?
4. Постройте график функции ![]()
5. Постройте график функции у = kх и определите угловой коэффициент k, если график проходит через точку А (-3; -6).
6. Поезд первоначально находится на расстоянии 40 км от города и удаляется от него со скоростью 30 км/ч. Задайте формулой расстояние s от города до поезда в зависимости от времени движения t.
7. График функции параллелен прямой у = 2х - 6 и проходит через точку А (3; 2). Задайте формулой эту функцию.
В
8. Определите точки пересечения графика функции ![]() с осями координат.
с осями координат.
9. Найдите точку пересечения графиков функций у = 3х - 14 и у = 5х - 6.
10. Постройте график функции ![]()
11. Постройте график уравнения |4 - 2х| + |у - 1| = 0.
С
12. Графики функций у = (3а + 2) ∙ x + 2а - 1 и у = (а - 2) ∙ x + 3 - 4а параллельны. Найдите значение параметра а и формулу каждой функции.
13. Постройте график функции ![]()
14. Постройте график уравнения |у + x| - х = 3.
IV. Разбор задач (ответы и решения)
Вариант 1
А
1. Дана функция у = 2х - 3.
а) Найдем значение функции при х = -1. Для этого в формулу функции вместо х подставим число -1 и получим у= 2 ∙ (-1) - 3 = -2 - 3 = -5.
б) Найдем значение аргумента, при котором значение функции у = -7. Для этого в формулу функции вместо у подставим число -7 и получим линейное уравнение -7 = 2х - 3 или -4 = 2х, откуда х = -2.
(Ответы: а) у = -5; б) х - -2.)
2. Найдем точки пересечения графика функции у = -3х + 5 с осями координат. Сначала определим точку пересечения с осью ординат. Так как любая точка на оси ординат имеет нулевую абсциссу, то подставим значение x = 0 в формулу функции и получим у = -3 ∙ 0 + 5 = 5. Итак, точка пересечения с осью ординат имеет координаты А (0; 5).
Найдем точку пересечения графика с осью абсцисс. Так как любая точка на оси абсцисс имеет нулевую ординату, то подставим значение у = 0 в формулу функции и получим линейное уравнение 0 = -3x + 5 или 3х = 5, откуда х = 5/3. Итак, точка пересечения с осью абсцисс имеет координаты B (5/3; 0).
(Ответ: А (0; 5), B (5/3; 0).)
3. Для функции у = 3х - |x| + 1 найдем значение функции при значении аргумента, равном абсциссе данной точки.
а) При х = -1 получаем у = 3 ∙ (-1) - |-1| + 1 = -3 - 1 + 1 = -3. Так как значение функции равно ординате точки А (-1; -3), то точка А принадлежит графику функции.
б) При х = 2 получаем у = 3 ∙ 2 - |2| + 1 = 6 – 2 + 1 = 5. Так как значение функции не равно ординате точки В (2; 4), то точка В не принадлежит графику функции.
(Ответ: точка А принадлежит, В - не принадлежит.)
4. При построении графика функции ![]() учтем, что х ≠ 0. Умножим обе части данного равенства на х и получим у = -2х - 2. Построим график этой линейной функции, определив, например, точки пересечения графика с осями координат.
учтем, что х ≠ 0. Умножим обе части данного равенства на х и получим у = -2х - 2. Построим график этой линейной функции, определив, например, точки пересечения графика с осями координат.

Из графика удалим точку А, абсцисса которой равна нулю (эта точка показана стрелками).
5. На координатной плоскости построим точку А (-6; -3).

Так как функция у = kх — прямая пропорциональная зависимость, то ее график проходит через начало координат. Поэтому через начало координат и точку А проведем прямую — график данной функции. Так как график проходит через точку А, то ее координаты удовлетворяют уравнению функции. Поэтому получаем -3 = k(-6), откуда k = ½.
(Ответ: k = 1/2.)
6. Пусть первоначально поезд находится в точке В на расстоянии 30 км от города (точка А).
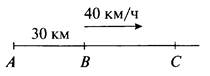
Двигаясь со скоростью 40 км/ч, поезд за время t ч преодолеет расстояние ВС = 40t. Тогда расстояние поезда от города s = АС = АВ + ВС = 30 + 40/ км.
(Ответ: s = 30 + 40t.)
7. Так как график функции параллелен прямой у = 3х - 7, то угловой коэффициент данной функции такой же (т. е. k = 3). Поэтому функция имеет вид у = 3х + b. Найдем величину b. Так как график функции проходит через точку А (2; 1), то ее координаты удовлетворяют уравнению функции 1 = 3 ∙ 2 + b или 1 = 6 + b), откуда b = -5. Итак, искомая функция у = 3х - 5.
(Ответ: у = 3х - 5.)
В
8. Определим точки пересечения графика функции ![]() с осями координат. Точка пересечения с осью ординат имеет абсциссу, равную нулю. Поэтому подставим значение х = 0 в функцию и получим
с осями координат. Точка пересечения с осью ординат имеет абсциссу, равную нулю. Поэтому подставим значение х = 0 в функцию и получим ![]() Итак, координаты точки пересечения с осью ординат А (0; -4). Точка пересечения с осью абсцисс имеет нулевую ординату. Поэтому подставим значение у = 0 в функцию и получим уравнение
Итак, координаты точки пересечения с осью ординат А (0; -4). Точка пересечения с осью абсцисс имеет нулевую ординату. Поэтому подставим значение у = 0 в функцию и получим уравнение ![]() Дробь равна нулю, если ее числитель равен нулю: 0 = 2х - 4 (а знаменатель при этом в нуль не обращается), откуда х = 2. Итак, координаты точки пересечения с осью абсцисс В (2; 0).
Дробь равна нулю, если ее числитель равен нулю: 0 = 2х - 4 (а знаменатель при этом в нуль не обращается), откуда х = 2. Итак, координаты точки пересечения с осью абсцисс В (2; 0).
(Ответ: А (0; -4), В (2; 0).)
9. Пусть A (x0; у0) — точка пересечения графиков функций у = 5х - 3 и у = 7х - 19. Эта точка принадлежит каждому графику, и ее координаты удовлетворяют каждой функции, т. е. выполняются равенства у0 = 5х0 - 3 и у0 = 7х0 - 19. Так как левые части одинаковы, то равны и правые части. Получаем линейное уравнение 5х0 - 3 = 7х0 - 19 или 16 = 2х0, откуда абсцисса точки пересечения х0 = 8. Теперь из любого равенства, например из первого, найдем ординату: у0 = 5х0 - 3 = 5 ∙ 8 - 3 = 40 - 3 = 37. Итак, координаты точки пересечения А (8; 37).
(Ответ: А (8; 37).)
10. Построим график данной функции.
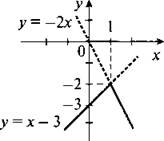
Сначала строим график функции у = х - 3 и выбираем из него те точки, абсциссы которых х ≤ 1 (сплошная линия). Потом строим график функции у = -2х и выбираем из него те точки, абсциссы которых х > 1 (сплошная линия).
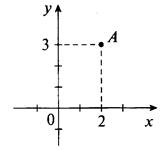
11. Так как модуль любого выражения — величина неотрицательная, то уравнение |2х - 4| + |у - 3| = 0 выполняется только в том случае, если |2х - 4| = 0 и |у - 3| = 0. Модуль величины равен нулю, если сама величина равна нулю. Поэтому получаем уравнения 2х - 4 = 0 (откуда х = 2) и у - 3 = 0 (тогда у = 3). Итак, графиком данного уравнения является единственная точка А (2; 3).
С
12. Графики линейных функций у = kх + b параллельны, если выполнены условия: k1 = k2 и b1 ≠ b2. Для данных функций у = (2а - 3) ∙ х + а - 7 и у = (4а - 1) ∙ х + 5 - 3а получаем условия: 2а - 3 = 4а - 1 и а - 7 ≠ 5 - 3а. Решим уравнение 2а - 3 = 4а - 1. Получаем -2 = 2а, откуда а = -1. Проверим, что выполняется неравенство а - 7 ≠ -3а. Подставим значение а = -1 в левую и правую части и получим верное неравенство -1 – 7 ≠ 5 – 3 ∙ (-1) или -8 ≠ 8. Теперь подставим а = -1 в данные функции и определим их: у = (2 ∙ (-1) - 3) ∙ х + (-1) - 7 и у = (4 ∙ (-1) - 1) ∙ х + 5 - 3 ∙ (-1) или у = -5х - 8 и у = -5х + 8.
(Ответ: а = -1, у = -5х - 8, у = -5х + 8.)
13. Построим график функции ![]() Учтем, что х ≠ 0, и раскроем знак модуля. Если х < 0, то |х| = -х и функция имеет следующий вид:
Учтем, что х ≠ 0, и раскроем знак модуля. Если х < 0, то |х| = -х и функция имеет следующий вид: ![]() или у = -х - 1. Построим график этой функции при х < 0.
или у = -х - 1. Построим график этой функции при х < 0.

Если х > 0, то |х| = х и функция имеет следующий вид: ![]() или у = х + 1. Построим график этой функции при х > 0. Стрелками показано, что при х = 0 функция не определена (не имеет смысла).
или у = х + 1. Построим график этой функции при х > 0. Стрелками показано, что при х = 0 функция не определена (не имеет смысла).
14. Для построения графика уравнения |у - х| + х = 2 раскроем знак модуля, рассмотрев два случая.
1. Если у - х < 0, то |у - х| = -(у - х) = х - у и уравнение имеет вид х - у + х = 2, откуда у = 2х - 2. Подставим эту величину у в неравенство у - х < 0 и получим 2х - 2 - х < 0 или х - 2 < 0. Это неравенство выполняется при х ≤ 2. Построим график функции у = 2х - 2 при х < 2.
2. Если у – х ≥ 0, то |у - х| = у – х и уравнение имеет вид у - х + х = 2, откуда у = 2. Подставим эту величину у в неравенство у - х ≥ 0 и получим 2 - х ≥ 0. Это неравенство выполняется при х ≤ 2. Построим график функции у = 2 при х ≤ 2.
В результате рассмотрения двух случаев получаем график данного уравнения.

Вариант 2
А
1. Дана функция у = 3х - 4.
а) Найдем значение функции при x = -1. Для этого в формулу функции вместо х подставим число -1 и получим у = 3 ∙ (-1) - 4 = -3 - 4 = -7.
б) Найдем значение аргумента, при котором значение функции у = -10. Для этого в формулу функции вместо у подставим число -10 и получим линейное уравнение -10 = 3х - 4 или -6 = 3х, откуда х = -2.
(Ответы: а) у = -7; б) х = -2.)
2. Найдем точки пересечения графика функции у = -2x + 7 с осями координат. Так как любая точка на оси ординат имеет нулевую абсциссу, то подставим значение х = 0 в формулу функции и получим у = -2 ∙ 0 + 7 = 7. Итак, точка пересечения с осью ординат имеет координаты А (0; 7).
Найдем точку пересечения графика с осью абсцисс. Так как любая точка на оси абсцисс имеет нулевую ординату, то подставим значение у = 0 в формулу функции и получим линейное уравнение 0 = -2х + 7 или 2х = 7, откуда х = 3,5. Итак, точка пересечения с осью абсцисс имеет координаты В (3,5; 0).
(Ответ: А (0; 7), В (3,5; 0).)
3. Для функции у = 4х - |х| + 2 найдем значение функции при значении аргумента, равном абсциссе данной точки.
а) При х = -1 получаем у = 4 ∙ (-1) - |-1| + 2 = -4 - 1 + 2 = -3. Так как значение функции равно ординате точки А (-1; -3), то точка А принадлежит графику функции.
б) При х = 2 получаем у = 4 ∙ 2 - |2| + 2 = 8 - 2 + 2 = 8. Так как значение функции не равно ординате точки В (2; 6), то точка В не принадлежит графику функции.
(Ответ: точка А принадлежит, В — не принадлежит.)
4. При построении графика функции ![]() учтем, что х ≠ 0. Умножим обе части данного равенства на х и получим у = -3х - 1. Построим график этой линейной функции, определив, например, точки пересечения графика с осями координат.
учтем, что х ≠ 0. Умножим обе части данного равенства на х и получим у = -3х - 1. Построим график этой линейной функции, определив, например, точки пересечения графика с осями координат.
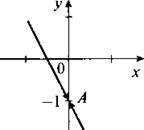
Из графика удалим точку А, абсцисса которой равна нулю (эта точка показана стрелками).
5. На координатной плоскости построим точку А (-3; -6). Так как функция у = kх — прямая пропорциональная зависимость, то ее график проходит через начало координат. Поэтому через начало координат и точку А проведем прямую — график данной функции.
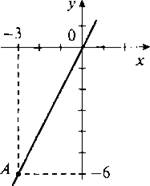
Так как график проходит через точку А, то ее координаты удовлетворяют уравнению функции. Поэтому получаем -6 = k(-3), откуда k = 2.
(Ответ: k = 2.)
6. Пусть первоначально поезд находится в точке В на расстоянии 40 км от города (точка А).
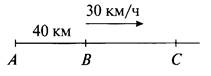
Двигаясь со скоростью 30 км/ч, поезд за время t ч преодолеет расстояние ВС = 30t. Тогда расстояние поезда от города s = АС = АВ + ВС = 40 + 30/ км.
(Ответ: s = 40 + 30t.)
7. Так как график функции параллелен прямой у = 2х - 6, то угловой коэффициент данной функции такой же (т. е. k = 2). Поэтому функция имеет вид у = 2х + b. Найдем величину b. Так как график функции проходит через точку А (3; 2), то ее координаты удовлетворяют уравнению функции: 2 = 2 ∙ 3 + b или 2 = 6 + b, откуда b = -4. Итак, искомая функция у = 2х - 4.
(Ответ: у = 2х - 4.)
В
8. Определим точки пересечения графика функции ![]() с осями координат. Точка пересечения с осью ординат имеет абсциссу, равную нулю. Поэтому подставим значение х = 0 в функцию и получим
с осями координат. Точка пересечения с осью ординат имеет абсциссу, равную нулю. Поэтому подставим значение х = 0 в функцию и получим ![]() Итак, координаты точки пересечения с осью ординат A (0; -3). Точка пересечения с осью абсцисс имеет нулевую ординату. Поэтому подставим значение у = 0 в функцию и получим уравнение
Итак, координаты точки пересечения с осью ординат A (0; -3). Точка пересечения с осью абсцисс имеет нулевую ординату. Поэтому подставим значение у = 0 в функцию и получим уравнение ![]() Дробь равна нулю, если ее числитель равен нулю: 0 = 3х - 6 (а знаменатель при этом в нуль не обращается), откуда х = 2. Итак, координаты точки пересечения с осью абсцисс В (2; 0).
Дробь равна нулю, если ее числитель равен нулю: 0 = 3х - 6 (а знаменатель при этом в нуль не обращается), откуда х = 2. Итак, координаты точки пересечения с осью абсцисс В (2; 0).
(Ответ: А (0; -3), В (2; 0).)
9. Пусть А (х0; у0) — точка пересечения графиков функций у = 3х - 14 и у = 5х - 6. Эта точка принадлежит каждому графику, и ее координаты удовлетворяют каждой функции, т. е. выполняются равенства у0 = 3х0 - 14 и у0 = 5х0 - 6. Так как левые части одинаковы, то равны и правые части. Получаем линейное уравнение 3х0 - 14 = 5х0 - 6 или -8 = 2х0, откуда абсцисса точки пересечения х0 = -4. Теперь из любого равенства, например из первого, найдем ординату: у0 = 3х0 - 14 = 3- (-4) - 14 = -12 - 14 = -26. Итак, координаты точки пересечения А (-4; -26).
(Ответ: А (-4; -26).)
10. Построим график данной функции.

Сначала строим график функции у = х + 1 и выбираем из него те точки, абсциссы которых х ≤ 1 (сплошная линия). Потом строим график функции у = 2х и выбираем из него те точки, абсциссы которых х > 1 (сплошная линия).
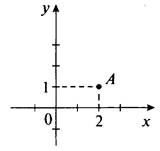
11. Так как модуль любого выражения — величина неотрицательная, то уравнение |4 - 2х| + |у - 1| = 0 выполняется только в том случае, если |4 - 2х| = 0 и |у - 1| = 0. Модуль величины равен нулю, если сама величина равна нулю. Поэтому получаем уравнения 4 - 2х = 0 (откуда х = 2) и у – 1 = 0 (тогда у = 1). Итак, графиком данного уравнения является единственная точка А (2; 1).
С
12. Графики линейных функций у = kх + b параллельны, если выполнены условия: k1 = k2 и b1 ≠ b2 Для данных функций у = (3а + 2) ∙ х + 2а - 1 и у = (а - 2) ∙ х + 3 - 4а получаем условия: 3а + 2 = а - 2 и 2а - 1 ≠ 3 - 4а. Решим уравнение 3а + 2 = а - 2. Получаем 2а = -4, откуда а = -2. Проверим, что выполняется неравенство 2а - 1 ≠ 3 - 4а. Подставим значение а = -2 в левую и правую части и получим верное неравенство 2 ∙ (-2) – 1 ≠ 3 - 4 ∙ (-2) или -5 ≠ 11. Теперь подставим а = -2 в данные функции и определим их: у = (3 ∙ (-2) + 2) ∙ х + 2 ∙ (-2) - 1 и у = (-2 - 2) ∙ х + 3 - 4 ∙ (-2) или у = -4х - 5 и у = -4х + 11.
(Ответ: а = -2, у = -4х - 5, у = -4х + 11.)
13. Построим график функции ![]() Учтем, что х ≠ 0, и раскроем знак модуля. Если х < 0, то |х| = -х и функция имеет следующий вид:
Учтем, что х ≠ 0, и раскроем знак модуля. Если х < 0, то |х| = -х и функция имеет следующий вид: ![]() или у = -х + 1. Построим график этой функции при х < 0.
или у = -х + 1. Построим график этой функции при х < 0.
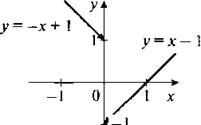
Если х > 0, то |х| = х и функция имеет следующий вид: ![]() или у = х - 1. Построим график этой функции при х > 0. Стрелками показано, что при х = 0 функция не определена (не имеет смысла).
или у = х - 1. Построим график этой функции при х > 0. Стрелками показано, что при х = 0 функция не определена (не имеет смысла).
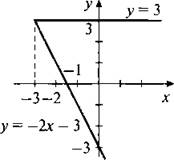
14. Для построения графика уравнения |у + х| - х = 3 раскроем знак модуля, рассмотрев два случая.
1. Если у + х < 0, то |у + х| = -(у + х) = -у - х и уравнение имеет вид -у - х - х = 3, откуда у = -2х - 3. Подставим эту величину у в неравенство у + х < 0 и получим -2х - 3 + х < 0 или -х - 3 < 0. Это неравенство выполняется при х > -3. Построим график функции у = -2х - 3 при х > -3.
2. Если у + х ≥ 0, то |у + х| = у + х и уравнение имеет вид у + х - х = 3, откуда у = 3. Подставим эту величину у в неравенство у + х ≥ 0 и получим 3 + х ≥ 0. Это неравенство выполняется при х ≥ -3. Построим график функции у = 3 при х ≥ - 3.
В результате рассмотрения двух случаев получаем график данного уравнения.
V. Подведение итогов уроков