Окружность и круг - Урок 2 - ОБЫКНОВЕННЫЕ ДРОБИ - ДРОБНЫЕ ЧИСЛА

Основная дидактическая цель урока: учить строить окружности по заданному радиусу и диаметру; совершенствовать вычислительные навыки; продолжить работу над текстовыми задачами.

Ход урока

I. Организационный момент

II. Устный счет

С. 135. № 860 (вычислите по цепочке).

(Внимание! В учебнике опечатка в 4-й цепочке. Вместо “: 7” надо читать “: 70”.)

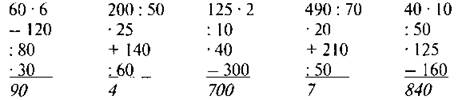
— Сколькими разными способами можно поставить в колонну по одному 6 человек? (6! = 720.)

III. Определение темы урока

— Разгадайте кроссворд.

По горизонтали:

1) Ч1асть плоскости, ограниченная окружностью. (Круг.)

2) Отрезок, соединяющий две точки окружности и проходящий через ее центр. (Диаметр.)

3) Часть окружности, ограниченная двумя точками. (Дуга.)

4) Отрезок, соединяющий две любые точки окружности. (Хорда.)

5) Отрезок, соединяющий центр окружности с любой ее точкой. (Радиус.)

6) Точка, в которую устанавливают иголку циркуля для построения окружности. (Центр.)

— Прочитайте слово по вертикали.

— Сформулируйте тему урока.

— Чему равен радиус окружности, если диаметр 12 см, 6 м, 44 дм, 18 см?

— Чему равен диаметр окружности, если радиус 5 мм, 16 см, 9 дм, 10 м?

IV. Работа по теме урока

1. С. 134, № 853.

— Какой вывод можно сделать, если расстояние от центра окружности до точки больше радиуса? меньше радиуса?

— Как расположен отрезок СМ по отношению к окружности О, если расстояния от центра окружности до точек С и М меньше радиуса? больше радиуса? равны радиусу?

2. С. 134, № 854 (устно) (работа в паре).

3. С. 134, № 855.

4. С. 134, № 856.

— Прочитайте задачу. Сравните ее с предыдущей.

— Что вы заметили?

— Кто догадался, как выполнить это задание?

(Обсуждение предложений учащихся.)

V. Повторение изученного материала. Решение задач

С. 137, № 871.

— Какой путь решения выберем?

— Что обозначим через х!

— Прочитайте вопрос задачи.

Пусть первоначально на крыше сидело х голубей.

Когда сели еще 15, голубей стало x + 15.

Когда 18 улетели, голубей осталось (х + 15) — 18.

По условию голубей осталось 16.

Значит, можем составить уравнение:

(х + 15) - 18 = 16

х + 15 = 16 + 18

х + 15 = 34

х = 34 — 15

х = 19 (голубей) — первоначально было на крыше.

— Прочитайте вторую задачу. Сравните ее с первой.

— Что можете сказать о ней?

— Решите самостоятельно.

Проверка

Пусть первоначально в составе было х вагонов.

Когда отцепили 6 вагонов, их стало х — 6.

После того как прицепили 19 вагонов, их стало (х — 6) + 19.

А по условию задачи вагонов стало 50.

Значит, можем составить уравнение:

(х — 6) + 19 = 50

х — 6 = 50 — 19

х — 6 = 31

х = 31 + 6

х = 37 (вагонов) — стало в товарном составе.

VI. Рефлексия

— Оцените свою работу на уроке.

— Можно ли диаметр назвать хордой?

— Есть ли хорда больше, чем диаметр?

— Можно ли любую хорду назвать диаметром? Объясните почему.

Домашнее задание

С. 137, № 876, 877, 878 (в, г).