Упрощение выражений - Урок 5 - УМНОЖЕНИЕ И ДЕЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ - НАТУРАЛЬНЫЕ ЧИСЛА

Основная дидактическая цель урока: совершенствовать умение учащихся выполнять упрощение выражений; продолжить работу над задачами, которые решают с помощью составления уравнений.

Ход урока

I. Организационный момент

II. Устный счет. Определение темы урока

Для выражений из левого столбика найдите пару из правого. Соедините их стрелочками.

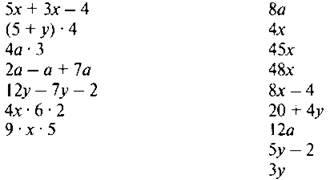
— Какие выражения остались без пары?

— Как вы думаете, почему я их включила?

— Какие свойства умножения применяют при упрощении выражений?

— Для чего нужно хорошо уметь упрощать выражения, где это пригодится? (При решении уравнении и задач.)

— Сформулируйте тему урока.

III. Решение задач

1. С. 89, № 587 (работа в паре).

Проверка

Пусть масса одной части будет x.

Масса воды будет 7х.

Масса молочного жира будет 2х.

Масса сахара будет 2x.

Масса всего состава равна 7х + 2х + 2х.

А в условии сказано, что масса мороженого 4400 кг.

Значит, можем составить уравнение:

7х + 2x + 2x = 4400

11x = 4400

x = 4400 : 11

x = 400 (кг) — масса одной части.

2x = 400 ∙ 2 = 800 (кг) — потребуется сахара.

— Сосчитайте устно, сколько потребуется воды и молочного жира.

2. С. 89, № 588.

— Прочитайте задачу.

— Эта задача на части?

— О чем говорится в задаче?

— Что сказано про количество домов на одной улице?

— Что еще известно?

— Что следует обозначить через x?

— Прочитайте вопрос.

— Сколько неизвестных в вопросе?

— Как поступить в этом случае?

Пусть на одной стороне улицы было x домов.

Тогда на другой стороне улицы их было 2x.

На двух сторонах улицы вместе домов было x + 2x.

Когда построили еще 12 домов, то всего домов стало x + 2x + 12. А в условии задачи сказано, что домов стало 99.

Значит, можем составить уравнение:

x + 2x + 12 = 99

3x + 12 = 99

3x = 99 — 12

3x = 87

x = 87 : 3

x = 29 (домов) — было на одной стороне улицы.

2x = 29 ∙ 2 = 58 (домов) — на другой стороне улицы.

3. С. 89, № 584.

— Прочитайте задачу.

— Эта задача на части?

— Решите ее самостоятельно.

Проверка

Пусть масса одной части будет x.

Масса муки будет 6x.

Масса отрубей будет 2x.

Общая масса всего зерна равна 6x + 2x.

А в условии сказано, что зерна было 1000 кг. Значит, можем составить уравнение:

6х + 2х = 1000

8x = 1000

x = 1000 : 8

x = 125 (кг) — отрубей.

6x = 125 ∙ 6 = 750 (кг) — муки.

IV. Учимся думать

1. С. 90, № 595 (устно).

2. С. 90, № 596 (устно).

Ответ: 1 + 1 + 1 + 2 + 5 = 1 ∙ 1 ∙ 1 ∙ 2 ∙ 5 = 10.

3. С. 90, № 598.

— Прочитайте задачу.

— Что вы можете сказать про эту задачу?

— Сколько вариантов выбора первой цифры существует? (10.)

— Сколько вариантов выбора второй, третьей, четвертой цифр?

— Сколько различных вариантов кода? (10 ∙ 10 ∙ 10 ∙ 10 = 10 000.)

V. Повторение. Решение уравнений

С. 90, № 601 (работа в паре).

VI. Рефлексия

— Оцените свое настроение, поясните.

— Где применяется упрощение выражений?

— Какие свойства используют при упрощении выражений?

Домашнее задание

С. 92, № 622, 625 (б, в).