Поурочные разработки по Математике 5 класс к УМК Н.Я. Виленкина
Деление на десятичную дробь - Урок 5 - УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ - ДРОБНЫЕ ЧИСЛА
Основная дидактическая цель урока: совершенствовать умение выполнять деление на десятичную дробь и числа 0,1; 0,01; 0,001; продолжить работу над текстовыми задачами.
Ход урока
I. Организационный момент
II. Определение темы урока
На доске:
12,3 9,15 0,33 27,3 6,21
— Прочитайте числа.
— Каждое из этих чисел разделите на 0,03; 0,3; 3; 0,1; 0,01.
— Если вы догадались, как это сделать, то сформулируйте тему нашего урока.
III. Устный счет
— Сегодня вы узнаете название удивительного плода, который по вкусу напоминает смесь ананаса и груши. Для этого вам необходимо верно решить все примеры и буквы вписать в таблицу ответов.
![]()
3,213
101
0,24
71
7,631
0,006
19
0,28
Это джекфрут. Растет он в странах Южной и Юго-Восточной Азии от Индии до Индонезии. Плоды его имеют форму бочонка.
IV. Работа по теме урока
1. На доске:
![]()
— Если вы решите правильно эти примеры, то узнаете массу одного джекфрута в килограммах, его длину в сантиметрах и диаметр в метрах.
— Чему же равна масса этого удивительного плода? (36 кг.)
— Кто смог определить его длину? (90 см.)
— Назовите диаметр плода. (0,5 м.)
2. С. 222, № 1459 (в, г).
(z - 1,2) : 0,6 = 21,1
— Где находится неизвестное число?
— Как найти делимое?
— Что теперь неизвестно?
— Как найти уменьшаемое?
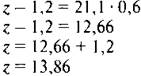
Ответ: 13,86.
3,5m + m = 9,9
— Что нужно сделать? (Упростить.)
— Какой коэффициент перед m?
![]()
Ответ: 2,2.
V. Решение задач
1. С. 222, № 1462.
— Что сказано о росте кенгуру?
— Что еще известно в задаче?
(Составление и запись условия задачи.)
![]()
— Кто же из животных ниже?
— Чей рост обозначим за х!
— Что такое 2,52 м? (Это разность.)
— Какое выражение надо составлять при решении? (Разность.)
— Решите задачу самостоятельно.
Проверка
Пусть рост кенгуру будет х.
Тогда рост жирафа будет 2,4x.
Жираф выше кенгуру на 2,4х — х.
А по условию задачи он выше на 2,52 м.
Значит, можем составить уравнение:
2,4х — x = 2,52
1,4x = 2,52
х = 2,52 : 1,4
х = 1,8 (м) — рост кенгуру.
1,8 ∙ 2,4 = 4,32 (м) — рост жирафа.
— Как иначе вычислить высоту жирафа? (1,8 + 2,52 = 4,32.)
2. С. 223, № 1463.
— С какими величинами эта задача?
— Чему равно расстояние между пешеходами?
— Что еще известно в задаче?
— Что можно узнать, зная расстояние и время? (Скорость сближения.)
— Найдите эту скорость.
4,6 : 0,8 = 5,75 (км/ч)
— Сформулируйте задачу, которая получилась. (Сумма скоростей двух пешеходов 5,75 км/ч. Скорость одного из них в 1,3 раза больше скорости другого. Найдите скорость каждого. )
— Решите оставшуюся часть задачи самостоятельно.
Проверка
Пусть скорость одного пешехода будет x.
Тогда скорость другого пешехода будет 1,3x.
Сумма скоростей двух пешеходов будет x + 1,3x.
А по условию задачи она составляет 5,75.
Значит, можем составить уравнение:
x + 1,3x = 5,75
2,3x = 5,75
x = 5,75 : 2,3
x = 2,5 (км/ч) — скорость одного пешехода.
2,5 ∙ 1,3 = 3,25 (км/ч) — скорость другого пешехода.
VI. Самостоятельная работа
Вариант 1
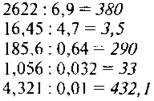
Вариант 2
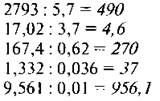
VII. Рефлексия
— Что нового узнали на уроке?
— Расскажите, как выполнить деление на 0,1; 0,01; 0,001.
Домашнее задание
С. 225, № 1491; с. 226, № 1492 (б).