ЛЕММА О РУКОПОЖАТИЯХ - РЕКОМЕНДАЦИИ ПО ОРГАНИЗАЦИИ ЗАНЯТИЙ С ИСПОЛЬЗОВАНИЕМ ДИДАКТИЧЕСКИХ МАТЕРИАЛОВ

Цель: научить учащихся применять лемму о рукопожатиях при решении задач.

Основное содержание

1. Изучаем лемму о рукопожатии.

2. Актуализируем метод от противного при решении задач.

Формы, методы и средства

Фронтальная работа, самостоятельная работа, соревнование в группах.

Проведение занятия

1. Знакомим учащихся с понятиями: “граф”, “вершины и ребра графа”, “степень вершины”.

2. Изучаем лемму о рукопожатиях и ее свойства. Проводим исторический экскурс названия леммы. Свое название лемма получила из-за следующей интерпретации: поскольку в каждом рукопожатии участвуют две руки, то при любом числе рукопожатий общее число пожатых рук (при этом каждая рука учитывается столько раз, во скольких рукопожатиях она участвовала) равно удвоенному числу рукопожатий.

3. Применяя лемму о рукопожатиях и метод от противного, решаем задания № 1—5 рубрики “Подумаем вместе”.

4. Используя подсказку, выполняем задание № 5 рубрики “Проверь себя”.

В помощь учителю

Ответы и решения к заданиям

“Подумаем вместе”

1. 10.

2. Соединить нельзя.

3. Нет.

4.

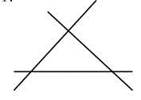
5. Нет.

“Проверь себя”

1. Нет.

2. Нельзя.

3. Нет.

4. Решение. (х ∙ 5 + у ∙ 6) : 2 < 32. Каждый пятиклассник имеет 11 друзей. Значит, в классе уже имеется 12 человек как минимум, а максимальное количество человек не превышает 32. Посчитаем пары “мальчик — девочка”:

5 ∙ м = 6 ∙ д

м = 5 ∙ к

= 6 ∙ к

Тогда м + д = 11 ∙ к. Значит, м + д — кратно 11. Число, которое кратно 11, больше 12 и меньше 32, — это число 22.

Ответ: 22.

5.

n = 4

n = 6

n = 8

n = 10

n = 12

Ответ: при всех четных n ≥ 4.

Оценка деятельности учащихся

Игра-соревнование. Учащиеся разбиваются на две команды и выполняют задания № 1—4 рубрики “Проверь себя”. Время — 15 минут. За каждый верный ответ — 1 балл. Победит та команда, которая наберет больше баллов.