Управление последовательностью выполнения - Язык Паскаль и начала программирования

2.3.1. Простая последовательность операторов

Все программы, которые мы писали до сих пор, выполнялись последовательно, оператор за оператором. Интересно, что тривиальная, в сущности, идея последовательного выполнения инструкций далеко не всем людям покоряется сразу и без боя; если вы не чувствуете себя уверенно, попробуйте написать что-нибудь вроде такого:

Поясним, что оператор readln работает примерно так же, как и уже знакомый нам read с тем отличием, что, прочитав всё, что требовалось, он обязательно дожидается окончания строки на вводе. Поскольку в нашем примере мы не указали параметров для этого оператора, он только это — ожидание окончания строки на вводе, то есть, попросту, ожидание нажатия клавиши Enter— и будет делать. Если нашу программу откомпилировать и запустить, она напечатает слово “First” и остановится в ожидании; пока вы не нажмёте Enter, больше ничего происходить не будет. В программе отработал её первый оператор и начал выполняться второй; он не завершится, пока на вводе не будет прочитан символ перевода строки.

Нажав Enter, вы увидите, что программа “ожила” и напечатала слово “Second”, после чего снова остановилась. Когда вы нажали Enter, первый из двух reading завершился, потом отработал второй writeln, который как раз и напечатал слово “Second”; после этого начал выполнение второй readln. Как и первый, он будет выполняться, пока вы не нажмёте Enter. Нажав Enter во второй раз, вы увидите, что программа напечатала “Third” и завершилась: это сначала завершился предпоследний оператор (readln), а затем отработал последний.

Во многих учебниках по информатике к программированию, особенно школьных, буквально все примеры программ заканчиваются этим вот readln’ом; временами readln в конце программы становится столь привычен, что и ученики, и даже некоторые учителя начинают воспринимать его “как мебель”, совершенно забывая, для чего он, в сущности, нужен в конце программы. Весь этот полушаманский кавардак начался с того, что в большинстве школ в качестве учебного пособия используются системы семейства Windows, а поскольку нормальную программу для Windowsнаписать очень сложно, программы пишутся “консольные”, а точнее — просто DOS’овские. Запускать программы ученикам, разумеется, предлагают исключительно из-под интегрированной среды типа Turbo Pascal или чем там кто богат, ну а озаботиться правильной настройкой этой среды при этом никто не считает нужным. В результате при запуске программы, созданной в интегрированной среде, операционная система открывает для выполнения такой программы окошко эмулятора MS-DOS, но это окошко автоматически исчезает, как только программа завершится; естественно, мы просто физически не успеваем прочитать, что наша программа напечатала.

Отметим, что эту “проблему” можно побороть самыми разными способами — настроить среду так, чтобы окно не закрывалось, или же просто запустить сеанс командной строки и выполнять откомпилированные программы из него; к сожалению, вместо этого учителя предпочитают показывать учениками, как вставлять в программы совершенно не относящийся к делу оператор, который в действительности нужен, чтобы окошко не закрывалось, пока пользователь не нажмёт Enter; впрочем, этого ученикам обычно не объясняют.

К счастью, мы с вами не используем ни Windows, ни интегрированные среды, так что подобные проблемы нас не касаются. Отметим заодно, что нелепый readln в конце каждой программы — далеко не единственная проблема, возникающая при использовании интегрированных сред. Например, привыкнув запускать программу на исполнение из-под интегрированной среды нажатием соответствующей клавиши, ученики упускают из виду понятие исполняемого файла, а вместе с ним компилятор и роль, которую он играет — многие вчерашние школьники уверены, что компиляция нужна, чтобы проверить программу на наличие ошибок, к больше, собственно говоря, низачем.

В качестве самостоятельного упражнения возьмите любой сборник англоязычных¹⁵ стихов и напишите программу, которая будет печатать какой-нибудь сонет строчка за строчкой, каждый раз дожидаясь нажатия Enter.

Последовательность выполнения операторов в программе часто изображают схематически в виде так называемых блок-схем. Блок-схема для простой последовательности операторов показана на рис. 2.1 (слева). Отметим, что обычные действия на блок-схемах традиционно изображают в виде прямоугольника, начало и конец рассматриваемого фрагмента программы обозначают маленьким кружком, а проверку условия — ромбиком; об этом — в следующем параграфе.

2.3.2. Конструкция ветвления

Единожды и навсегда заданная последовательность действий, какую мы использовали до сих пор, годится только для совсем тривиальных задач, которые к тому же приходится специально подбирать. В более сложных случаях последовательность приходится разветвлять на разные варианты, некоторые фрагменты программы повторять несколько (или даже очень много) раз подряд, временно перескакивать в другие места программы, с тем чтобы потом вернуться обратно, и так далее. Пожалуй, самая простая конструкция, нарушающая жесткую последовательность исполнения операторов — это так называемое ветвление; при его выполнении сначала проверяется некоторое условие, которое может оказаться истинным или ложным, причём во время написания программы мы не знаем, каким это условие окажется во время её исполнения (чаще всего бывает и так и так, причём за время одного исполнения программы). Ветвление может быть полным или неполным. При полном ветвлении (рис. 2.1, в центре) в программе указывается один оператор для выполнения при истинном условии и другой — для выполнения, если условие окажется ложным; при неполном ветвлении (рис. 2.1, справа) указывается всего один оператор, и его выполняют лишь в том случае, если условие оказалось истинным.

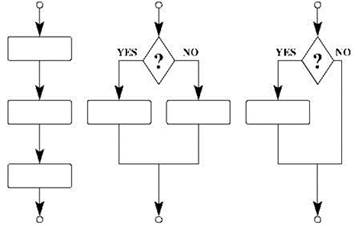
Рис. 2.1. Блок-схемы для простого следования, полного и неполного ветвления

В языке Паскаль простейшие случаи ветвления задаются с помощью оператора if, который несколько отличается от операторов, встречавшихся нам до сей поры. Дело в том, что этот оператор сложный: он содержит внутри себя другие операторы, в том числе, кстати, может содержать и другой оператор if. Начнём с простого примера: напишем программу, которая вычисляет модуль¹⁶введённого числа. Как известно, модуль равен самому числу, если число неотрицательное, а для отрицательных чисел модуль получается сменой знака. Для простоты картины будем работать с целыми числами. Программа будет выглядеть так:

Как видим, здесь сначала выполняется чтение числа; прочитанное число размещается в переменной х. Затем в случае, если введённое число строго больше нуля (выполняется условие х > 0), то печатается само это число, в противном же случае печатается значение выражения -х, то есть число, полученное из исходного сменой знака.

Примечательно здесь то, что конструкция

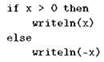
целиком представляет собой один оператор, но сложный, поскольку в нём содержатся операторы writeln(x) и writeln(-x).

Если говорить строже, то оператор if составляется следующим образом. Сначала пишется ключевое словоif, с помощью которого мы сообщаем компилятору, что сейчас в нашей программе будет конструкция ветвления. Затем записывается условие, представляющее собой так называемое логическое выражение; такие выражения подобны простым арифметическим выражениям, но результатом их вычисления является не число, а логическое значение (или значение типа boolean), то есть истина (true) или ложь (false). В нашем примере логическое выражение образовано операцией сравнения, которая обозначена знаком “>” (“больше”).

После условия необходимо написать ключевое слово then; по нему компилятор узнает, что наше логическое выражение кончилось. Далее идёт оператор, который мы хотим выполнять в случае, если условие выполнено; в нашем случае таким оператором выступает writeln(x). В принципе, условный оператор (то есть оператор if) на этом можно закончить, если нам нужно неполное ветвление; но если мы хотим сделать ветвление полным, мы пишем ключевое слово else, а после него — ещё один оператор, задающий действие, которое мы хотим выполнить, если условие оказалось ложно. Синтаксис оператора if можно выразить следующим образом:

Квадратными скобками здесь обозначена необязательная часть.

Отметим, что наше вычисление модуля можно написать и с неполным ветвлением, причём даже несколько короче:

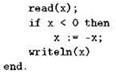
Здесь условие в операторе if мы изменили на “х строго меньше нуля” и в этом случае заносим в переменную х число, полученное из старого значения х заменой знака; если же х было неотрицательным, ничего не происходит. Затем, уже безотносительно того, ложным оказалось условие или истинным, выполняется оператор writeln, который печатает то, что в итоге оказалось в переменной х.

Обратите внимание на то, как в наших примерах расставлены отступы. Операторы, вложенные в if, то есть являющиеся его частью, сдвинуты вправо относительно того, во что они вложены, на уже знакомые нам четыре пробела; всего при избранном нами стиле получается восемь пробелов — два размера отступа¹⁷. Сами эти операторы в нашем примере оказываются на втором уровне вложенности.

Отметим ещё один важный момент. Начинающие очень часто делают достаточно характерную ошибку — ставят точку с запятой перед else; программа после этого не проходит компиляцию. Дело в том, что в Паскале точка с запятой, как уже говорилось, отделяет один оператор от другого; увидев точку с запятой, компилятор считает, что очередной оператор закончился, а в данном случае в качестве такового выступает if. Поскольку слово else не имеет смысла само по себе и может фигурировать в программе только как часть оператора if, а этот оператор с точки зрения компилятора уже закончился, встреченное затем слово else приводит к ошибке. Повторим ещё раз: перед else в составе оператора if точка с запятой не ставится!

2.3.3. Составной оператор

В предыдущем параграфе было сказано, что действия, выполняемые оператором if в случае истинного или ложного значения условия, задаются одним оператором (в примере предыдущего параграфа это были операторы writeln и присваивание). Но что делать, если требуется выполнить несколько действий?

Приведём классический пример такой ситуации. Допустим, у нас в программе есть переменные а и b какого-нибудь числового типа, и нам зачем-то очень нужно сделать так, чтобы значение в переменной а не превосходило значение в b, а если всё-таки превосходит, то значения надо поменять местами. Для временного хранения нам потребуется третья переменная (пусть она называется t); но чтобы поменять местами значения двух переменных через третью, там нужно сделать три присваивания, тогда как в теле if оператор предусмотрен только один.

Проблема решается с помощью так называемых операторных скобок, в роли которых в Паскале используются уже знакомые нам ключевые слова begin и end. Заключив произвольную последовательность операторов в эти “скобки”, мы превращаем всю эту последовательность вместе со скобками в один так называемый составной оператор. С учётом этого наша задача с упорядочением значений в переменных а и b решается следующим фрагментом кода:

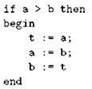
Подчеркнём ещё раз, что вся конструкция, состоящая из слов begin, end и всего, что между ними заключено, представляет собой один оператор — тоже, конечно, относящийся к “сложным”, поскольку включает в себя другие операторы.

Обратите внимание на оформление фрагментов кода, содержащих составной оператор! Существует три различных допустимых способа оформления конструкции, показанной выше; в нашем примере мы снесли begin на строчку, следующую за заголовком оператора if, но сдвигать его относительно if не стали; что касается end, его мы написали в той же колонке, где начинается конструкция, которую этот end закрывает.

Второй популярный способ оформления такой конструкции отличается тем, что begin оставляют на одной строке с заголовком if:

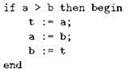
Обратите внимание, что end остался там же, где был! Можно считать, что он закрывает if; можно по-прежнему настаивать, что он закрывает begin, но горизонтальная позиция слова end в любом случае должна совпадать с позицией строки, где находится то (чем бы оно ни было), что закрывается данным end’ом. Иначе говоря, end должен быть снабжён в точности таким же отступом, каким снабжена строка, содержащая то, что этот end закрывает. Выполнение этого правила позволяет “схватить” общую структуру программы расфокусированным взглядом, а это при работе с исходным текстом очень важно.

Существует, хотя и гораздо реже используется, третий вариант оформления, при котором слово begin сдвигается на отдельный уровень вложенности, а то, что вложено в составной оператор, сдвигается ещё дальше. Выглядит это примерно так:

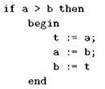
Рекомендовать использование такого стиля мы не будем в силу целого ряда причин, но в принципе он допустим.

2.3.4. Логические выражения и логический тип

Коль скоро мы начали пользоваться логическими (“булевскими”) выражениями, попробуем обсудить их более подробно. До сих пор в примерах мы рассматривали в качестве логических только операции “больше” и “меньше”, обозначаемые соответственно знаками “>” и “<”; кроме них Паскаль предусматривает операции “равно” (“=”), “не равно” (“<>”), “больше или равно” (“>=”), “меньше или равно” (“<=”) и некоторые другие, которые мы рассматривать не будем.

Логические выражения, как и арифметические, вычисляются: если, к примеру, у нас есть переменная х, имеющая тип integer, то выражения х + 1 и х > 1 различаются лишь типом значения: первое имеет тот же тип integer, тогда как второе — тип boolean; иначе говоря, если выражение х + 1 может дать в качестве результата произвольное целое число, то выражение х > 1 — только одно из двух значений, обозначаемых true и false, но это значение — результат сравнения — вычисляется, как и результат сложения.

Как мы уже упоминали, boolean может выступать в роли типа переменной, то есть мы можем описать переменную, хранящую логическое значение. Простое упоминание такой переменной само по себе представляет собой логическое выражение, и его можно использовать, например, в качестве условия в операторе if; переменным этого типа можно присваивать значения — разумеется, логические, то есть если слева от знака присваивания мы поставим переменную типа boolean, то справа нам придётся написать логическое выражение.

В частности, мы могли бы переписать пример с вычислением модуля, используя логическую переменную для хранения признака того, имеем ли мы дело с отрицательным числом. Выглядеть это будет так:

Здесь переменная negative, после присваивания будет содержать значение true, если введённое пользователем число (значение переменной х) оказалось меньше нуля, и false в противном случае. После этого мы используем переменную negative в качестве условия в операторе if.

Над логическими значениями язык Паскаль позволяет производить операции, соответствующие основным функциям алгебры логики (см. § 1.5.3). Эти операции обозначаются ключевыми словами not (отрицание), and (логическое “и”, конъюнкция), or (логическое “или”, дизъюнкция) и хоr (“исключающее или”). Например, с помощью оператора присваивания flag := not flag мы могли бы изменить значение логической переменной flag на противоположное; проверить, содержит ли целочисленная переменная к число, записываемое одной цифрой, можно с помощью логического выражения (k >= 0) and (k <= 9). Обратите внимание на скобки! Дело здесь в том, что в Паскале приоритет логических связок, в том числе операции and, выше, чем приоритет операций сравнения, подобно тому как приоритет умножения и деления выше, чем приоритет сложения и вычитания; если не поставить скобки, то выражение k >= 0 and k <= 9 компилятор Паскаля “разберёт” в соответствии с приоритетами так, как если бы мы написали k >= (0 and k) <= 9, что вызовет ошибку при компиляции.

Паскаль позволяет записывать сколь угодно сложные логические выражения; например, если переменная с имеет тип char, то выражение

позволит узнать, является ли её текущее значение латинской буквой. В принципе, здесь можно было бы обойтись без скобок вокруг and, поскольку приоритет and всё равно выше, чем or, но это тот случай, когда ликвидация избыточных скобок ничуть не добавит выражению ясности.

2.3.5. Понятие цикла; оператор while

Под циклом в программировании понимают некую последовательность действий, которая при работе программы выполняется (повторяется) сколько-то раз подряд. Сама такая последовательность действий, представленная одним или несколькими операторами, называется телом цикла, а каждое отдельное её выполнение называют итерацией; можно сказать, что выполнение всего цикла состоит из некоторого количества итераций. Тело цикла бывает коротким, а бывает и достаточно длинным, количество итераций может быть совсем небольшим (две, три, одна или даже ни одной), а может достигать многих миллиардов; ещё более интересен тот факт, что на момент начала выполнения цикла количество предстоящих итераций может быть заранее известно, а может определяться в ходе выполнения цикла. Встречаются даже такие циклы, которые выполняются “до бесконечности” — точнее, до тех пор, пока программу, выполняющую такой цикл, кто-нибудь не остановит.

Обычно в программе при выполнении цикла должно что-то изменяться от итерации к итерации, в противном случае цикл никогда не кончится; иногда, впрочем, такой бесконечный цикл организуется намеренно, но это скорее исключение. В простейшем случае между итерациями изменяется значение какой-нибудь переменной, а заданное для конкретного цикла логическое выражение, определяющее, продолжать цикл или прекратить, зависит от этой переменной.

В Паскале есть три разных оператора цикла; самым простым из них можно считать цикл while. В заголовке этого оператора указывается логическое выражение, которое будет вычисляться перед выполнением каждой итерации цикла; если результат вычисления окажется ложным, выполнение цикла будет немедленно завершено, если же получится “истина”, то будет выполнено тело цикла, заданное одним (возможно, составным) оператором. Начало конструкции отмечается ключевым словом while (англ. пока), тело отделяется от условия ключевым словом do. Синтаксис оператора while можно представить следующим образом:

Пусть нам, к примеру, нужно выдать на экран всё ту же надпись “Hello, world!”, но не один раз, а двадцать. Естественно, это можно и нужно сделать с помощью цикла, и цикл while для этой цели вполне подойдёт¹⁸, нужно только придумать, как задать условие цикла и как изменять что-то в состоянии программы таким образом, чтобы цикл выполнился ровно двадцать раз, а на двадцать первый условие оказалось ложным. Самый простой способ добиться этого — попросту считать, сколько раз цикл уже выполнился, и когда он выполнится двадцать раз, больше его не выполнять. Организовать такой подсчёт можно, введя целочисленную переменную для хранения числа, равного количеству итераций, которые уже отработали. Первоначально в эту переменную мы занесём ноль, а в конце каждой итерации будем увеличивать её на единицу; в результате в каждый момент времени эта переменная будет равна количеству выполненных к настоящему моменту итераций. Такую переменную часто называют счётчиком цикла.

Кроме увеличения переменной на единицу, в теле цикла нужно сделать ещё одно действие — собственно то, ради чего всё и затевалось, то есть печать строки. Получается, что операторов в теле цикла нам нужно два, а синтаксис оператора while предусматривает в качестве тела цикла только один оператор; но мы уже знаем, что это не проблема — достаточно объединить все операторы, которые нам нужны, в один составной оператор с помощью операторных скобок begin и end. Целиком наша программа будет выглядеть так:

Обратите внимание на то, что в теле цикла мы сначала расположили оператор печати, и лишь потом — оператор присваивания, увеличивающий переменную i на единицу. Для данной конкретной задачи ничего бы не изменилось, если бы мы поменяли их местами; но делать так всё же не следует. Как показывает практика, лучше — безопаснее в плане возможных ошибок — всегда следовать одному достаточно простому соглашению: подготовка значений переменных для первой итерации цикла while должна происходить непосредственно перед циклом, а подготовка значений для следующей итерации должна располагаться в самом конце тела цикла. В данном случае подготовка к первой итерации состоит в присваивании нуля счётчику цикла, а подготовка к следующей — в увеличении счётчика на единицу; оператор i := 0 мы поставили перед самым while, а оператор i := i + 1 — последним в его теле.

Можно подойти к этому вопросу по-другому. Коль скоро переменная i хранит число напечатанных к данному моменту строчек (сначала ноль, потом каждый раз на единицу больше), то вполне логично сначала напечатать очередную строку, и лишь потом учесть этот факт, увеличив переменную на единицу.

Значение счётчика цикла можно использовать не только в условии, как мы это сделали в программе hello20, но и, при необходимости, в теле цикла. Допустим, нас заинтересовали квадраты целых чисел от 1 до 100; напечатать их можно, например, так:

Пользоваться результатом этой программы будет не очень удобно, поскольку она каждое число расположит на отдельной строке. Мы можем усовершенствовать её, заменив writeln на write; но если так поступить, не предприняв никаких дополнительных мер, то есть просто убрать буквы ln ив таком виде запустить программу, результат нас может совершенно обескуражить:

Дело в том, что оператор write исполняет нашу волю буквально: если мы потребовали напечатать число, то он выдаст на печать цифры, составляющие десятичную запись этого числа, к больше ничего — ни пробелов, ни каких-либо других разделителей. Внимательно посмотрев на вывод, мы можем заметить, что цифры, составляющие запись чисел 1, 4, 9, 16 и т. д., никуда не делись, просто числа ничем не отделены одно от другого.

Решить эту проблему очень просто, достаточно сказать оператору write, что мы желаем, чтобы он после каждого числа выводил ещё и символ пробела. Кроме того, в конце программы, то есть уже после цикла, желательно добавить оператор writeln, чтобы программа, прежде чем завершиться, перевела строку на печати, и приглашение командной строки после её завершения появилось бы на новой строке, а не сливалось с напечатанными числами. Целиком программа будет выглядеть так:

Рассмотрим теперь пример такого цикла, для которого мы заранее не знаем количество итераций. Допустим, мы пишем некую программу, которая в какой-то момент должна спросить у пользователя его год рождения, и нам при этом нужно проверить, действительно ли введённое число может представлять собой год рождения. На момент написания этой книги (2016 год) на Земле оставалось всего два человека, про которых достоверно известно, что они родились раньше 1900 года; будем считать, что год рождения пользователя заведомо не может быть меньше, чем 1900. По аналогичным причинам будем считать, что год рождения пользователя не может превышать 2013, поскольку трёхлетние дети не умеют пользоваться компьютером; если к тому времени, когда вы эту книгу читаете, прошло достаточно времени, вы можете самостоятельно скорректировать эти значения.

Так или иначе, нам нужно попросить пользователя ввести его год рождения; если ввод нас не устраивает, необходимо сказать пользователю, что он, по-видимому, ошибся, и попросить повторить ввод. В секции описаний мы можем предусмотреть переменную year:

Что касается самого диалога с пользователем, то реализовать его можно так:

С такой программой может состояться, например, следующий диалог:

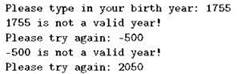
Заметим, что здесь цикл может не выполниться ни одного раза — если пользователь сразу же введёт нормальный год; с другой стороны, пользователь может попасться упрямый, так что мы в действительности не можем знать, каково максимальное число итераций нашего цикла. Можно предположить, что, скажем, на миллиард итераций терпения пользователя всё же не хватит, но какое конкретно число указать в качестве верхней границы? Сто? Тысячу? Предположение, что на 1000 итераций пользователя хватить ещё может, а на 1001 — уже нет, выглядит достаточно нелепо, и точно так же нелепо будет выглядеть в этой роли любое другое конкретное число; проще вообще не строить на этот счёт никаких предположений.

2.3.6. Цикл с постусловием; оператор repeat

В операторе while, которому был посвящён предыдущий параграф, сначала проверяется условие, и только после этого, возможно, выполняется первая итерация. Такие конструкции в программировании называются циклами с предусловием.

Кроме них, при написании программ иногда используются циклы с постусловием, в которых сначала выполняется тело цикла, и только после этого проверяется, следует ли выполнять его снова; таким образом, в циклах с постусловием тело выполняется по меньшей мере один раз. Язык Паскаль предусматривает для циклов с постусловием специальный оператор, который задаётся ключевыми словами repeat и until; операторы, составляющие тело цикла, записывается между этими словами, причём таких операторов может быть сколько угодно, применение операторных скобок здесь не требуется; после слова until записывается условие выхода из цикла — логическое выражение, ложное значение которого указывает на необходимость продолжать цикл, а истинное — на то, что цикл пора прекращать. Блок-схемы циклов с предусловием и постусловием показаны на рис. 2.2.

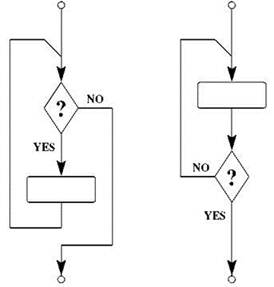
Рис. 2.2. Блок-схемы циклов с предусловием и постусловием

Например, если бы нам по каким-то причинам не требовалось, как в примере на стр. 231, выстраивать диалог с пользователем, а просто было бы нужно вводить с клавиатуры целые числа, пока очередное из них не попадёт в отрезок от 1900 до 201S, мы могли бы сделать это так:

Рассмотрим другой пример. Следующий цикл вводит числа с клавиатуры и складывает их, пока общая сумма не окажется больше 1000:

Синтаксис оператора repeat можно представить следующим образом:

repeat <операторы> until <условие>

Обычно в программах оператор repeat встречается гораздо реже, чем while, но знать о его существовании в любом случае необходимо.

2.3.7. Арифметические циклы и оператор for

Вернёмся к примерам, приведённым в начале § 2.3.5; напомним, там мы писали циклы, чтобы выдать одну и ту же надпись двадцать раз и чтобы напечатать квадраты всех целых чисел от одного до ста. Циклы, которые мы написали для решения этих простых задач, обладают одним очень важным свойством: на момент входа в цикл точно известно, сколько раз он будет выполняться, и нужное количество итераций обеспечивается путём их подсчёта в целочисленной переменной. Такие циклы называют арифметическими.

Арифметические циклы встречаются настолько часто, что во многих языках программирования, включая Паскаль, для них предусмотрен специальный оператор; в Паскале такой оператор называется for. Как это часто бывает, рассказать о нём будет проще, если сначала привести пример, а потом дать пояснения, поэтому мы начнём с того, что перепишем программы hello20 и square100, используя оператор арифметического цикла. Начнём с первой:

Конструкция for i := 1 to 20 do означает, что в качестве переменной цикла будет использоваться переменная i, её начальное значение будет 1, финальное значение — 20, то есть она должна пробежать все значения от 1 до 20, и для каждого такого значения будет выполнено тело цикла. Поскольку таких значений 20, тело будет выполнено двадцать раз, что нам и требуется. Если сравнить получившуюся программу с той, что мы писали ранее, можно заметить, что её текст получился гораздо компактнее; более того, для человека, который уже привык к синтаксису for, такой вариант существенно проще понять.

Перепишем теперь программу square100, взяв за основу вариант, печатающий числа через пробел. С использованием цикла for того же самого эффекта можно достичь так:

Как видим, в теле цикла for можно использовать значение переменной цикла. Отметим сразу же, что к этому значению можно обращаться, а вот менять его ни в коем случае нельзя. Менять переменную цикла во время выполнения цикла — это прерогатива самого оператора for, попытки вмешаться в его работу могут привести к непредсказуемым последствиям. Кроме того, с переменной цикла связано ещё одно ограничение: после завершения цикла for значение переменной цикла считается неопределённым, то есть мы не должны предполагать, что эта переменная будет равна какому-то конкретному числу. Конечно, какое-то значение там будет, но оно может зависеть от версии компилятора и даже от того, в каком месте в программе встретился цикл. Попросту говоря, создатели компилятора не обращают никакого внимания на то, какое значение оставить в переменной цикла после его завершения, и могут оставить там всё что угодно.

В обоих наших примерах переменная цикла изменялась в сторону увеличения, но можно заставить её пробегать значения в обратном направлении, от большего к меньшему. Для этого слово toзаменяют словом downto. Например, программа

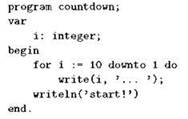
напечатает строку

Формально синтаксис оператора for можно представить следующим образом:

for <перем> : = <нач> to|downto <кон> do <оператор>

Здесь <перем> — это имя целочисленной переменной, <нач> — начальное значение, <кон> — конечное значение. Оба этих значения могут задаваться не только явным образом написанными числами, как в наших примерах, но и произвольными выражениями, лишь бы результатом этих выражений было целое число. Выражения будут вычислены один раз перед началом выполнения цикла, так что, если в них входят переменные и значения этих переменных изменятся во время выполнения цикла, то на работу самого цикла это уже никак не повлияет.

Если после вычисления начального и конечного значений оказалось, что конечное значение меньше (а для downto — наоборот, больше) начального, то это само по себе не ошибка: цикл не выполнится ни одного раза, и в некоторых случаях это свойство можно использовать.

На самом деле переменная цикла, используемая в операторе for, может быть не только целочисленной; несколько позже мы введём понятие порядкового типа, которое объединит все целочисленные типы, а также диапазоны, символьный тип, перечислимые типы к логический тип; оператор for можно использовать с любым таким типом. Конечно, тип выражений, задающих начальное и конечное значение, обязан совпадать с типом переменной цикла.

2.3.8. Вложенные циклы

Рассмотрим следующую задачу. Нужно напечатать “наклонную черту” размером во весь экран, состоящую из символов “*”. Результат должен выглядеть примерно так:

(для экономии места мы показали всего восемь строк, хотя их должно быть 24). Сделать это, в принципе, очень просто: нужно вывести 24 строки, причём в каждой строке сначала напечатать некоторое количество пробелов, а потом выдать “звёздочку” и перевести строку. В самой первой строке мы вообще не печатаем пробелов, сразу выдаём звёздочку; можно считать, что мы печатаем ноль пробелов. В каждой последующей строке печатается на один пробел больше, чем в предыдущей. Если считать, что номера строк у нас идут от 1 до 24, то нетрудно заметить, что в строке с номером п должно быть n — 1 пробелов.

Ясно, что выводить строки нужно циклом, по одной итерации на строку. Поскольку на момент входа в цикл мы точно знаем, сколько будет итераций, применить следует цикл for. Переменную цикла назовём n, её значение будет соответствовать номеру строки. Цикл должен выглядеть примерно так¹⁹:

Осталось понять, как организовать печать нужного количества пробелов. Сколько их печатать, мы уже знаем: n - 1. Иными словами, загадочное “{ напечатать нужное количество пробелов }” в нашем коде нужно заменить на что-то такое, что напечатает нам n - 1 пробел. Как несложно догадаться, для этого тоже нужен цикл, и тоже арифметический: мы ведь знаем на момент его начала, сколько должно быть итераций. Так мы приходим к концепции вложенных циклов.

Ясно, что во вложенном цикле нужно задействовать другую переменную цикла, чтобы циклы не конфликтовали; в конце концов, пока внешний цикл не завершился, никто не вправе менять его переменную, в том числе не вправе это делать и внутренний цикл. Описав для внутреннего цикла переменную m, мы получим следующую программу:

Рассмотрим задачу чуть более сложную — вывести на экран фигуру примерно такого вида:

Эту фигуру часто называют “алмазом” (англ. diamond). Высоту фигуры мы в этот раз прочитаем с клавиатуры, то есть попросим пользователя сказать нам, какой высоты “алмаз” он хочет увидеть. Дальнейшее потребует некоторого анализа.

Прежде всего заметим, что высота нашей фигуры есть всегда число нечётное, так что, если пользователь введёт чётное число, то придётся попросить его повторить ввод; то же самое, по-видимому, следует сделать, если введённое число окажется отрицательным. Нечётное число, как известно, представляется в виде 2n + 1, где n — целое; верхняя часть нашей фигуры будет состоять из n + 1 строк. Для фигуры, показанной выше, высота составляет семь строк, а n будет равно трём.

Теперь нам нужно понять, сколько пробелов и где нужно напечатать, чтобы получить искомую фигуру. Заметим для начала, что при печати самой первой строки нам придётся выдать п пробелов, при печати второй строки — n — 1 пробел, и так далее; при печати последней, (n + 1)’й строки пробелов не нужно вовсе (можно считать, что мы их печатаем ноль штук).

Чуть сложнее обстоят дела с пробелами после первой звёздочки. В первой строке вообще ничего такого не нужно, там всего одна звёздочка; а вот дальше происходит довольно интересный процесс: во второй строке нужно напечатать один пробел (и после него вторую звёздочку), в третьей строке — уже три пробела, в четвёртой — пять, и так далее, каждый раз на два пробела больше. Несложно догадаться, что для строки с номером k (k > 1) нужное количество пробелов выражается формулой 1 + 2(k — 2) = 2k — 3. Интересно, что с некоторой натяжкой можно считать эту формулу “верной” также и для случая k =1, где она даёт —1: если операцию “напечатать m пробелов” доопределить на отрицательные т как “возврат назад на соответствующее число знакомест”, получится, что, напечатав первую звёздочку, мы должны будем вернуться обратно на одну позицию и вторую звёздочку напечатать точно поверх первой. Впрочем, так сделать гораздо труднее, чем просто проверить значение к, и если оно равно единице, то после первой звёздочки не печатать больше ни пробелов, ни звёздочек, а сразу перевести строку.

Полностью печать строки с номером k должна выглядеть так: сначала мы печатаем n +1 — k пробелов, затем звёздочку; после этого если k равно единице, просто выдаём перевод строки и считаем печать строки оконченной; в противном случае печатаем 2k — 3 пробела, звёздочку и только после этого делаем перевод строки. Всё это нам надо проделать для k от 1 до n +1, где n— “полувысота” нашего “алмаза”.

После того, как верхняя часть фигуры будет напечатана, нам нужно будет как-то выдать ещё её нижнюю часть. Мы могли бы продолжить нумерацию строк и вывести формулы для количества пробелов в каждой строке с номером n + 1 < k ≤ 2n + 1, что, в принципе, не так уж сложно; однако можно поступить ещё проще, заметив, что печатаемые теперь строки в точности такие же, как и в верхней части фигуры, то есть мы сначала печатаем такую же строку, как n-я, потом такую же, как (n — 1)-я, и так далее. Самый простой способ — для каждой строки исполнить ровно такую процедуру печати, как описано параграфом выше, только в этот раз номера строк k у нас пробегут в обратном направлении все числа от n до 1.

Наша программа будет состоять из трёх основных частей: ввод числа, означающего высоту фигуры, печать верхней части фигуры, печать нижней части. Вот её текст (напомним, что слова div и mod означают деление с остатком и остаток от деления):

Легко заметить очень серьёзный недостаток нашей программы: циклы для рисования верхней и нижней частей фигуры различаются только заголовком, а тела в них абсолютно одинаковые. Вообще-то программисты считают, что так делать нельзя: если у нас в программе содержатся две или больше копий одного и того же кода, то, если вдруг мы захотим исправить один из этих фрагментов (например, найдя в нём ошибку), скорее всего их придётся править все, а это ведёт к непроизводительным трудозатратам (что ещё полбеды) и провоцирует ошибки из-за того, что мы часть отредактировали, а часть забыли. Но справиться с этой проблемой мы сможем, только изучив так называемые подпрограммы, которым будет посвящена следующая глава.