Программы и данные - Предварительные сведения

1.6.1. Об измерении количества информации

Как мы уже знаем, при использовании компьютера для хранения и обработки информации используется двоичное представление; иначе говоря, любая информация в компьютере представляется нулями и единицами. Говорят, что наименьшей единицей информации в компьютерной обработке является бит; само слово бит(bit) образовано от английских Binary digiT, то есть “двоичная цифра”.

Хотя компьютеры весьма удобны для обработки информации, всё-таки информация как таковая существует сама по себе и существовала задолго до появления первых счётных машин. Будучи явлением вполне объективным, информация поддаётся измерению, и под этим углом зрения столь привычный нам бит совершенно неожиданно предстаёт в новом свете. Получить информацию — значит уменьшить неопределённость; в таком случае бит — это количество информации, которое уменьшает неопределённость вдвое. Проиллюстрировать сказанное нам позволит следующая задача:

Вася задумал натуральное число, не превосходящее 1000, и предложил Пете угадать его, пообещав, что будет честно отвечать на вопросы, но только такие, которые предполагают ответ “да” или “нет”. За какое количество вопросов Петя может гарантированно узнать, какое число задумано?

Очевидно, что каждый ответ Васи даёт Пете ровно один бит информации. Начальная неопределённость составляет 1000 вариантов. Если каждый полученный бит информации будет снижать неопределённость вдвое, то после получения 10 бит неопределённость понизится в 2¹⁰ = 1024 раза, то есть окажется меньше единицы, так что за десять вопросов число должно быть гарантированно узнано. Осталось понять, как правильно сформулировать вопросы.

Если подходить к задаче с абстрактной точки зрения, достаточно перед заданием очередного вопроса каким-то (произвольным) образом разбивать все оставшиеся варианты на два равных по мощности множества, ну или, по крайней мере, отличающихся друг от друга по мощности не более чем на единицу, и спрашивать Васю, находится ли задуманное им число в одном из двух множеств. Например, Петя мог бы взять тысячу карточек, написать на каждой из них число, поделить карточки случайным образом на две колоды по 500 карточек в каждой, вручить одну колоду Васе и спросить, написано ли задуманное им число на одной из карточек; в случае отрицательного ответа выбросить все карточки, которые были вручены Васе, в случае же ответа положительного — наоборот, выбросить все, которые Васе не давались. Оставшиеся 500 карточек поделить на две колоды по 250 и одну из них снова предложить Васе. После второго ответа будет выброшено ещё 250 карточек, оставшиеся будут поделены на две колоды по 125. После третьего ответа оставшееся число карточек окажется нечётным, так что придётся поделить их на неравные части, и в результате после четвёртого ответа у нас, в зависимости от везения, останется то ли 64, то ли 63 карточки; после пятого ответа — то ли 31, то ли 32; после шестого — то ли 15, то ли 16; после седьмого — семь или восемь, после восьмого — три или четыре, после девятого — одна или две. Если осталась одна карточка, то задача решена, если же осталось две — придётся задать десятый вопрос, уж после него у нас гарантированно больше одной карточки остаться не может.

Конечно, технически вся эта канитель с карточками довольно занудна, хотя с математической точки зрения процесс построен безупречно. Но никто ведь не заставляет разбивать варианты на два множества как попало; за счёт небольшой технической поправки Петя вполне может обойтись без рисования карточек, а Васе не придётся их раз за разом просматривать. Достаточно поделить варианты пополам так, чтобы все числа из одного множества были меньше любого из чисел другого множества. На первом шаге Петя может спросить Васю, находится ли задуманное число в диапазоне от 1 до 500. В зависимости от ответа у Пети останутся в рассмотрении числа либо от 1 до 500, либо от 501 до 1000; следующий вопрос будет, соответственно, находится ли задуманное в диапазоне [1, 250] или [501, 750], и так далее; на каждом шаге количество вариантов, оставшихся в рассмотрении, будет уменьшаться вдвое.

Количество информации не обязано измеряться целым количеством битов. Широко известен, например, простенький карточный фокус, в котором ведущий сначала раскладывает на столе неполную колоду карт и предлагает зрителю загадать какую-нибудь карту. Затем ведущий раскладывает карты в три ряда и спрашивает, в каком из рядов находится карта; получив ответ, он собирает карты и снова раскладывает их в три ряда, а затем ещё раз. Получив третий ответ, ведущий откуда-то из середины названного ряда вытаскивает именно ту карту, которую загадал зритель, либо, для пущего эффекта, снова собирает карты в колоду, сколько-то там карт отсчитывает и сбрасывает, а оказавшуюся сверху карту открывает, и это оказывается именно та карта, которая была загадана.

В этом фокусе используется 27 карт, именно поэтому колода нужна неполная; обычно ведущий заранее откладывает в сторону шестёрки, семёрки и одну восьмёрку. Разложив карты в три ряда по девять и узнав от зрителя, в каком из рядов находится нужная карта, ведущий собирает карты, но не смешивает их; карты из ряда, названного зрителем, ведущий кладёт в середину колоды, поместив остальные два ряда сверху и снизу. Затем он раскладывает карты по одной снова в три ряда по девять; нетрудно догадаться, что “нужные” карты оказываются в каждом из новых рядов тремя средними, а остальные (три с любого края в любом ряду), хотя и выложены на стол, но пришли из рядов, которые заведомо не участвуют в рассмотрении. Повторив свой вопрос и снова поместив нужный ряд между двумя другими, ведущий снова раскладывает их по одной, но в этот раз в рассмотрении участвуют на самом деле только те три карты, которые лежат в самой середине каждого ряда; остальные лишь создают “массовку”. Получив ответ, в каком ряду загаданная карта в этот раз, ведущий теперь уже точно знает, какая карта была загадана — она ведь находится в середине. Её можно просто достать, но тогда зритель может сразу догадаться, что происходит; поэтому обычно карты снова складывают в колоду, причём “нужный” ряд опять кладут посередине, отсчитывают 13 карт сверху и открывают следующую, четырнадцатую, которая как раз и лежала в середине нужного ряда и, следовательно, именно её загадал зритель.

В нашем разговоре о количестве информации этот простой фокус примечателен лишь тем, что с каждым ответом зрителя неопределённость, исходно составлявшая 27 вариантов, уменьшается втрое; такую единицу информации иногда называют тритом. Если попытаться выразить трит в битах, получится иррациональное число log2 3: в самом деле, сколько раз нужно уменьшать неопределённость вдвое (то есть получать один бит информации), чтобы в итоге она уменьшилась втрое? Естественно, именно такое число раз, которое, если в такую степень возвести двойку, даст тройку, а это и есть пресловутый логарифм.

Рассмотрим более сложный случай.

Два археолога, изучая архив старого замка, узнали, что во дворе замка, имеющем форму прямоугольника 60 х 80 метров, закопан клад. Пока один археолог ездил за металлоискателем, второй археолог продолжил изучение архивов и выяснил, что клад закопан в юго-восточной части двора, причём на расстоянии не более 30 м. от короткой стены замка и не более 20 м. от длинной. Какова информационная ценность его открытия?

Почему-то эта задача ставит в тупик даже многих программистов; между тем нетрудно убедиться, что исходная площадь поиска клада составляла 60 х 80 м², тогда как после обнаружения новых сведений она сократилась до 30 х 20 м², то есть ровно в восемь раз. Это и есть уменьшение неопределённости; коль скоро один бит уменьшает неопределённость вдвое, то здесь мы имеем дело с тремя битами информации.

Как правило, в задачах, подобных этой, речь идёт о вероятностях наступления неких событий, а затем о том, что было получено сообщение, указывающее на наступление некоторой комбинации таких событий, к спрашивается, какова информационная ёмкость полученного сообщения. Например:

В первый день турнира по настольному теннису Васе предстояло сыграть сначала с Петей, а затем с Колей. Наблюдая тренировочные игры, проходившие до турнира, болельщики оценили, что Вася играет с Колей приблизительно на равных, а вот Петя побеждает Васю в 75% случаев.

Маша не смогла присутствовать на турнире, но болела за Васю к попросила друзей сообщить ей результаты обеих его игр. Через некоторое время ей пришло SMS-сообщение, в котором говорилось, что Вася обыграл обоих соперников. (1) Какова информационная ёмкость этого сообщения? (2) Если бы Вася, наоборот, проиграл обе партии и Маше сообщили бы об этом, какова тогда была бы ёмкость сообщения?

Решаются такие задачи ничуть не сложнее задачи про археологов во дворе замка, просто вместо двора замка здесь мы имеем пространство элементарных исходов, а вместо площади — вероятность. Вероятность победы Васи в первой партии, согласно условиям задачи, составляет 1/4, вероятность победы во второй партии — 1/2; поскольку для комбинаций независимых событий вероятности перемножаются, получается, что вероятность того, что Вася выиграет обе партии, составляет то есть информация о том, что Вася выиграл обе партии, уменьшает неопределённость в восемь раз. Следовательно, информационная ценность сообщения составляет 3 бита.

Вероятность того, что Вася проиграет обе партии, составляет 3/8, так что здесь информационная ценность сообщения окажется, во-первых, ниже, поскольку наступило более вероятное событие, и, во-вторых, в этот раз искомое число будет не только не целым, но даже и не рациональным: поскольку неопределённость в этот раз уменьшается в 8/3 раза, информационный объём сообщения составит

Наряду с термином “бит” используется также термин “байт” (англ. byte), обычно подразумевающий восемь бит. Как ни странно, это не всегда так: существовали компьютеры, у которых минимальная ячейка памяти составляла, например, семь бит, а не восемь, и на этих компьютерах байтом называли обычно как раз количество информации, хранящееся в одной такой ячейке; ввели даже специальный термин октет для обозначения именно восьми бит. К счастью, вам вряд ли придётся на практике столкнуться с пониманием байта, отличным от восьми бит, но иметь в виду историю возникновения этого термина в любом случае стоит.

Восьмибитный байт может принимать одно из 256 возможных значений; обычно эти значения интерпретируют либо как число от 0 до 255, либо как число от -128 до 127. Восьмибитные ячейки памяти хорошо подходят для хранения букв, составляющих текст, если этот текст написан на языке, использующем алфавит вроде латиницы; для представления каждой отдельной буквы при этом используется так называемый код символа, причём всех различных кодов существенно меньше, чем существует возможных значений байта. С многоязычными текстами всё несколько хуже: для кириллицы кодов ещё хватает, а, например, с иероглифами этот подход уже не годится. К вопросу о кодировке текста мы ещё вернёмся.

Раз уж речь зашла о ячейках памяти, следует заметить, что в них приходится хранить вообще любую информацию, которая обрабатывается компьютером, в том числе программы или, точнее, коды команд, из которых программы состоят. Когда диапазона значений одной ячейки не хватает, используют несколько ячеек, находящихся в памяти подряд, и говорят уже не о ячейке, а об области памяти.

Важно понимать, что сама по себе ячейка памяти “не знает”, как именно следует интерпретировать хранящуюся в ней информацию. Рассмотрим это на простейшем примере. Пусть у нас есть четыре идущие подряд ячейки памяти, содержимое которых соответствует шестнадцатеричным числам 41, 4Е, 4Е и 41 (соответствующие десятичные числа — 65, 78, 78, 65). Информацию, содержащуюся в такой области памяти, можно с совершенно одинаковым успехом истолковать как целое число 1095650881; как дробное число (т. н. число с плавающей точкой) 12.894105; как текстовую строку, содержащую имя ’ANNA’; наконец, как последовательность машинных команд. В частности, на процессорах платформы i386 это будут команды, условно обозначаемые inc есх, dec esi, dec esi, inc есх; О том, что эти команды делают, мы расскажем во втором томе книги.

1.6.2. Машинное представление целых чисел

О том, что компьютеры используют двоичную систему счисления, мы уже говорили. При этом компьютеры, будучи реально существующими техническими устройствами, накладывают некоторые ограничения на представление целых чисел. В математике множество целых чисел бесконечно, то есть каково бы ни было число N, всегда существует следующее число N + 1. Для этого и количество знаков в записи числа, какую бы систему мы ни использовали, не должно никак ограничиваться — но вот как раз это требование исполнить технически невозможно (даже чисто теоретически: ведь количество атомов во вселенной считается конечным).

На практике для компьютерного представления целого числа выделяется некоторое фиксированное количество разрядов (бит); обычно это 8 бит (одна ячейка), 16 бит (две ячейки), 32 бита (четыре ячейки) или 64 бита (восемь ячеек). Ограничение разрядности приводит к появлению “наибольшего числа”, и это касается не только двоичной системы. Представьте себе, например, простое счётное устройство, используемое в электрических счётчиках и механических одометрах старых автомобилей: цепочку роликов, на которых нанесены цифры и которые могут прокручиваться, а проходя через “точку переноса” (с девятки на ноль), прокручивают на единицу следующий ролик. Допустим, такое устройство состоит из пяти роликов (см. рис. 1.12). Сначала мы видим на нём число “ноль”: 00000. По мере прокручивания правого ролика число будет меняться, мы увидим 00001, потом 00002 и так до 00009. Если теперь провернуть самый правый ролик ещё на единичку, мы снова увидим в правой позиции ноль, но при этом самый правый ролик зацепит своего соседа слева и заставит его провернуться на единичку, так что мы увидим 00010, то есть число “десять”; мы наблюдали при этом хорошо известный с младших классов перенос: “девять плюс один, ноль пишем, один в уме”. То же самое произойдёт при переходе от числа 00019 к числу 00020 и так далее, а когда мы увидим число 00099 и прокрутим правый ролик ещё на единичку, в зацепление попадут сразу два его соседа, так что на единицу вперёд прокрутятся сразу три ролика, и мы получим число “сто”: 00100.

Рис. 1.12. Механический счётчик

Теперь уже легко понять, откуда берётся такой монстр, как “наибольшее возможное число”: рано или поздно наш счётчик досчитает до 99999, и теперь увеличивать число окажется некуда; когда мы в очередной раз прокрутим правый ролик на единицу вперёд, он зацепит за собой все остальные ролики, они все перейдут на следующую цифру, и мы снова увидим одни нули. Если бы у нас слева был ещё один ролик, он бы зацепился и показал единичку, так что результат бы был 100000 (что совершенно правильно), но у нас всего пять роликов, шестого нет. Такая ситуация называется перенос в несуществующий разряд; мы уже сталкивались с ней при обсуждении вычитания на арифмометре Паскаля. Ясно, что такая ситуация не может возникнуть, когда мы пишем числа на бумаге: всегда можно дописать ещё одну цифру слева; когда же число представлено состоянием некой группы технических устройств, будь то цепочка роликов или набор триггеров в оперативной памяти компьютера, возможности приделать к числу ещё одну цифру у нас нет.

При использовании двоичной системы счисления происходит примерно то же самое с той разницей, что используется всего две цифры. Допустим, мы используем для подсчёта каких-нибудь предметов или событий ячейку памяти, которая содержит восемь разрядов. Сначала в ячейке ноль: 00000000. Добавив единицу, получаем двоичное представление единицы: 00000001. Добавляем ещё одну единицу, младший (самый правый) разряд увеличивать некуда, поскольку у нас только две цифры, поэтому он снова становится нулевым, но при этом происходит перенос, в результате которого единица появляется во втором разряде: 00000010; это двоичное представление числа 2. Дальше будет 00000011, 00000100 и так далее. В какой-то момент во всех имеющихся разрядах окажутся единицы, так что прибавлять дальше будет некуда: 11111111; это двоичное представление числа 255 (2⁸ — 1). Если теперь прибавить ещё единицу, вместо числа 256 мы получим “все нули”, то есть просто ноль; произошел уже знакомый нам перенос в несуществующий разряд. Вообще при использовании для представления целых положительных чисел позиционной несмешанной системы счисления по основанию N и ограничении количества разрядов числом к максимальное число, которое мы можем представить, составляет N^k — 1; так, в нашем примере со счётчиком было пять разрядов десятичной системы, и максимальным числом оказалось 99999 = 10⁵ — 1, а в примере с восьмибитной ячейкой система использовалась двоичная, разрядов было восемь, так что максимальным числом оказалось 2⁸ — 1 = 255.

Некоторые языки программирования высокого уровня позволяют оперировать сколь угодно большими целыми числами, лишь бы хватило памяти, но мы пока не будем рассматривать такие инструменты: нам важно понять, как работает компьютер, тогда как языки высокого уровня от нас устройство компьютера стараются по возможности скрыть.

Мы уже отмечали, что одна ячейка обычно состоит из восьми разрядов и может, соответственно, хранить число от 0 до 255, если же требуется хранить число из большего диапазона, используют несколько идущих подряд ячеек памяти, и здесь совершенно неожиданно возникает вопрос, в каком порядке располагать части представления одного числа в соседних ячейках памяти. На разных машинах используют два разных подхода к порядку следования байтов. Один подход, называемый little-endian⁴⁸, предполагает, что первым идёт самый младший байт числа, далее в порядке возрастания, и самый старший байт идёт последним. Второй подход, который называют big-endian, прямо противоположен: сначала идёт старший байт числа, а младший располагается в памяти последним.

Например, число 7500 в шестнадцатеричной системе записывается как 1D4C₁₆. Если представить его в виде 32-битного (4-байтного) целого на компьютере, использующем подход big-endian, то область памяти длиной в четыре ячейки, хранящая это число, окажется заполнена так: первые два байта (с наименьшими адресами) получат значение 00, следующий (третий) будет установлен в значение 1D, и последний, четвёртый — в значение 4С: 00 00 1D4C. Если то же самое число записать в память компьютера, использующего подход little-endian, то значения отдельных байтов в соответствующей области памяти окажутся идущими в противоположном порядке: 4С 1D 00 00.

Большинство компьютеров, используемых в наши дни, относятся к категории “little-endian”, то есть хранят младший байт первым, хотя машины “big-endian” тоже иногда встречаются.

Посмотрим теперь, как быть, если необходимо работать не только с положительными числами. Ясно, что нужен какой-то другой способ интерпретации комбинаций двоичных разрядов, такой, чтобы какие-то из комбинаций считались представляющими отрицательное число. Будем в таких случаях говорить, что ячейка или область памяти хранит знаковое целое число, в отличие от предыдущего случая, когда говорят о беззнаковом целом числе.

На заре вычислительной техники для представления отрицательных целых чисел пытались использовать разные подходы, например, хранить знак числа как отдельный разряд. Оказалось, однако, что при этом неудобно реализовывать даже самые простые операции — сложение и вычитание, потому что приходится учитывать знаковый бит обоих слагаемых. Поэтому создатели компьютеров достаточно быстро пришли к использованию так называемого дополнительного кода⁴⁹.

Чтобы понять, как устроен дополнительный код, вернёмся к нашему примеру с механическим счётчиком. В большинстве случаев такие роликовые цепочки умеют крутиться как вперёд, так и назад, и если прокрутка вперёд давала нам прибавление единицы, то прокрутка назад будет выполнять вычитание единицы. Пусть теперь у нас все ролики выставлены на ноль и мы откручиваем счётчик назад. Результатом этого будет 99999; оно и понятно, ведь когда мы к 99999 прибавили единицу, то получилось 00000, а теперь мы проделали обратную операцию. Говорят, что у нас произошел заём из несуществующего разряда: как и в случае с переносом в несуществующий разряд, если бы у нас был ещё один ролик, всё бы было правильно (например, 100000 — 1 = 99999), но его нет. То же самое происходит и в двоичной системе: если во всех разрядах ячейки были нули (00000000) и мы вычли единицу, получим все единицы: 11111111; если теперь снова прибавить единицу, мы снова получим нули во всех разрядах. Это логично приводит нас к идее использовать в качестве представления числа -1 единицы во всех разрядах двоичного числа, сколько бы ни было у нас таких разрядов. Так, если мы работаем с восьмиразрядными числами, 11111111 у нас теперь означает -1, а не 255; если мы работаем с шестнадцатиразрядными числами, 1111111111111111 теперь будет обозначать, опять-таки, -1, а не 65535 и так далее.

Продолжая операцию по вычитанию единицы над восьмиразрядной ячейкой, мы придём к заключению, что для представления числа -2 нужно использовать 11111110 (раньше это было число 254), для представления -3 — 11111101 (раньше это было 253) и так далее. Иначе говоря, мы волюнтаристски объявили часть комбинаций двоичных разрядов представляющими отрицательные числа вместо положительных, причём всегда новое (отрицательное) значение комбинации разрядов получается из старого (положительного) путём вычитания из него числа 256: 255 — 256 = -1, 254 — 256 = -2 и т. д. (число 256 представляет собой 2⁸, а наши рассуждения верны только для частного случая с восьмиразрядными числами; в общем случае из старого значения нужно вычитать число 2ⁿ, где n — используемая разрядность). Остаётся вопрос, в какой момент остановиться, то есть перестать считать числа отрицательными; иначе, увлёкшись, мы можем дойти до 00000001 и заявить, что это вовсе не 1, а -255. Принято следующее соглашение: если набор двоичных разрядов рассматривается как представление знакового числа, то отрицательнымисчитаются комбинации, старший бит которых равен 1, а остальные комбинации считаются положительными. Таким образом, наибольшее по модулю отрицательное число будет представлено одной единицей в старшем разряде и нулями во всех остальных; в восьмибитном случае это 10000000, -128. Если из этого числа вычесть единицу, получится 01111111; эта комбинация (старший ноль, остальные единицы) считается представлением наибольшего знакового числа и для восьмибитного случая представляет, как несложно видеть, число 127. Как вы уже догадались, прибавление единицы к этому числу снова даст наибольшее по модулю отрицательное. Переход через границу между комбинациями 011...11 и 100...00 для знаковой целочисленной арифметики⁵⁰ представляет собой аналог переноса и займа для несуществующего разряда, который мы наблюдали в арифметике беззнаковой, но называется эта ситуация иначе: переполнение.

Именно такое, а не какое-либо другое расположение границы переполнения даёт две приятные возможности. Во-первых, знак числа можно определить, взяв от него всего один (старший) бит. Во-вторых, оказывается очень простой операция смены знака числа. Чтобы сменить знак числа на противоположный при использовании дополнительного кода, достаточно сменить значения во всех разрядах на противоположные, а к полученному значению прибавить единицу. Например, число 5 представляется следующим восьмибитным знаковым целым: 00000101. Чтобы получить представление числа -5, мы сначала инвертируем все разряды, получаем 11111010; теперь прибавляем единицу и получаем 11111011, это и есть представление числа -5. Для наглядности проделаем смену знака ещё раз: инвертируем все биты в представлении числа -5, получаем 00000100, прибавляем единицу, получаем 00000101, то есть снова число 5, что и требовалось. Как несложно убедиться, для представления нуля операция смены знака инвариантна, то есть ноль остаётся нулём:

Такая же ситуация несколько неожиданно возникает для числа -128 (в восьмибитном случае) или, говоря вообще, для максимального по модулю отрицательного числа заданной разрядности: Это обусловлено отсутствием в данной разрядности положительного числа с таким же модулем, то есть при применении операции замены знака к комбинации 100...00 происходит переполнение.

Если отрицательные числа представлять в дополнительном коде, сложение и вычитание реализуется на аппаратном уровне абсолютно одинаково вне зависимости от знаков слагаемых и даже от самого факта их “знаковости”: мы можем по-прежнему рассматривать все возможные битовые комбинации как представление неотрицательных чисел (то есть вернуться к беззнаковой арифметике), и схематически сложение и вычитание от этого не изменятся. Благодаря этому отпадает надобность в отдельном электронном устройстве для вычитания: операция вычитания может быть реализована как операция прибавления числа, которому сначала сменили знак, причём это, как ни парадоксально, работает и для беззнаковых чисел.

Дело в том, что благодаря переносам в несуществующий разряд и займам из него вычитание числа из другого числа можно выполнить как сложение уменьшаемого с неким другим числом, которое само по себе очень легко вычислить; это число как раз и есть дополнительный код исходного вычитаемого. При этом сложение можно выполнять как если бы числа были беззнаковыми. Пусть нам, к примеру, нужно вычислить разность 75 — 19 на восьмибитных числах. Двоичное представление числа 75 — 01001011, числа 19 — 00010011; инвертировав его и прибавив единицу, получаем 11101101 — представление числа -19. Теперь сложим “столбиком” 01001011 и 11101101, в результате получится двоичное число 100111000₂, которое имеет девять разрядов. Но у нас всего восемь разрядов, поэтому старший разряд при сложении окажется просто отброшен, и мы получим комбинацию 00111000, которая представляет собой двоичное представление числа 56.

Арифметическая основа здесь довольно проста. Сделать побитовую инверсию числа — это то же самое, как вычесть это число из 11111111₂ = 255₁₀; поскольку мы ещё прибавляем единицу, то получается, что при смене знака числа мы заменяем число х на 256 — х. Вместо вычитания у — х мы, получается, выполняем сложение у + (256 — х), но при этом у нас происходит перенос в несуществующий разряд, в результате которого мы теряем 256; окончательный результат составляет у + (256 — х) — 256 = у — х. Этот эффект мы уже обсуждали.

1.6.3. Числа с плавающей точкой

Далеко не любые вычисления можно выполнить в целых числах; точнее, выполнить на самом деле можно любые⁵¹, просто это будет не слишком удобно. Поэтому наряду с целыми числами, представление которых описано в предыдущем параграфе, компьютеры также умеют обрабатывать дробные числа, называемые числами с плавающей точкой. Такие числа предполагают отдельное хранение мантиссы М (двоичной дроби из интервала 1 ≤ М < 2) и машинного порядка Р — целого числа, означающего степень двойки, на которую следует умножить мантиссу. Отдельный бит s выделяется под знак числа: если он равен 1 — число считается отрицательным, иначе положительным. Итоговое число, таким образом, вычисляется как N = (-1)^sМ2^Р. Набор частных соглашений о формате чисел с плавающей точкой, известный как стандарт IEEE-754, в настоящее время используется практически всеми процессорами, способными работать с дробными числами.

Поскольку целая часть мантиссы всегда равна 1, её можно не хранить⁵², используя имеющиеся разряды для хранения цифр дробной части. Для хранения машинного порядка в разное время применялись разные способы (знаковое целое с использованием дополнительного кода, отдельный бит для знака порядка и т. п.); стандарт IEEE-754 предполагает хранение машинного порядка в виде смещённого беззнакового целого числа: соответствующие разряды рассматриваются как целое число без знака, из которого для получения машинного порядка вычитают некоторую константу, называемую смещением машинного порядка.

Стандарт IEEE-754 устанавливает три основных типа чисел с плавающей точкой: число обычной точности, число двойной точности к число повышенной точности⁵³. Число обычной точности занимает в памяти 32 бита, из которых один используется для хранения знака числа, восемь — для хранения смещённого машинного порядка (величина смещения — 127) и оставшиеся 23 — для хранения мантиссы. Число двойной точности занимает 64 бита, причём на машинный порядок отводится 11 бит, а на мантиссу — 52, и смещение машинного порядка составляет 1023. Наконец, число повышенной точности занимает 80 бит, из них 15 бит отведено на машинный порядок со смещением 16383, а оставшиеся 64 составляют мантиссу, причём в этом формате присутствует однобитовая целая часть мантиссы (обычно единица).

Машинный порядок, состоящий из одних нулей или, наоборот, из одних единиц, представляет собой признак особого случая. Порядок, состоящий из одних нулей, означает:

• при мантиссе, состоящей из одних нулей — в зависимости от знакового бита либо ноль, либо “отрицательный ноль” (это различие бывает полезно, если результат очередной операции столь мал по модулю, что его невозможно представить в виде числа с плавающей точкой — тогда мы хотя бы можем сказать, каков был знак результата);

• при мантиссе, содержащей хотя бы одну единицу — денормализованное число, то есть число настолько малое по модулю, что даже при наименьшем возможном значении машинного порядка ни один значащий бит не попал бы в разряды мантиссы.

Порядок, состоящий из одних единиц, может означать следующее:

• при мантиссе, состоящей из одних нулей — “бесконечность” (положительную или отрицательную в зависимости от знакового бита);

• при первом бите мантиссы, установленном в единицу (для 80-битных чисел — при первых двух битах мантиссы, установленных в единицу), а остальных битах мантиссы, установленных в ноль, знаковый бит, равный единице, означает “неопределённость”, а знаковый бит, равный нулю — “не-число типа QNAN” (quiet not-a-number); иногда говорят, что неопределённость есть частный случай QNAN;

• при первом бите мантиссы, равном нулю (для 80-битных — при двух первых битах мантиссы, равных 10) к при наличии в остальной мантиссе единичных битов — “не-число типа SNAN”;

• все остальные ситуации (например, мантисса из одних единиц) означают “неподдерживаемое число”.

Ясно, что даже самые простые арифметические действия над числами с плавающей точкой производятся гораздо сложнее, чем над целыми. Например, чтобы сложить или вычесть два таких числа, необходимо сначала произвести приведение к одному порядку; для этого мантиссу числа, машинный порядок которого меньше, чем у другого, сдвигают вправо на нужное количество позиций. Дальше производится собственно сложение или вычитание, а затем, если результат оказался меньше единицы или больше либо равен 2, его подвергают нормализации, то есть изменяют порядок и одновременно сдвигают мантиссу так, чтобы значение числа не изменилось, но при этом мантисса снова стала удовлетворять условию 1 ≤ М < 2. Аналогичная нормализация производится при перемножении и делении чисел.

Как можно заметить, при любых арифметических операциях над числами с плавающей точкой приходится применять сдвиги мантисс — как влево, так и вправо, и при сдвиге вправо младшие биты мантиссы, которым не нашлось места в отведённых разрядах, просто теряются. Возникающая при этом разница между получившимся результатом и тем, что должно было бы получиться, если бы ничего не отбрасывалось, называется ошибкой округления. Вообще говоря, ошибка округления при действиях с двоичными (как, впрочем, и с десятичными) дробями неизбежна, сколько бы разрядов мы ни отвели под хранение мантиссы, ведь даже обыкновенное деление двух целых чисел, которые образуют несократимую дробь и при этом делитель не является степенью двойки, даст в результате периодическую двоичную дробь, для “точного” хранения которой нам потребовалось бы бесконечное количество памяти. Бесконечным (хотя и периодическим) оказывается представление в виде двоичной дроби таких чисел, как и т. д., так что при переводе их в формат числа с плавающей точкой неизбежно приходится отбрасывать значащие биты. Таким образом, вычисления над числами с плавающей точкой практически всегда дают не точный результат, а приблизительный⁵⁴. В частности, программисты считают неправильным пытаться сравнить два числа с плавающей точкой на строгое равенство, потому что числа могут оказаться “не равны” только из-за ошибок округления.

1.6.4. Тексты и языки

Текстовые данные, то есть информация, представленная в виде, понятном человеку — это, пожалуй, самый универсальный способ работы с информацией, ведь в виде текста человек может описать почти всё, что угодно: выразительной мощности естественных языков, таких как русский или английский, для этого обычно достаточно; философы, объединённые общим направлением под названием “лингвистический позитивизм”, вообще считают, что границы языка совпадают с границами мышления.

Впрочем, здесь возникает одна интересная проблема: в общем случае текст на естественном языке с крайним трудом поддаётся машинному анализу. Проблемами, связанными с таким анализом, занимается целое направление науки — компьютерная лингвистика. Учёные более-менее справились с морфологическим анализом текста на естественном языке, то есть могут заставить компьютерную программу по виду слова и контексту определить, что это за слово и в какой оно находится форме: например, последовательность букв “полка” может означать существительное “полка” в именительном падеже, но с таким же успехом и существительное “полк” в родительном, и без анализа контекста их никак не различить. Условно успешными можно назвать исследования в области синтаксического анализа текста, который приблизительно соответствует школьному “разбору по членам предложения”. Что касается семантического анализа текста на естественном языке, результатом которого должно стать понимание смысла написанного, то не факт, что эта задача вообще когда-нибудь будет решена, и рост вычислительной мощности компьютеров здесь никак не поможет: проблема не в количестве вычислений, а в алгоритмах анализа, сложность которых, судя по всему, превышает человеческие возможности.

Как обычно, если машину не удаётся полностью приспособить к потребностям людей, то людям, напротив, приходится приспосабливаться к возможностям машины. Машину невозможно (и в обозримом будущем не станет возможно) заставить понимать текст на естественном языке, причём виновата здесь, разумеется, не машина — к ней вообще неприменимо понятие “быть виноватым” — а люди, программисты, которые отнюдь не всемогущи. Однако стоит чуть-чуть упростить задачу, задать какие-то достаточно простые формальные правила построения языковых конструкций и предложить людям оформлять тексты в соответствии с этими правилами — и программы, написанные программистами, прекрасно справляются с задачей анализа такого текста.

Когда заданы формальные правила построения текста, в рамках которых человек может задавать информацию так, что компьютерные программы его поймут, говорят, что создан формальный язык — в противоположность естественным языкам, сложившимся в ходе развития цивилизации как средство общения людей между собой. Впрочем, формальные языки не ограничены областью использования компьютеров и возникли намного раньше; примерами формальных знаковых систем являются, в частности, хорошо знакомые нам математические формулы, а также нотные знаки, используемые в музыке, и многое другое.

В общем случае под языком можно понимать всё (обычно бесконечное) множество текстов, которое соответствует установленным правилам, причём для случая естественных языков такие правила оказываются очень и очень сложны, а для формальных языков могут быть совсем простыми, а могут оказаться тоже сравнительно сложными, хотя и не настолько сложными, как правила естественных языков. Конечно, такое понимание языка оказывается несколько огрублённым, поскольку никак не учитывает семантику (то есть, попросту говоря, смысл) текста, ради которого текст, вообще говоря, и существует; тем не менее, когда речь идёт об автоматическом (т. е. компьютерном) анализе текста, до его смысла дело доходит отнюдь не сразу, а на ранних стадиях анализа понимание языка как множества цепочек символов вполне соответствует поставленным задачам.

Чем сложнее правила языка, тем сложнее получается компьютерная программа, предназначенная для его анализа, поэтому формальные языки обычно создаются как результат компромисса между требованиями задачи и возможностями программистов. Например, когда поставлена задача построить график или гистограмму по результатам каких-то измерений или подсчётов, то для представления исходных данных вполне можно использовать язык, предполагающий запись последовательности чисел в десятичной системе счисления, разделённых символом пробела и/или перевода строки, и не допускающий больше ничего. С другой стороны, если поставлена задача написания сложных компьютерных программ, то для этого нужен формальный язык особого вида — язык программирования; некоторые из таких языков бывают чрезвычайно сложны, хотя, конечно, всё равно не могут сравниться по сложности с естественными языками.

Сказанное никоим образом не означает, что компьютер вообще не может работать с текстом на естественном языке; напротив, компьютеры в современных условиях только этим и занимаются. Книга, которую вы читаете, была набрана в текстовом редакторе, её оригинал-макет был подготовлен с помощью системы компьютерной вёрстки; когда вы отправляете и получаете электронную почту и прочие сообщения, читаете сайты в Интернете или электронные книги с помощью карманного ридера — во всех этих случаях мы наблюдаем, как компьютер работает с естественным текстом. Конечно, компьютер не понимает, о чём говорится в книге, или на сайте, или в электронном письме, которое читает пользователь, но это и не требуется: во всех перечисленных случаях задача компьютера состоит лишь в том, чтобы принять текст на естественном языке от одного человека и предъявить другому.

Впрочем, компьютеры (точнее, компьютерные программы) могут проделывать с естественноязычными текстами куда более сложные вещи. Одним из самых эффектных, хотя и отнюдь не самых сложных примеров на эту тему можно считать программы, “поддерживающие беседу” с человеком, первая из которых — “Элиза”⁵⁵ была написана ещё в 1966 году американским учёным Йозефом Вайценбаумом. У человека, сидящего за клавиатурой компьютера, программы типа “Элизы” могут создать впечатление, что “по ту сторону” находится живой человек, хотя люди, которые знают, в чём дело, на самом деле достаточно легко отличают человека от программы, специально создавая разговорную ситуацию, в которой программе не хватает “совершенства”. Примечательно, что такие программы совершенно не вникают в смысл текста, то есть не производят семантического анализа реплик собеседника; вместо этого они анализируют структуру полученных фраз и сами используют слова, полученные от пользователя, для конструирования фраз, смысла которых не понимают.

Спектр существующих формальных языков тоже довольно широк; одних только языков программирования за всю историю компьютеров создано несколько тысяч, хотя далеко не все их них существуют сейчас — многие языки программирования растеряли всех своих сторонников и умерли, как говорится, естественной смертью. Впрочем, поддерживаемых языков программирования, то есть таких, на которых мы могли бы писать программы, если бы захотели, и затем исполнять эти программы на компьютерах, тоже существует по меньшей мере несколько сотен.

Кроме них, широко используются так называемые языки разметки, предназначенные для оформления текстов; пожалуй, самый известный из них — язык HTML, используемый для создания гипертекстовых страниц на сайтах в Интернете. Отметим, что во многих школьных учебниках можно найти совершенно безумное утверждение, что HTML якобы является языком программирования; не верьте.

Наконец, вообще любая компьютерная программа, принимающая на вход информацию в виде текста, самим фактом своего существования задаёт определённый формальный язык, состоящий из всех таких текстов, на которых данная программа отрабатывает без ошибок. Такие языки часто бывают очень и очень примитивными и, как правило, не имеют названия.

При обсуждении формальных языков иногда возникают сомнения, можно ли тот или иной язык считать языком программирования, то есть языком, на котором пишут программы. В некоторых случаях ответ зависит от ответа на вопрос, что такое, собственно говоря, “программа”, причём этот вопрос оказывается не так прост, как кажется на первый взгляд; во всяком случае, существуют такие ситуации, когда на вопрос, является ли некий текст программой или нет, разные люди дают разные ответы. Так, при работе с базами данных довольно популярен язык запросов SQL; встречаются утверждения, что написание запросов на этом языке представляет собой программирование.

Исключить терминологическую неясность позволяет введение более узкого термина; языки, на которых можно записать любой алгоритм, называют алгоритмически полными языками. Поскольку, как мы помним, понятие алгоритма не имеет определения, вместо него используется любой из введённых формализмов, чаще всего машина Тьюринга; с формальной точки зрения алгоритмически полным считают такой язык, на котором можно написать интерпретатор (если угодно, симулятор или модель) машины Тьюринга. Некоторые авторы предпочитают для большей определённости называть такие языки не “алгоритмически полными”, а Тьюринг-полными. Стоит заметить, что алгоритмически полными часто оказываются такие языки, которые с самого начала совершенно не предназначались для написания программ. Так, книга, которую вы читаете, подготовлена с помощью языка разметки TEX, созданного Дональдом Кнутом; этот язык в основном состоит из команд, задающих особенности текста, такие как форма шрифта, размеры и расположение заголовков и иллюстраций и т. п., то есть он изначально не предназначен для программирования; тем не менее язык TEX алгоритмически полон, хотя это знают далеко не все его пользователи.

1.6.5. Текст как формат данных. Кодировки

Текст как таковой, в общезначимом смысле этого слова, на каком бы языке он ни был написан, может быть самыми разными способами представлен в памяти компьютера (в виде содержимого ячеек памяти) и в виде файла на диске. Читателю, возможно, уже приходилось сталкиваться с тем, как редактор текстов при сохранении файла предлагает выбрать, в каком формате его сохранять — в собственном формате данного конкретного текстового редактора или же в формате, предназначенном для последующего прочтения какой-то другой программой, чаще всего каким-то другим редактором текстов.

Среди всех возможных представлений текста особое место занимает формат, именуемый по-английски ASCII-text или plain text; последнее может быть приблизительно переведено как “простой текст”, “чистый текст” или “плоский текст”, тогда как аббревиатура ASCII означает American Standard Code for Information Interchange; это название обозначает кодовую таблицу, которая изначально предназначалась для использования в телеграфии на телетайпах⁵⁶. Таблица ASCII была зафиксирована в 1963 году; на тот момент восьмибитные байты ещё не получили массового распространения, поэтому создатели ASCII отвели на представление одного символа минимально возможное количество бит, позволявшее отличать друг от друга все символы, которые на тот момент были сочтены необходимыми. Исходное задание на разработку стандарта кодовой таблицы подразумевало возможность кодирования 26 заглавных и 26 строчных букв латинского алфавита, 10 арабских цифр, а также некоторого количества знаков препинания (включая, кстати, обыкновенный пробел). К тому же было необходимо предусмотреть несколько так называемых управляющих кодов, которые не обозначали никаких символов, а использовались, например, для управления телетайпом, находящимся по ту сторону линии связи; стандартной была практика отправки сообщения на телетайп, работающий без контроля со стороны людей, например, ночью в запертом здании.

В 64 кодовых значения уложиться не удалось (в самом деле, одних только букв и цифр будет уже 62), поэтому было принято решение использовать семибитную кодировку, то есть для представления одного символа (или управляющего кода) использовать семь двоичных знаков. Всего различных кодов при этом получается 2⁷ = 128. Первым тридцати двум из них, от 0 до 31, отвели роль управляющих, таких как перевод строки (10), возврат каретки (13), табуляция (9) и другие. Код 32 присвоили символу “пробел”; дальше в таблице (см. рис. 1.13) идут знаки препинания и математические символы, занимающие коды с 33 по 47; коды от 48 до 57 соответствуют арабским цифрам от 0 до 9, так что если из кода цифры вычесть 48, мы всегда получим её численное значение (этим мы ещё воспользуемся).

Рис. 1.13. Отображаемые символы ASCII и их десятичные коды

Заглавные латинские буквы располагаются в ASCII-таблице в позициях с 65 по 90 в алфавитном порядке, а позиции с 97 по 122, опять-таки в алфавитном порядке, заняты строчными буквами. Как несложно убедиться, буквы расположены в таблице так, чтобы двоичное представление заглавной буквы отличалось от двоичного представления строчной буквы ровно одним битом (шестым, то есть предпоследним). Так было сделано специально, чтобы облегчить приведение всех символов обрабатываемого текста к одному регистру, например, для выполнения регистро-независимого поиска.

Оставшиеся свободными позиции заняты разнообразными символами, которые на тот момент показались членам рабочей группы, создававшей таблицу, более полезными, чем другие. Последний отображаемый символ ASCII-таблицы имеет код 126 (это тильда, “˜”), а код 127 считается управляющим, как и коды от 0 до 31; этот код, называемый RUBOUT, был изначально предназначен для вычёркивания символа. Дело в том, что в те времена символы часто представлялись пробитыми отверстиями в перфолентах, причём пробитое отверстие соответствовало единице, а непробитое — нулю; перфолента, предназначенная для хранения семибитного текста, имела как раз семь позиций в ширину, то есть каждый символ представлялся ровно одной строчкой из отверстий. Двоичное представление числа 127 состоит из семи единиц, то есть если в любой строке перфоленты “пробить” этот код, получится семь отверстий, причём вне всякой зависимости от того, что там было изначально. При прочтении перфоленты код 127 надлежало пропускать, предполагая, что ранее в этом месте находился символ, который позже был вычеркнут.

Массовый переход к использованию в компьютерах восьмибитных байтов стал причиной возникновения в программировании стойкой ассоциации байта с символом, поскольку, естественно, для хранения одного ASCII-кода стали использовать байт. В то же время появление восьмого бита позволило создать ряд разнообразных расширений ASCII-таблицы, в которых использовались коды из области 128-255. В частности, в разное время и в разных системах использовалось пять (!) различных расширений ASCII, предусматривающих русские буквы (кириллицу). Исторически первой из них была кодировка КОИ8 (код обмена информацией восьмибитный), которая вошла в употребление ещё в середине 1970-х годов на машинах серии ЕС ЭВМ. Основным недостатком этой кодировки является несколько “странный” порядок букв, совершенно не похожий на алфавитный: “ЮАБЦДЕФГХ...” Это затрудняет сортировку строк, требуя лишнего преобразовательного шага, тогда как если символы в таблице располагаются в алфавитном порядке, сортировку можно выполнять, просто сравнивая коды символов в арифметическом смысле.

С другой стороны, именно такой, а не иной порядок букв в таблице КОИ8 имеет вполне определённую причину, которая становится ясна, если выписать строки полученной расширенной ASCII-таблицы по 16 элементов в строке. Оказывается, кириллические буквы в КОИ8 находятся во второй половине 256-кодовой таблицы ровно в тех же позициях, в которых в первой половине таблицы (то есть в исходной таблице ASCII) располагаются их латинские аналоги. Дело в том, что раньше часто встречались (да и до сих пор ещё встречаются) ситуации, когда у текстовых данных кто-то принудительно “отбрасывает” восьмой (старший) бит. КОИ8 — единственная из русских кодировок, которая в такой ситуации сохраняет читаемость. Например, словосочетание “добрый день” при отбрасывании восьмого бита превратится в “DOBRYJ DENX”; читать такой текст не очень удобно, но всё же можно. Именно поэтому кодировка КОИ8 долгое время считалась единственной допустимой в телекоммуникациях и сдала позиции только под натиском Unicode, о котором речь пойдёт ниже. Отметим, что русский алфавит, содержащий 33 буквы, “чуть-чуть не вписался” в две подряд идущие строки по 16 кодов; “не повезло” в этот раз букве “ё”, которую в КОИ8 отправили “на выселки”, приписав её строчному и заглавному варианту коды AЗ₁₆и BЗ₁₆, тогда как все остальные буквы занимают непрерывную область кодов от СО₁₆ до FF₁₆.

В эпоху MS-DOS, то есть в 1980-е годы и в начале 1990-х, на персональных компьютерах самой популярной кодировкой кириллицы была так называемая “альтернативная” русская кодировка, известная также под названием cp866 (кодовая страница №866). В ней, надо сказать, символы тоже располагались не слишком удачно: алфавитный порядок сохранялся, то есть для сортировки её можно было использовать без промежуточных преобразований (за исключением буквы “ё”, которой опять не повезло), но при этом заглавные русские буквы в cp866 шли подряд, тогда как между первыми шестнадцатью и вторыми шестнадцатью строчными вклинились коды для 48 символов псевдографики. Интересно, что эта кодировка до сих пор встречается — например, в некоторых версиях Windows она применяется при работе с консольными приложениями; она же применялась в качестве единственной кодировки кириллицы в системах семейства OS/2.

Во время массового перехода пользователей на системы линейки Windows многие были неприятно удивлены тем, что в этих системах используется ещё одна кодировка кириллицы, совершенно не похожая ни на ср866, ни на КОИ8. Это была кодировка ср1251, содержавшая заодно символы из других кириллических алфавитов — украинского, белорусского, сербского, македонского и болгарского, но при этом её создатели забыли, например, про казахский и многие другие неславянские языки, использующие кириллицу. Отметим, что букве “ё” в очередной раз не повезло — она оказалась вне основной кодовой области.

Компьютеры Apple Macintosh тоже использовали и до сих пор используют свою собственную кодировку, так называемую MacCyrillic. Следует отметить и ещё один “стандарт”, ISO 8859-5, чья кодовая таблица отличается от всех перечисленных; впрочем, этот стандарт, созданный очередным комитетом с совершенно непонятными целями, никогда нигде не применялся.

Можно выделить несколько основных свойств текстового представления данных:

• любой фрагмент текста является текстом;

• объединение нескольких текстов тоже является текстом;

• представление любого символа занимает ровно один байт, что, в частности, позволяет извлечь из текста любой символ по его номеру, не просматривая при этом весь текст;

• представление текста не зависит от архитектуры компьютера, от размера машинного слова, от порядка байтов в представлении целых чисел и от других особенностей, то есть является универсальным для всех компьютеров в мире;

• данные в текстовом формате (текст) могут быть прочитаны человеком на любом компьютере с помощью тысяч различных программ.

С ростом количества известных к используемых в компьютерной обработке информации символов возникла потребность навести в этой области какой-то порядок, в связи с чем в 1987 году был создан реестр Unicode, который часто (и ошибочно) принимают за кодировку. На самом деле основой Unicode является так называемое “универсальное множество символов” (universal characterset, UCS), то есть попросту реестр известных символов, в котором они снабжены номерами; что касается кодировок, то таковых на основе Unicode создано по меньшей мере четыре: UCS-2, UCS-4 (она же UTF-32), UTF-8 и UTF-16.

Кодировки UCS-2 и UCS-4 предполагают использование для хранения одного символа соответственно двух байтов и четырёх. Поскольку к настоящему моменту в реестре Unicode содержится больше 110 000 символов, кодировка UCS-2 с задачей представления любых символов не справляется (два байта могут хранить всего 65536 различных значений, а этого уже давно не хватает) и к настоящему времени считается устаревшей; что касается UCS-4, то её стараются не применять из-за слишком большого и непроизводительного расхода памяти: в самом деле, для хранения большинства символов достаточно одного байта, а больше трёх не нужно вообще никогда к вряд ли когда-нибудь потребуется: странно было бы ожидать, что количество символов в реестре Unicode когда-нибудь превысит 16 с лишним миллионов, ведь в имеющиеся сейчас 110 с небольшим тысяч уже вошли не только все применяющиеся в мире азбуки, включая иероглифические, но и всевозможная экзотика вроде иероглифов древнего Египта и вавилонской клинописи.

Следует отметить, что многобайтовые кодировки полностью лишены большинства из вышеперечисленных достоинств текстового представления данных; их вообще можно рассматривать как текстовые данные с очень большой натяжкой: в самом деле, они даже зависят от порядка байтов в представлении целых чисел; в связи с этим стандарты требуют, чтобы в файле, содержащем “текст” в какой-либо из кодировок на основе Unicode, первые два (или четыре) байта представляли псевдосимвол с кодом FEFF₁₆, что позволяет программе, читающей этот текст, понять, какой порядок байтов использовался при его записи. В результате объединение двух таких “текстов” уже не обязательно представляет собой текст, ведь два исходных текста могут оказаться в разном порядке байтов, а пресловутый FEFF₁₆, встреченный в середине текста, не воспринимается как указание на смену порядка байтов; фрагмент “текста” в многобайтовых кодировках тем более не обязан быть корректным текстом.

В качестве единственного исключения можно рассматривать кодировку UTF-8, которая продолжает использовать для кодирования текстов именно последовательность байтов, а не многобайтовых целых чисел. Более того, первые 127 кодов в ней совпадают с ASCII и считается, что если байт начинается с нулевого бита, то этот байт соответствует однобайтовому коду символа. Таким образом, обычный текст в традиционном формате ASCII оказывается корректным с точки зрения UTF-8 и интерпретируется одинаково как в ASCII, так и в UTF-8. Для символов, не вошедших в ASCII, UTF-8 предполагает использование последовательностей из двух, трёх или четырёх байтов, а при необходимости — и пяти, и шести, хотя пока это не нужно: в Unicodeпросто нет стольких символов.

При этом в UTF-8 байт, начинающийся с битов 110, означает, что мы имеем дело с символом, код которого представлен двумя байтами; первый байт трёхбайтного символа начинается с битов 1110; первый байт четырёхбайтного символа — с битов 11110. Дополнительные байты (второй и последующие в представлении данного символа) начинаются с битов 10. Таким образом, для представления полезной информации в двухбайтовом коде используется 11 битов из 16, в трёхбайтовом — 16 битов из 24, в четырёхбайтовом — 21.

Текст, представленный в UTF-8, не зависит от порядка байтов в целых числах; фрагмент такого текста остаётся корректным, за исключением, возможно, “кусочков” представления одного символа в начале и в конце; объединение двух и более текстов в UTF-8 остаётся текстом в UTF-8. Очевидный недостаток у UTF-8 только один: поскольку для одного символа используются коды переменной длины, для извлечения символа по его номеру приходится просмотреть весь предшествующий ему текст. Кроме того, тексту в UTF-8 присущ недостаток, общий для всех кодировок, основанных на Unicode: никто не может вам гарантировать, что на компьютере, где кто-то попытается прочитать текст, сформированный в UTF-8, в используемом шрифте найдутся корректные изображения для всех символов, которые вы используете. В самом деле, создать шрифт, представляющий сто десять тысяч разнообразных символов, не так просто.

Самой странной из всех кодировок Unicode представляется кодировка UTF-16: она использует двухбайтные числа, но иногда для представления одного символа применяются два таких числа. Эта кодировка не имеет никаких достоинств в сравнении с другими, но обладает всеми их недостатками одновременно; в частности, если нас в принципе устраивает переменная длина кода символа, то гораздо лучше будет использовать UTF-8, ведь она не зависит от порядка байтов к плюс к тому совместима с ASCII, а никаких недостатков по сравнению с UTF-16 у неё нет. При этом именно UTF-16 используется в системах линейки Windows, начиная с Windows-2000; это обусловлено тем, что в более ранних системах линейки, начиная с Windows NT, использовалась UCS-2, тоже предполагающая двухбайтные коды; как мы уже знаем, двух байтов не хватило для представления всех символов Unicode.

Так или иначе, представление текста, основанное на кодировках Unicode, за исключением UTF-8, вообще невозможно рассматривать как текстовые данные в исходном программистском смысле; с UTF-8 в этом плане дела обстоят несколько лучше, однако если ASCII-символы заведомо присутствуют и корректно отображаются в любой операционной среде, то о других символах этого сказать нельзя. Поэтому в ряде случаев использование символов, не вошедших в набор ASCII, считается нежелательным или вообще запрещается; например, это касается текстов компьютерных программ на любых языках программирования.

1.6.6. Бинарные и текстовые данные

При обработке самой разной информации часто возникает выбор, в каком виде представить эту информацию: в текстовом, то есть в таком виде, в котором её сможет прочитать человек, или в бинарном; под бинарным в принципе подразумевается любое представление, отличное от текстового, но обычно данные при этом хранятся в файлах и передаются по компьютерным сетям в том же виде, в котором они представлены в ячейках памяти компьютера во время их обработки программами.

Для того, чтобы уяснить разницу между текстовым и бинарным представлением данных, мы проведём небольшой эксперимент, и в его проведении нам поможет программа hexdump, обычно имеющаяся на любой Unix-системе. Для начала создадим⁵⁷ два файла, в которые запишем последовательность чисел 1000, 2001, 3002, ..., 100099 — то есть всего 100 чисел, каждое следующее больше предыдущего на 1001. Хитрость в том, что эти числа мы в один файл запишем в текстовом представлении, по одному в строке, а в другой файл — в виде четырёхбайтных целых чисел, точно так, как они представляются в памяти компьютера при выполнении всевозможных расчётов. Файлы мы назовём numbers.txt и numbers.bin. Для начала посмотрим, что у нас получилось:

Как видим, двоичный файл получился размером ровно 400 байт, что вполне понятно: мы записали в него 100 чисел по 4 байта каждое. Текстовый файл получился размером 592 байта, то есть чуть больше; он мог бы быть и меньше, если бы мы записали в него, например, числа от 1 до 100, то есть такие числа, представление которых состоит из меньшего количества цифр. Посмотрим, откуда взялось число 592. Числа от 1000 до 9008 имеют в своём текстовом представлении по четыре цифры, и таких чисел девять; числа от 10009 до 99098 имеют по пять цифр каждое, и таких чисел у нас девяносто; последнее число нашей последовательности, 100099, представлено шестью цифрами, и такое число у нас одно. Кроме того, каждое число записано на отдельной строке, а строки, как мы знаем, разделены символом перевода строки (символ с кодом 10); поскольку чисел всего сто, символов перевода строки тоже сто — после каждого числа (в том числе и после последнего; вообще считается, что корректный текстовый файл должен заканчиваться корректной строкой, т. е. последним символом в нём должен быть как раз символ перевода строки). Итого имеем 4 ∙ 9 + 5 ∙ 90 + 6 ∙ 1 + 100 = 36 + 450 + 6 + 100 = 592, что мы и увидели в выдаче команды ls -l.

При этом файл numbers.txt можно выдать на печать, например:

Его также можно открыть в любом текстовом редакторе — если это сделать, мы увидим всё те же сто чисел, точнее, их десятичное представление, и сможем при желании внести изменения. Иначе говоря, мы можем работать с файлом numbers.txt, применяя наши обычные средства работы с текстом.

Иное дело — файл numbers.bin. При попытке выдать его на печать мы увидим откровенную белиберду, что-то вроде такого:

— причём нам ещё повезёт, если наш терминал не придёт в негодность, случайно получив среди всей этой белиберды управляющие последовательности, перепрограммирующие его поведение. Впрочем, привести терминал в чувство можно в любой момент командой reset. Так или иначе, мы видим, что numbers.bin не предназначен для человека; то же самое можно сказать про любой файл, не являющийся текстовым.

Как устроен файл numbers.bin, нам поможет лучше понять программа hexdump, которая позволяет вывести на печать значения байтов заданного файла (в шестнадцатеричной нотации), а при указании дополнительного ключика -С показать ещё и соответствующие байтам символы — точнее, те из них, которые можно отобразить на экране.

Самая левая колонка здесь — это адреса, то есть порядковые номера байтов от начала файла; они идут с интервалом 10₁₆, поскольку каждая строка содержит изображение шестнадцати очередных байтов. Дальше идут, собственно, сами байты, а в колонке справа — символы, коды которых содержатся в соответствующих байтах (или точка, если символ отобразить нельзя). Посмотрев в эту колонку, мы увидим уже знакомую нам белиберду.

Вернувшись к содержимому байтов, вспомним, что числа у нас по условию задачи, во-первых, четырёхбайтные, и, во-вторых, наш компьютер относится к классу little-endian, то есть младший байт числа идёт первым. Взяв первые четыре байта из нашего дампа, мы видим е8 03 00 00; переставив их в обратном порядке, получаем 00000Se8; переводя из шестнадцатеричной системы в десятичную, имеем (с учётом того, что Е обозначает 14): 3 ∙ 16² +14 ∙ 16¹ + 8 ∙ 16⁰ = 768 + 224 + 8 = 1000, это и есть, как мы помним, первое число, записанное в файл. На всякий случай проделаем то же самое для последних четырёх байтов нашего дампа: 0S 87 01 00; переставив их, получаем 00018703₁₆= 1 ∙ 16⁴ + 8 ∙ 16³ + 7 ∙ 16² + 0 ∙ 16¹ + 3 ∙ 16⁰ = 65536 + 8 ∙ 4096 + 7 ∙ 256 + 3 = 100099; как видим, всё сходится.

Для полноты картины применим hexdump к текстовому файлу:

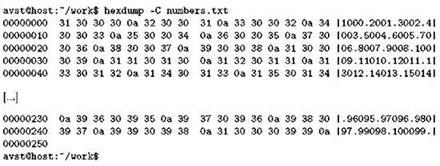
В правой колонке находится вполне читаемый текст, что и понятно, ведь файл как раз текстовый; точками здесь программа hexdump была вынуждена заменить только символы перевода строки. Просматривая значения байтов, начиная с первого, мы видим 31₁₆(десятичное 49) — ASCII-код цифры 1, затем три раза S0₁₆— ASCII-код нуля, потом 0A₁₆ (десятичное 10) — пресловутый символ перевода строки, и так далее.

Такое представление удобно для человека, но программам работать с ним труднее; для проведения каких бы то ни было вычислений числа приходится переводить в то представление, с которым может справиться центральный процессор. Конечно, такое преобразование, как мы увидим позднее, выполнить совсем не трудно, просто о нём необходимо помнить и, конечно же, понимать, что, когда и в каком виде у нас представлено.

1.6.7. Машинный код, компиляторы и интерпретаторы

Как мы уже говорили, практически все современные цифровые вычислительные машины работают по одному и тому же принципу. Вычислительное устройство (собственно сам компьютер) состоит из центрального процессора, оперативной памяти и периферийных устройств. В большинстве случаев все эти компоненты подключаются к общей шине.

Оперативная память состоит из одинаковых ячеек памяти, каждая из которых имеет свой уникальный номер, называемый адресом. Ячейка содержит несколько (чаще всего — восемь) двоичных разрядов, каждый из которых может находиться в одном из двух состояний, обычно обозначаемых как “ноль” и “единица”. Это позволяет ячейке как единому целому находиться в одном из 2ⁿсостояний, где n — количество разрядов в ячейке; так, если разрядов восемь, то возможных состояний ячейки будет 2⁸ = 256, или, иначе говоря, ячейка может “помнить” число от 0 до 255.

В центральном процессоре имеется некоторое количество регистров — схем, напоминающих ячейки памяти; поскольку регистры находятся непосредственно в процессоре, они работают очень быстро, но их количество ограничено, так что использовать регистры следует для хранения самой необходимой информации. Процессор обладает способностью копировать данные из оперативной памяти в регистры и обратно, производить над содержимым регистров арифметические и другие операции; в некоторых случаях операции можно производить и непосредственно с данными в ячейках памяти, не копируя их содержимое в регистры⁵⁸.

Количество информации, которое может обработать процессор в один приём (за одну команду), называется машинным словом. Размер большинства регистров в точности равен машинному слову. В современных системах машинное слово, как правило, больше, чем ячейка памяти; так, машинное слово процессора Pentium составляет 32 бита, то есть четыре восьмибитовые ячейки памяти.

Здесь необходимо сделать одно важное замечание. Процессор Pentium к его современные “наследники”, с которыми мы собираемся работать, являются очередными представителями линейки процессоров х86, и ранние представители этой линейки (до 80286 включительно) были 16-разрядными, то есть их машинное слово составляло 16 бит. Программисты, работающие с этими процессорами на уровне машинных команд, привыкли называть “словом” именно два байта информации, а четыре байта называли “двойным словом”. Когда с выходом очередного процессора размер слова удвоился, программисты не стали менять привычную терминологию, что порождает определённую путаницу. К этому вопросу нам придётся вернуться, когда мы доберёмся до программирования на уровне команд центрального процессора.

Как мы уже знаем (см. § 1.3.2, стр. 55), программа записывается в оперативную память в виде цифровых кодов, обозначающих те или иные операции, а специальный регистр процессора, который называется счётчиком команд (англ. instruction pointer, то есть “указатель на инструкцию”) определяет, из какого места памяти нужно брать инструкции для выполнения. Процессор выполняет цикл обработки команд — то есть извлекает из памяти код очередной команды, увеличивает счётчик команд, дешифрует извлечённый код, исполняет предписанные действия, снова извлекает из памяти очередную команду, и так до бесконечности.

Представление программы, состоящее из кодов машинных команд и, как следствие, “понятное” центральному процессору, называется машинным кодом. Процессор легко может дешифровать такие коды команд, но человеку их запомнить очень трудно, тем более что во многих случаях нужное число приходится вычислять, подставляя в определённые места кодовые цепочки двоичных битов. Вот, например, два байта, записываемые в шестнадцатеричной системе как 01 D8 (соответствующие десятичные значения — 1, 216) обозначают на процессорах Pentiumкоманду “взять число из регистра ЕАХ, прибавить к нему число из регистра ЕВХ, результат сложения поместить обратно в регистр ЕАХ”. Запомнить два числа 01 D8 несложно, но ведь разных команд на процессоре Pentium — несколько сотен, да к тому же здесь сама команда — только первый байт (01), а второй (D8) нам придётся вычислить в уме, вспомнив (или узнав из справочника), что младшие три бита в этом байте обозначают первый регистр (первое слагаемое, а также и место, куда следует записать результат), следующие три бита обозначают второй регистр, а самые старшие два бита здесь должны быть равны единицам, что означает, что оба операнда являются регистрами. Зная (или, опять же, подсмотрев в справочнике), что номер регистра ЕАХ — 0, а номер регистра ЕВХ — 3, мы теперь можем записать двоичное представление нашего байта: 11 011 000 (пробелы вставлены для наглядности), что и даёт в десятичной записи 216, а в шестнадцатеричной — искомое D8.

Если нам потребуется освежить в памяти кусочек нашей программы, написанный два дня назад, то чтобы его прочитать, нам придётся вручную раскладывать байты на составляющие их биты и, сверяясь со справочником, вспоминать, что же какая команда делает. Если программиста заставить составлять программы вот таким вот способом, ничего полезного он не напишет за всю свою жизнь, тем более что в любой, даже самой небольшой, но практически применимой программе таких команд будет несколько тысяч, ну а самые большие программы состоят из десятков миллионов машинных команд.

При работе с языками программирования высокого уровня, такими как Паскаль, Си, Лисп и др., программисту предоставляется возможность написать программу в виде, понятном и удобном для человека, а не для центрального процессора. Процессор такую программу выполнить уже не может, и чтобы всё-таки заставить исполниться программу, написанную на языке высокого уровня, приходится прибегнуть к одному из двух возможных способов трансляции программы. Эти два способа называются компиляцией и интерпретацией.

В первом случае применяют компилятор — программу, принимающую на вход текст программы на языке программирования высокого уровня и выдающую эквивалентный машинный код⁵⁹. Например, в следующей части книги мы будем писать программы на Паскале; набрав текст программы (так называемый исходный текст) и сохранив его в файле, мы будем запускать компилятор Паскаля, который, прочитав текст нашей программы, либо выдаст сообщения об ошибках, либо, если программа написана в соответствии с правилами языка Паскаль, создаст её эквивалент в виде исполняемого файла, в котором будет находиться машинный код нашей программы. Запуская нашу программу, мы потребуем от операционной системы загрузить этот машинный код в оперативную память и передать ему управление, в результате чего процессор выполнит те действия, которые мы описали в виде текста на языке Паскаль.

Следует подчеркнуть, что компилятор — это тоже программа, написанная на каком-то языке программирования; в частности, наш компилятор Паскаля сам, как это ни странно, написан на Паскале, а для компиляции каждой следующей версии его создатели используют предыдущую версию своего же компилятора.

Второй способ исполнения программ, написанных на языках высокого уровня, называется интерпретацией. Программа-интерпретатор прочитывает из файла исходный текст и выполняет предписанные этим текстом действия шаг за шагом, ничего никуда, вообще говоря, не переводя. Современные интерпретаторы обычно для удобства и увеличения скорости выполнения создают какое-то своё внутреннее представление нашей программы, но с машинным кодом такое представление не имеет ничего общего.

Отметим, что из одного школьного учебника в другой кочует совершенно бредовая фраза, что якобы интерпретатор переводит программу в машинный код пошагово и тут же этот код выполняет. Если вам что-то подобное говорили или вы сами такое прочитали в какой-нибудь очередной не пойми кем написанной книжке (пусть даже имеющей гриф министерства образования, бывает и такое) — не верьте, вас в очередной раз обманывают! На современных машинах и при работе под управлением современных операционных систем так вообще невозможно сделать, поскольку даже если мы сформируем какой-то машинный код, записать его мы можем только в область памяти, предназначенную для хранения данных (как мы увидим позже, область машинного кода во время работы программы не может быть изменена), а передать управление на этот код мы не сможем, так как исполнение команд из области, предназначенной для данных, тоже запрещено. В общем, даже если бы мы хотели так сделать, то ничего бы не получилось — но самое интересное, что так делать вовсе не нужно! Интерпретатор сам по себе является программой, и он может просто выполнить нужные действия, никуда, ни в какой код их не переводя. Тот странный человек, который первым придумал фразу про пошаговый перевод в машинный код с немедленным исполнением, сам, очевидно, никогда никаких программ не писал, иначе такая сумасшедшая идея просто не пришла бы ему в голову.

С одним интерпретатором мы уже сталкивались: это командный интерпретатор, обрабатывающий команды, которые мы набираем в командной строке. Как мы видели в § 1.4.13, на языке этого интерпретатора, который называется Bourne Shell, можно писать вполне настоящие программы. Другие интерпретаторы мы пока рассматривать не будем, но вообще интерпретируемое исполнение характерно для широкого круга языков программирования, таких как Перл, Пайтон, Руби, Лисп и многих других.

Интересно заметить, что в наше время границы между компиляцией и интерпретацией постепенно размываются. Многие компиляторы переводят программу не в машинный код, а в некое промежуточное представление, обычно называемое “байт-кодом”; именно так работают компиляторы языков Java и С#. Во многих случаях компиляторы порождают такой код, который уже во время исполнения осуществляет интерпретацию какой-то части промежуточного представления программы. С другой стороны, интерпретаторы с целью повышения эффективности работы тоже переводят программу в промежуточное представление, которое, правда, затем выполняют сами. Существуют компиляторы, вроде бы создающие отдельный исполняемый файл, но при внимательном рассмотрении этого файла оказывается, что в него целиком включён интерпретатор внутреннего представления программы плюс само это представление.

Так или иначе, при компилируемом исполнении часто используются элементы интерпретации, а при интерпретируемом — элементы компиляции, и встаёт вопрос о том, где между этими двумя подходами провести границу и существует ли такая граница вообще. Мы рискнём предложить довольно простой ответ на этот вопрос, позволяющий в каждом конкретном случае определённо сказать, имеет здесь место компилируемое или интерпретируемое исполнение. Интерпретатор во время исполнения интерпретируемой программы сам вынужден находиться в памяти, тогда как компилятор нужен лишь на этапе компиляции, а исполняться программа может без его участия.

Программирование на языках высокого уровня удобно, но, к сожалению, не всегда применимо. Причины могут быть самые разные. Например, язык высокого уровня может не учитывать некоторые особенности конкретного процессора, либо программиста может не устраивать тот конкретный способ, которым компилятор реализует те или иные конструкции исходного языка с помощью машинных кодов. В этих случаях приходится отказаться от языка высокого уровня и составить программу в виде конкретной последовательности машинных команд. Однако, как мы уже видели, составлять программу непосредственно в машинных кодах очень и очень сложно. И здесь на помощь приходит программа, называемая ассемблером.

Ассемблер — это частный случай компилятора: программа, принимающая на вход текст, содержащий условные обозначения машинных команд, удобные для человека, и переводящий эти обозначения в последовательность соответствующих кодов машинных команд, понятных процессору. В отличие от самих машинных команд, их условные обозначения, называемые также мнемониками, запомнить сравнительно легко. Так, команда из приведённого ранее примера, код которой, как мы с некоторым трудом выяснили, равен 01 D8, в условных обозначениях⁶⁰выглядит так:

Здесь нам уже не надо заучивать числовой код команды и вычислять в уме обозначения операндов, достаточно запомнить, что словом add обозначается сложение, причём в таких случаях всегда первым после обозначения команды стоит первое слагаемое (не обязательно регистр, это может быть и область памяти), вторым — второе слагаемое (это может быть и регистр, и область памяти, и просто число), а результат всегда заносится на место первого слагаемого. Язык таких условных обозначений (мнемоник) называется языком ассемблера.

Программирование на языке ассемблера коренным образом отличается от программирования на языках высокого уровня. На языке высокого уровня (на том же Паскале) мы задаём лишь общие указания, а компилятор волен сам выбирать, каким именно способом их исполнить — например, какими регистрами и ячейками памяти воспользоваться для хранения промежуточных результатов, какой применить алгоритм для выполнения какой-нибудь нетривиальной инструкции и т. д. С целью оптимизации быстродействия компилятор может переставить инструкции местами, заменить одни на другие — лишь бы результат остался неизменным. В программе на языке ассемблера мы совершенно однозначно и недвусмысленно указываем, из каких машинных команд будет состоять наша программа, и никакой свободы ассемблер (в отличие от компилятора языка высокого уровня) не имеет.

В отличие от машинных кодов, мнемоники доступны для человека, то есть программист может работать с мнемониками без особого труда, но это не означает, что программировать на языке ассемблера просто. Действие, на описание которого мы бы потратили один оператор языка высокого уровня, может потребовать десятка, если не сотни строк на языке ассемблера, а в некоторых случаях и больше. Дело тут в том, что компилятор языка высокого уровня содержит большой набор готовых “рецептов” решения часто возникающих небольших задач и предоставляет все эти “рецепты” программисту в виде удобных высокоуровневых конструкций; ассемблер же ничего подобного не содержит, так что в нашем распоряжении оказываются только возможности процессора.

Интересно, что для одного процессора может существовать несколько разных ассемблеров. На первый взгляд это кажется странным, ведь не может же один и тот же процессор работать с разными системами машинных кодов (так называемыми системами команд). В действительности ничего странного здесь нет, достаточно вспомнить, что же такое на самом деле ассемблер. Система команд процессора, разумеется, не может измениться (если только не взять другой процессор). Однако для одних и тех же команд можно придумать разные обозначения; так, уже знакомая нам команда add еах, ebx в обозначениях, принятых в компании AT&T, будет выглядеть как addl %ebx, %еах — и мнемоника другая, и регистры не так обозначены, и операнды не в том порядке, хотя получаемый машинный код, разумеется, строго тот же самый — 01 D8. Кроме того, при программировании на языке ассемблера мы обычно пишем не только мнемоники машинных команд, но и директивы, представляющие собой прямые приказы ассемблеру. Следуя таким указаниям, ассемблер может зарезервировать память, объявить ту или иную метку видимой из других модулей программы, перейти к генерации другой секции программы, вычислить (прямо во время ассемблирования) какое-нибудь выражение и даже сам (следуя, разумеется, нашим указаниям) “написать” фрагмент программы на языке ассемблера, который сам же потом и обработает. Набор таких директив, поддерживаемых ассемблером, тоже может быть разным, как по возможностям, так и по синтаксису.

Поскольку ассемблер — это не более чем программа, написанная вполне обыкновенными программистами, никто не мешает другим программистам написать свою программу-ассемблер, что часто и происходит. Ассемблер NASM, который рассматривается во втором томе нашей книги — это один из ассемблеров, существующих для процессоров семейства 80x86; существуют и другие ассемблеры для этих процессоров.

---

¹Это следует даже из его названия: английское слово computer буквально переводится как “вычислитель”, а официальный русский термин “ЭВМ” образован от слов “электронная вычислительная машина”.

²На самом деле известно более ранее описание разностной машины — в книге немецкого инженера Иоганна фон Мюллера, изданной в 1788 году. Использовал ли Беббидж идеи из этой книги, достоверно не известно.

³Менабреа достаточно много своих работ публиковал именно на французском, который в те времена был более популярен в качестве международного, нежели английский.

⁴Ада Лавлейс была единственным законным ребёнком поэта Байрона, но отец видел свою дочь всего один раз в жизни, через месяц после её рождения. Согласно наиболее правдоподобной версии, своё пристрастие к математике Ада переняла от своей матери, Анны Изабеллы Байрон. В число знакомых Ады Лавлейс входили, кроме Чарльза Беббиджа, такие знаменитости, как Майкл Фарадей и Чарльз Диккенс, а её наставницей в юности была знаменитая женщина-учёный Мэри Сомервилль.

⁵Фото с сайта Википедии; оригинал может быть загружен со страницы https://en.wikipedia.Org/wiki/File:Dubulttriode_darbiibaa.jpg. Используемые здесь и далее изображения с сайтов фонда Wikimedia разрешены к распространению под различными вариантами лицензий Creative Commons; подробную информацию, а также оригиналы изображений в существенно лучшем качестве можно получить на соответствующих веб-страницах. В дальнейшем мы опускаем подробное замечание, ограничиваясь только ссылкой на веб-страницы, содержащие оригинальное изображение.

⁶По одной из версий, основной целью Черчилля было не допустить огласки того факта, что о массовых бомбардировках города Ковентри ему было известно заранее из перехваченных шифрограмм, но он ничего по этому поводу не предпринял, чтобы не выдать возможностей Британии по вскрытию немецких шифров; впрочем, мнения историков на этот счёт расходятся. Более того, версию о сознательном принесении Ковентри в жертву опровергает ряд свидетельств непосредственных участников событий того времени. Вопрос, зачем было уже после завершения войны уничтожать технику, использовавшуюся для вскрытия шифров, остаётся открытым.

⁷Американский проект создания атомной бомбы.

⁸Фото с сайта Викимедиа Коммонс; http://commons.wikimedia.org/wiki/File:KL_CoreMemory_Macro.jpg.

⁹Как ни странно, за минувшие сорок лет никаких качественно новых усовершенствований не предложено. Японский проект “компьютеров пятого поколения” существенных результатов не дал, тем более что опирался он не на технологическое развитие аппаратной базы, а на альтернативное направление развития программного обеспечения.

¹⁰Английское название этого регистра— instruction pointer, то есть “указатель на инструкцию”; устоявшийся в русскоязычной литературе термин “счётчик команд”, как и оригинальный термин program counter, использовавшийся, например, на PDP, не столь удачен, ведь этот “счётчик” на самом деле ничего не считает.

¹¹Выражение вида “нечто указывает на ячейку памяти” является синонимом выражения “нечто содержит адрес ячейки памяти”.

¹²Фактически при этом в компьютере имеются две разные шины — одна для ячеек памяти, вторая для контроллеров.

¹³На самом деле в случае с диском всё будет несколько сложнее; более подробное обсуждение происходящего оставим до части нашей книги, посвящённой операционным системам.

¹⁴Можно также встретить термины “основная память” и “оперативное запоминающее устройство” (ОЗУ). В англоязычной литературе используется термин RAM (Random Access Memory), который можно перевести как “память произвольного доступа”.

¹⁵То есть общая стоимость хранения, поделенная на объём хранимой информации.

¹⁶Под конечным пользователем обычно подразумевают человека, который с помощью компьютеров решает какие-то свои задачи, никак не связанные с дальнейшим использованием компьютеров; например, секретарь или дизайнер, используя компьютер, являются при этом конечными пользователями, а программист — нет, поскольку задачи, которые он решает, нацелены на организацию работы других пользователей (или даже его самого) с компьютером. Вполне возможно, что конечными пользователями окажутся те, кто будет использовать программу, которую сейчас пишет программист.

¹⁷Интересно отметить, что в русском языке слово “телетайп” прочно закрепилось в качестве нарицательного обозначения соответствующих устройств, тогда как в англоязычных источниках чаще используется термин “телепринтер” (teleprinter); дело в том, что слово teletype являлось зарегистрированной торговой маркой одного из производителей такого оборудования.

¹⁸Фото с сайта Википедии, см. http://en.wikipedia.org/wiki/File:ASR- 33_at_CHM.agr.jpg

²⁰Там же, см. http://en.wikipedia.Org/wiki/File:DEC_VT100_terminal.jpg

¹⁹В наше время в ходу термин “папка”; этот термин, на самом деле означающий элемент графического интерфейса — то самое “окошко с иконками” — неприемлем для именования объекта файловой системы, содержащего имена файлов. В частности, папки совершенно не обязательно как-либо представлены на диске, а иконки в них не обязаны соответствовать файлам; в то же время с файлами и каталогами можно работать без “папок” — ни двухпанельные файловые менеджеры, ни командная строка никаких “папок” не подразумевают. В этой книге мы используем корректную терминологию; термины “каталог” и “директория” мы считаем равноправными, а слово “папка”, кроме этой сноски, вам больше нигде в тексте не встретится.

²¹Эта информация была актуальна на момент написания книги в начале 2016 года. Вполне возможно, что к тому времени, когда вы будете читать этот текст, ситуация изменится. Так или иначе, в Интернете на форумах всегда найдутся люди, готовые помочь очередному неофиту.

²²В некоторых системах может потребоваться другая команда; за информацией обращайтесь к вашему системному администратору.

²³Здесь и далее в примерах команд, когда необходимо показать и саму команду, и её вывод, мы будем перед командой добавлять символ приглашения командной строки “$”. Настоящее приглашение командной строки обычно длиннее, оно может содержать имя пользователя, название машины, на который вы работаете, и текущий каталог, что очень удобно; в некоторых примерах мы для наглядности будем использовать более сложное приглашение, но пока для краткости ограничимся одним символом.

²⁴Читатель, привыкший к традиционной терминологии мира Windows, может удивиться использованию термина “суффикс” вместо “расширения”. Дело здесь в том, что в MS-DOS и ранних версиях Windows“расширение” файла было намертво связано с его типом и рассматривалось обособленно от имени, тогда как в системах семейства Unix окончание имени файла никогда не играло такой роли и всегда было просто частью имени.

²⁵Это верно для ОС Linux и FreeBSD. В других ОС, например в SunOS/Solaris, ключи команды ps имеют совершенно иной смысл.

²⁶От английского background — “фон”.

²⁷От английского foreground — “передний план”.

²⁸ В английском оригинале — permissions.

²⁹Подробно о системах счисления будет рассказано в § 1.5.2; в принципе, для работы с правами доступа к файлам не обязательно понимать, как в действительности устроена восьмеричная система счисления, достаточно просто помнить, какой вид прав соответствует какой цифре (4, 2, 1) и что итоговое обозначение режима доступа составляет их сумму, которая, естественно, оказывается цифрой от 0 до 7.

³⁰Обратите внимание, что число записано с нулём впереди; согласно правилам языка Си это означает, что число записано в восьмеричной системе, а поскольку профессиональные пользователи Unix очень любят этот язык, они обычно записывают восьмеричные и шестнадцатеричные числа, следуя соглашениям Си и никак это не оговаривая, то есть предполагая, что их и так поймут.

³¹Сокращение английских слов change mode, то есть “изменить режим”.

³²Надо сказать, что twm в системе присутствует практически всегда, чего о других оконных менеджерах не скажешь.

³³Всего существует несколько десятков оконных менеджеров, так что приведённый список не может претендовать на полноту.

³⁴Это отличается от поведения в Windows, где для перемещения фокуса ввода необходимо выбрать окно, щёлкнув по нему мышкой, при этом окно обязательно показывается полностью.

³⁵Другие подходы возможны; например, довольно часто в литературе упоминается система счисления, использующая три цифры, значения которых — 0, 1 и -1; такие системы счисления мы оставим за рамками нашей книги, но заинтересованный читатель легко найдёт их описания в других источниках.

³⁶Здесь и далее в записи позиционных дробей мы будем использовать для отделения дробной части точку, а не запятую, как это обычно делается в русскоязычной литературе. Дело в том, что в английских текстах в этой роли всегда использовалась именно точка, в результате чего она же используется во всех существующих языках программирования. Занимаясь программированием, следует приучить себя к мысли, что никакой “десятичной запятой” не бывает, а бывает “десятичная точка”.

³⁷От слова Boolean, по имени английского математика Джорджа Буля, который впервые предложил формальную систему, известную сейчас как алгебра логики, или булева алгебра.

³⁸На всякий случай напомним, что иррациональным называется число, которое не может быть представлено в виде дроби m/n, где m — целое, а n — натуральное; примером такого числа может служить √2. Очень важно не делать при этом распространённую, но от этого не менее чудовищную ошибку, записывая в “иррациональные” все бесконечные десятичные дроби, такие как 1/3 или 2/7. “Бесконечность” периодических дробей на самом деле обусловлена выбором системы счисления и не имеет никакого отношения к свойству числа как такового; так, в системе счисления по основанию 21 обе упомянутые дроби будут иметь конечное “21-ичное” представление, тогда как 1/2 окажется дробью бесконечной.

³⁹Здесь встречается очевидное возражение, что в будущем могут появиться символы, которые мы не включили в V; однако при ближайшем рассмотрении ничего от этого не меняется, достаточно придумать какой-нибудь способ обозначения таких символов через символы уже имеющиеся. Например, можно придумать какой-нибудь специальный символ, после которого обычными десятичными цифрами будет указываться номер “нового” символа, и эти номера присваивать всем новым символам по мере их появления. Больше того, можно вообще рассматривать алфавит из двух символов 0 и 1, а все остальные символы кодировать комбинациями нулей и единиц; собственно говоря, в памяти компьютеров всё именно так и происходит.

⁴⁰Напомним, что под алфавитом можно понимать произвольное конечное множество, как правило, состоящее хотя бы из двух элементов, хотя в некоторых задачах рассматриваются также и алфавиты из одного символа. Пустым алфавит быть не может.

⁴¹Почему это столь обязательно, мы узнаем чуть позже.

⁴²Когда речь идёт об алгоритмах или фрагментах программ, под рекурсией понимают использование таким алгоритмом (или таким фрагментом программы) самого себя для решения более простого случая задачи.

⁴³Автор не претендует на лавры изобретателя этого варианта алгоритма, поскольку точно помнит, что ему это решение в студенческие годы рассказал кто-то из старшекурсников, занимавшихся на одном с ним спецсеминаре, но кто это был, за давностью лет вспомнить несколько затруднительно.

⁴⁴3дравствуй, мир! (англ.)

⁴⁵Здесь мы проводим рассуждения по упрощённой схеме — в частности, не делаем различия между алгоритмом и его записью; кроме того, мы говорим об “алгоритме вообще”, тогда как с формальной точки зрения следовало бы использовать один из строго определённых формализмов, хотя бы ту же самую машину Тьюринга. Всё это несложно исправить, но лаконичность изложения от этого сильно пострадает, а наша задача сейчас — не в том, чтобы дать формальное доказательство, а в том, чтобы объяснить, почему дела обстоят так, а не иначе.

⁴⁶Читателю, заинтересовавшемуся вычислимыми функциями, мы можем порекомендовать для начала книгу В. Босса “От Диофанта до Тьюринга” [6], содержащую довольно удачный популярный обзор соответствующей математической теории. Существуют, разумеется, и более специальные пособия. Более подробное изложение теории алгоритмов и вычислимости мы оставим за рамками нашей книги, чтобы не пытаться объять необъятное.

⁴⁷Отметим, что “оператор примитивной рекурсии” использует целочисленный параметр, который на каждом рекурсивном обращении уменьшается на единицу, так что количество оставшихся рекурсивных обращений всегда в точности равно этому параметру.

⁴⁸“Термины” big-endians и little-endians введены Джонатаном Свифтом в книге “Путешествия Гулливера” для обозначения непримиримых сторонников разбивания яиц соответственно с тупого конца и с острого. На русский язык эти названия обычно переводились как “тупоконечники” и “остроконечники”. Аргументы в пользу той или иной архитектуры действительно часто напоминают священную войну остроконечников с тупоконечниками.

⁴⁹Английский термин — two’s complement, то есть “двоичное дополнение”.

⁵⁰То есть когда сумма двух положительных оказывается отрицательной и наоборот.

⁵¹В самом деле, с помощью целых чисел очевидным образом можно представлять числа рациональные (в виде дроби числитель/знаменатель), либо воспользоваться концепцией так называемых чисел с фиксированной точкой, когда считается, что целое число представляет не единицы, а, скажем, стотысячные доли обрабатываемой величины.

⁵²За исключением нескольких особых случаев, о которых речь пойдёт дальше.

⁵³Соответствующие англоязычные термины — single precision, double precision и extended precision.

⁵⁴Между прочим, автору этих строк неоднократно встречалось утверждение о том, что вообще любые вычисления на компьютере производятся с ошибками; как можно догадаться, источником этой ахинеи стали всё те же школьные учебники информатики. Не верьте, вас обманывают! Вычисления в целых числах компьютер производит абсолютно точно.

⁵⁵По одной из версий, программа была названа в честь героини пьесы “Пигмалион” Бернарда Шоу; нечто общее тут действительно прослеживается, ведь в пьесе профессор Хиггинс обучает Элизу правильно произносить слова, но поначалу совершенно упускает из виду прочие аспекты, отличающие даму высшего общества от девушки-цветочницы.

⁵⁶С этими устройствами мы уже сталкивались в § 1.4.1.

⁵⁷Эти файлы вы найдёте в архиве примеров к этой книге; программы на Паскале, которые можно использовать для генерации этих двух файлов, будут приведены в § 2.12.

⁵⁸Наличие или отсутствие такой возможности зависит от конкретного процессора; так, процессоры Pentium могут, минуя регистры, прибавить заданное число к содержимому заданной ячейки памяти и произвести некоторые другие операции, тогда как процессоры SPARC, применявшиеся в компьютерах фирмы Sun Microsystems, умели только копировать содержимое ячейки памяти в регистр или, наоборот, содержимое регистра в ячейку памяти, но никаких других операций над ячейками памяти выполнять могли.

⁵⁹Вообще говоря, компилятор — это программа, переводящая программы с одного языка на другой; перевод на язык машинного кода — это лишь частный случай, хотя и очень важный.

⁶⁰Здесь и далее используются условные обозначения, соответствующие ассемблеру NASM, если не сказано иное; подробно ассемблер NASM будет рассматриваться в следующем томе нашей книги.