Задачи на кодирование, решаемые с применением недесятичных систем счисления - Системы счисления

Конспект

Система счисления — знаковая система, позволяющая по определенным правилам записывать числа при помощи символов некоторого алфавита.

Как правило, символами алфавита системы счисления являются десятичные цифры. Однако это — лишь результат общепринятой договорённости; формально такими символами могут быть любые знаки, в том числе произвольные буквы (пример — использование латинских букв от А до F в качестве цифр шестнадцатеричной системы счисления).

Примеры наиболее часто используемых систем счисления:

Система счисления	Основание (Р)	Алфавит системы счисления	Пример записи числа
Двоичная	2	0, 1	1011012
Восьмеричная	8	0, 1, 2, 3, 4, 5, 6, 7	123458
Десятичная	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9	123410
Шестнадцатеричная	16	0, 1,2, 3,4,5, 6, 7, 8, 9, А (=10), В (=11), С (=12), D (=13), Е (=14), F (=15)	F4D916

Во многих задачах, в условиях которых не говорится о необходимости преобразования чисел в другую систему счисления или о выполнении арифметических операций в различных системах счисления, можно найти аналогию с той или иной позиционной системой счисления и этим облегчить решение задачи.

Для решения приведённых ниже задач необходимо уметь выполнять перевод чисел из десятичной системы счисления в троичную и обратно.

Перевод числа из троичной системы счисления в десятичную осуществляется путём выполнения вычислений по развёрнутой записи исходного числа.

Пример. Требуется перевести в десятичную систему счисления число 12021₃:

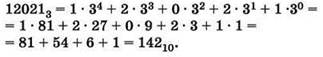
Перевод целого десятичного числа в троичную систему счисления выполняется путём последовательного деления с остатком числа на основание системы счисления (3) с последующей записью полученного результата и остатков на каждом шаге деления в порядке, обратном порядку их получения. Деление производится до тех пор, пока полученный на очередном шаге результат не будет меньше основания системы счисления.

Пример: требуется перевести число 12345₁₀ в троичную систему счисления:

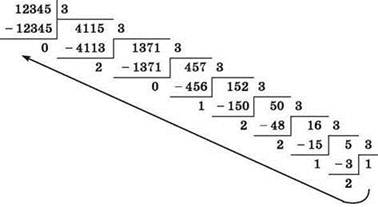
В результате: 12345₁₀ = 121221020₃.

Разбор типовых задач

Задача 1.

Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке.

Вот начало списка:

1. ААААА

2. ААААО

3. ААААУ

4. АААОА

... ...

Запишите слово, которое стоит на 240-м месте от начала списка.

Решение

Поскольку слова начинаются с букв А и их список начинается с ААААА, а далее идут слова ААААО, ААААУ, АААОА и т.д., буквы А, О, У сопоставляются цифрам: А - 0, O - 1, У - 2. В результате исходная задача сводится к следующей:

Все 5-значные числа, составленные из цифр 0, 1, 2, записаны в порядке возрастания. Вот начало списка:

1. 00000

2. 00001

3. 00002

4. 00010

... ...

Какое число стоит на 240-м месте в списке?

Чтобы определить число, стоящее в списке на 240-й позиции, нужно учесть “рассогласование” между значениями чисел и их порядковыми номерами в списке:

• последовательность чисел начинается с значения 00000₃ = 0₁₀;

• нумерация чисел в списке начинается с единицы. Тогда для определения числа, стоящего в 240-й позиции, составляется следующее соответствие:

Порядковый номер	Значение числа
1	0
240	(240 - 1)

Очевидно, что на 240-м месте в списке стоит десятичное число 239 (так как значение числа на 1 меньше, чем порядковый номер).

Пятиразрядная запись этого числа в троичной системе счисления определяется:

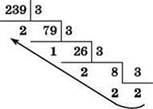
В результате, на 240-м месте в списке находится пятиразрядное троичное число 22212.

Преобразуя это число к записи слова, кодируемого буквами А, О, У по правилу соответствия: А-0, O-1, У-2, получается слово: УУУОУ.

Ответ: УУУОУ.

Задача 2.

Все 5-буквенные слова составлены из букв К, О, Т. Вот начало списка:

1. ТТТОК

2. ТТТКT

3. ТТТКО

4. ТТТКК

5. ТТОТТ

... ...

На каком месте списка находится слово КОТОК?

Решение

В приведённом списке после слова ТТТОК идёт слово ТТТКТ, потом ТТТКО, затем — ТТТКК и ТТОТТ. Тогда сопоставив буквы К, О, Т цифрам: Т-0, O-1, К-2, условие задачи переписывается в виде:

Все 5-значные числа составлены из цифр 0, 1, 2. Вот начало списка:

1. 00012

2. 00020

3. 00021

4. 00022

5. 00100

... ...

На каком месте списка находится число 21012?

Число 21012 записано в троичной системе счисления. После преобразования его в десятичное:

Чтобы определить номер позиции в списке для числа 192, учитывается “рассогласование” между значениями чисел и их порядковыми номерами в списке:

• последовательность чисел начинается с 12₃ = 5;

• нумерация чисел в списке начинается с единицы. Для определения номера позиции числа 192 составляется соответствие:

Порядковый номер	Значение числа
1 (= 5 – 4)	5
(192 - 4)	192

Очевидно, что десятичное число 192 будет стоять в списке на 188-м месте (так как значение числа на 4 больше, чем порядковый номер).

Ответ: на 188-м месте.

Задача 3.

Сколько существует различных символьных последовательностей длины 5 в трёхбуквенном алфавите {К, О, Т}, которые содержат ровно две буквы О?

Решение (способ 1)

Задача подобна предыдущим и принцип её решения будет во многом аналогичным — путём “перевода” букв в цифры соответствующей системы счисления и работы с полученными числами.

1) Поскольку никаких слов изначально не задано, мы можем сами “назначить” цифры, соответствующие каждой букве. А поскольку букв в алфавите три, мы имеем дело с троичной системой счисления и выберем следующие соответствия букв и цифр:

O - 0, К - 1, Т - 2.

(Мы выбрали нуль именно для буквы О, так как нам понадобится искать слова, содержащие ровно две буквы О, а с нулями это окажется проще.)

2) Итак, речь идёт об определении количества пятиразрядных троичных чисел (причём незначащие нули слева важны!), содержащих ровно два нуля.

3) Первый нуль может быть в одной из 5 позиций — получаем 5 вариантов.

В каждом из этих вариантов второй нуль может располагаться так:

• когда первый нуль находится в позиции “1”, второй нуль может располагаться в одной из 4 оставшихся позиций— “2”, “3”, “4”, “5”;

• когда первый нуль находится в позиции “2”, второй нуль может располагаться в одной из 3 оставшихся позиций правее — “3”, “4” и “5” (ведь ситуацию, когда нули располагаются в позициях “1” и “2”, мы уже рассмотрели перед этим);

• когда первый нуль находится в позиции “3”, второй нуль может располагаться в одной из 2 оставшихся позиций правее — “4” и “5” (почему, — рассмотрено выше);

• когда первый нуль находится в позиции “4”, второй нуль может располагаться только в 1 позиции правее — “5”.

Итого получаем 4 + 3 + 2 + 1 = 10 вариантов размещения в пятиразрядном числе двух нулей.

Возможны и другие рассуждения, приводящие к тому же результату.

Условно обозначим наши нули разными цветами: например, первый — синим, а второй — красным.

Тогда синий нуль можно разместить в пяти разрядах — получаем 5 вариантов. И в каждом из этих пяти вариантов красный нуль можно разместить в любой из оставшихся четырёх позиций — т.е. по четырём вариантам. Значит, всего получаем 5 ∙ 4 = 20 вариантов размещения наших разноцветных нулей.

Но теперь вспомним, что на самом деле оба нуля (синий и красный) — совершенно равноправны. А значит, пары “синий — красный” и “красный — синий” (если читать число слева направо) — это одни и те же пары. Следовательно, каждая такая пара посчитана дважды, и всего вариантов размещения в пятиразрядном числе двух одинаковых нулей будет 10.

4) Итак, существует 10 вариантов размещения в числе двух нулей. В каждом из этих 10 вариантов остаётся три цифры, которые могут быть равны или 1, или 2.

Сколько может быть таких неповторяющихся комбинаций? Очевидно, столько, сколько может быть различных трёхразрядных чисел в системе счисления, состоящей из двух цифр (т.е. двоичной). Значит, для каждого из 10 ранее найденных вариантов получается 2³ = 8 “подвариантов”.

Количество различных n-разрядных чисел в системе счисления с основанием т определяется по формуле: mⁿ (основание системы счисления, возведенное в степень, равную числу разрядов).

Тогда общее число троичных чисел, в которых из пяти цифр ровно две — нулевые, будет равно 8 ∙ 10 = 80.

Решение (способ 2)

Другой возможный способ решения — использование формул комбинаторики.

1) В последовательности из 5 букв должно быть две буквы О и, соответственно, три других буквы. Сначала ищем количество перестановок с повторениями из двух букв О и трёх произвольных букв (обозначим их символом “#”).

Формула для вычисления количества перестановок с повторениями:

где n_∑ — общее количество букв в слове, n₁ — количество обязательных букв (в данном случае — букв О), n₂ — количество прочих букв (т.е. знаков #). Знак “I” обозначает вычисление факториала (произведение всех натуральных чисел от 1 до n:

В данной задаче количество перестановок с повторениями будет равно:

2) В остальных трёх позициях слова (кроме тех, что заняты двумя буквами О) может стоять любая из двух оставшихся букв — К или Т. Следовательно, нужно вычислить количество всех возможных трёхбуквенных слов, состоящих из двух возможных букв.

Такое трёхбуквенное слово можно рассматривать как трёхразрядное число, которое представлено в системе счисления с основанием 2 (так как в алфавите этой “системы счисления” всего две “цифры” — К и Т). Тогда количество таких слов совпадает с количеством возможных различных трёхразрядных двоичных чисел. А оно равно 2³ = 8.

Количество различных n-разрядных чисел в системе счисления с основанием m определяется по формуле: mⁿ (основание системы счисления, возведенное в степень, равную числу разрядов).

Ответ: 80.

Задача 4.

Составляется таблица кодовых слов для передачи сообщений, где каждому сообщению должно быть сопоставлено отдельное кодовое слово из 4 букв. В этих кодовых словах можно использовать только пять букв: “Л”, “О”, “Г”, “И”, “К”, при этом буква “Л” может быть использована ровно один раз, а все остальные буквы могут встречаться в кодовом слове сколько угодно раз (или отсутствовать).

Сколько различных кодовых слов можно получить по этой таблице?

Решение

1. Выпишем все возможные варианты 4-буквенных кодовых слов с ровно одной буквой “Л”: Л***, *Л**, **Л* или ***Л (где * обозначает любые другие буквы). Получили 4 возможных варианта.

2. Вариантов распределения четырёх оставшихся в нашем алфавите букв в трёх позициях кодовых слов столько же, сколько возможно трёхзначных чисел в системе счисления с основанием 4, т.е. 4³ = 64.

3. Тогда всего возможных кодовых слов: 4 ∙ 64 = 256.

Ответ: 256.