Информатика и ИКТ подготовка к ЕГЭ
Решение заданий части А и В варианта № 1 - Решения - Учебно-тренировочные тесты
Решение заданий части А и В варианта № 1
А1. 12410 = 11111002. В двоичной записи данного числа содержится 5 единиц.
Ответ: 5.
А2. На основе данных таблицы построим граф путей из пункта А в пункт F (без возвратов в уже пройденный пункт). При построении графа будем учитывать кратчайший путь до рассматриваемого пункта, отбрасывая более длинные пути. Около каждой дуги графа будем указывать длину соответствующего пути.
По первой строке таблицы определяем, что из пункта А можно попасть только в пункт В. Далее, из пункта В (без возврата) можно попасть в пункты С, D и Е. (см. рис. 92, а).
Пути из А в Е, проходящие через вершины В, С и через вершины Б, D (см. рис. 92, b), длиннее пути, проходящего через пункты A, В и Е (18 > 9 и 20 > 9). Следовательно, из дальнейшего рассмотрения пути A → B → C → E и A → B → D → E, можно исключить.
Путь из А в F, проходящий через пункты В, D (см. рис. 92, b), длиннее пути, проходящего через пункты В, С (16 > 14). Следовательно, путь А → В → В → А из дальнейшего рассмотрения так же исключаем.
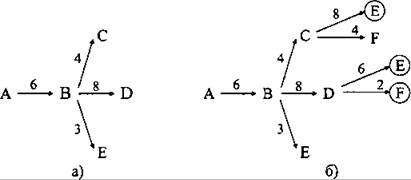
Рис. 92.
Из пункта Е (без возврата) можно попасть в пункты С, D и F (см. рис. 93).
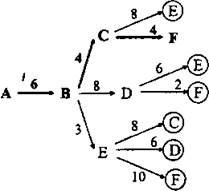
Рис. 93.
Путь А → В → Е → С длиннее пути А → В → С (17 > 10). Путь А → В → Е → D из дальнейшего рассмотрения можно исключить, так как пути проходящие через этот пункт длиннее рассмотренных.
И, наконец, из оставшихся путей A → B → E → F и А → В → С → А второй короче (19 > 14). Следовательно, длина искомого пути равна 14.
Ответ: 14.
А3. 1) Пусть ![]() Тогда при x1 = 1, х2 = 1, х3 = 1, х4 = 0, х5 = 0, х6 = 0, F = 0, что не соответствует третьей строке таблицы.
Тогда при x1 = 1, х2 = 1, х3 = 1, х4 = 0, х5 = 0, х6 = 0, F = 0, что не соответствует третьей строке таблицы.
2) Пусть ![]() Значения F соответствуют при всех предложенных комбинациях x1, х2, х3, х4 х5 и хб.
Значения F соответствуют при всех предложенных комбинациях x1, х2, х3, х4 х5 и хб.
3) Пусть ![]() Тогда, например, при x1 = 1, х2 = 1, х3 = 1, х4 = 0, х5 = 0, х6 = 0, F = 0, что не соответствует третьей строке таблицы.
Тогда, например, при x1 = 1, х2 = 1, х3 = 1, х4 = 0, х5 = 0, х6 = 0, F = 0, что не соответствует третьей строке таблицы.
4) Пусть ![]() Тогда, например, при x1 = 1, х2 = 1, х3 = 1, х4 = 0, х5 = 0, х6 = 1, F = 0, что не соответствует второй строке таблицы.
Тогда, например, при x1 = 1, х2 = 1, х3 = 1, х4 = 0, х5 = 0, х6 = 1, F = 0, что не соответствует второй строке таблицы.
Ответ: ![]()
А4. 1) По маске ?af*r.t?? не будут отобраны файлы affair.tex и after.txt, поскольку первые символ маски «?а» означают, что в начале имени стоит один любой символ, за которым следует буква «а».
2) Согласно маске *af?r.?t? расширение файла должно содержать символ «t», перед и после которого должно содержаться по символу. Следовательно по этой маске не будут отобраны файлы wafer.txt, affair.tex и after.txt.
3) Маска *af*r.t?? означает, что имя файла должно содержать последовательность подряд идущих символов «af» перед которой может быть произвольное количество символов (в том числе пустое), а после через произвольное количество символов (в том числе пустое) должен быть расположен символ «r». Расширение файла должно начинаться с символа «t», после которого должно находиться два символа. Из предложенных шести файлов по этой маске будут отобраны wafer.txt, affair.tex и after.txt.
4) Согласно маске *af*.??t расширение файла должно содержать символ «t», перед которым должно содержаться два символа. Следовательно по этой маске не будет отобран файлaffair.tex.
Ответ: *af*r.t??.
А5. 1) Шестнадцатиричное число САН состоит из шестнадцатеричных цифр С, А, 1 и 1, следовательно может являться только результатом сложения четырёхзначных чисел.
2) Шестнадцатиричное число 1198 состоит из шестнадцатеричных цифр 1, 1, 9 и 8, поэтому так же может являться только результатом сложения четырёхзначных чисел.
3) В числе 9АС шестнадцатеричные цифры 9, А и С расположены в порядке возрастания.
3) В числе F98 шестнадцатеричные цифры F, 9 и 8 расположены в порядке убывания. Это число может являться результатом работы автомата.
Ответ: F98.
А6. По первой таблице определяем, что Клочко Р. Ч. соответствует ID — 37. В первом столбце второй таблицы находим ID родителя 37 и по второму столбцу этой таблицы находим значения ID его детей: 74 и 94. Теперь в первом столбце второй таблицы находим ID родителей 74 и 94. Здесь ID 94 отсутствует, а для ID 74 во втором столбце таблицы находим ID детей: 47 и 11.
По первой таблице определяем, что ID 47 соответствует человеку мужского пола, а для ID 11 в графе «Пол» указано значение «ж». Значит Белых А. В. является внучкой Клочко Р. Ч.
Ответ: Белых А. В.
А7. В результате копирования ячейки С2 в ячейку D1, с учётом абсолютной адресации, получим формулу = 2*$А1—CS3. Значение, получаемое по формуле = $А$2+В3, расположенной в ячейке С3, равно 8. Следовательно в ячейке D1 получим значение 8(= 2*8—8).
Ответ: 8.
А8. Частота дискретизации звука — это количество измерений уровня звукового сигнала (при записи) за одну секунду. Одно измерение за одну секунду соответствует частоте 1 Гц. Соответственно, 44 кГц — 44000 измерений за 1 секунду. Разрешение (разрядность регистра) — число бит в регистре аудиоадаптера.
Размер (в байтах) цифрового моноаудиофайла (А) можно оценить по формуле: А = D*T*I/8, где D — количество измерений уровня звукового сигнала (при записи) за одну секунду, Т — время звучания или записи звука (с), I — разрядность регистра (разрешение, бит). Согласно условию задачи D = 24000 (изм. в с), Т = 3 мин = 180 с, I = 32 бита.
Следовательно А = 24000 ∙ 180 ∙ 32/8 = 17280000 байт ≈ 16,48 Мбайт. Из приведённых величин наиболее близка к размеру полученного файла —16 Мбайт.
Ответ: 16 Мбайт.
А9. В задаче рассматривается код неравномерной длины.
Код является однозначно декодируемым, если любое слово, составленное из кодовых слов, можно декодировать только единственным способом.
Префиксный код — код, в котором никакое кодовое слово не является началом (префиксом) другого. Аналогично можно определить постфиксный код — это код, в котором никакое кодовое слово не является концом (постфиксом) другого.
Префиксный и постфиксный коды являются однозначно декодируемыми.
Рассмотрим предложенные варианты сокращения для одной из букв длины кодового слова.
Если код буквы Б поменять на 10, то кодовые слова букв А — 01, Б — 10, В — 110, Г - 001, Д — 111 образуют префиксный код. Следовательно, код можно однозначно декодировать.
Теперь покажем, что оставшиеся сокращения кодовых слов не позволят составить однозначно декодируемый код. (Это необходимо сделать, чтобы убедиться, что другие варианты ответов не подходят.)
Если код буквы В поменять на 10, оставив без изменения коды остальных букв: А — 01, Б — 101, Г - 001, Д - 111, то возникнет неоднозначность при декодировании, например, двоичной последовательности 101001. Здесь возможны два варианта декодирования: ВВА и БГ.
Если код буквы Г поменять на 0, оставив без изменения коды остальных букв: А - 01, Б - 101, В - 110, Д — 111, то возникнет неоднозначность при декодировании, например, двоичной последовательности 0101. Здесь возможны два варианта декодирования: АА и ГБ.
Ответ: для буквы Б - 10.
А10. Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное (когда истинная посылка влечёт ложное заключение). Значит, для решения задачи, нужно выбрать такое X, что X > 8 и X не делится на 5. Из предложенных чисел таким числом является 9.
Ответ: 9.
A11. Наименьшее количество бит, которым можно закодировать не менее 30 символов: 20 различных букв и 10 десятичных цифр. То есть найти такое наименьшее натуральное число iV, при котором 2N ≥ 30. Так как 24 < 30 < 25, то минимальное количество бит, необходимое для кодирования 30 символов, равно 5. Значит, для кодирования одного символа требуется 5 бит. Номер состоит из 8 символов. Для его кодирования потребуется 5 * 8 = 40 бит. Поскольку номер кодируется минимально возможным количеством байт, то для его кодирования используют 5 байт. Следовательно, для 30 номеров отводится 5 * 30 = 150 байт.
Ответ: 150 байт.
А12. В результате выполнения первого цикла элементы массива примут значения от —2 до 10. То есть, элемент массива ао будет равен —2(=0-2),
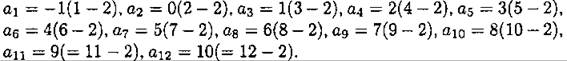
В результате выполнения второго цикла
при i = 12 элемент массива ![]()
при i = 11 элемент массива ![]()
при i = 10 элемент массива ![]()
при i = 9 элемент массива ![]()
при i = 8 элемент массива ![]()
при i = 7 элемент массива ![]()
при i = 6 элемент массива ![]()
при i = 5 элемент массива ![]()
при i = 4 элемент массива ![]()
при i = 3 элемент массива ![]()
при i = 2 элемент массива ![]()
Значения элементов a11 и a12 не изменятся. Таким образом, все элементы, кроме двух последних, будут сдвинуты на два элемента вправо.
Ответ: все элементы, кроме двух последних, будут сдвинуты на два элемента вправо.
А13. Согласно предложенному алгоритму РОБОТ будет двигаться сначала вправо, до тех пор, пока там нет препятствия, затем вверх, до тех пор кока нет препятствия сверху, далее снова вправо (при отсутствии справа препятствия), затем вверх (при отсутствии препятствия сверху) и т. д.
РОБОТ остановится только тогда, когда в текущей клетке и справа, и сверху будет находится стена. Таким клеткам на рисунке 1 соответствуют те, у которых верхняя и правая грань очерчены жирной линией. Помимо заштрихованной клетки таковыми являются С3, Е5 и F1.
В клетку С3 РОБОТ может попасть из А3, В3, С3; в Е5 — из А5, В5, С5, D5, Е5; в F1 — из А1, В1, С1, D1, Е1 и F1. Всего таких клеток 14. Из остальных клеток в результате выполнения алгоритма, можно попасть в заштрихованную. Так как всего клеток 36, то условию задачи удовлетворяют 36 - 14 = 22 клетки.
Ответ: 22.
В1. В 1-байтной кодировке информационный объём сообщения длиной 208 символов равен 208 байт. В 16-битном коде (2-байтной кодировке) информационный объём этого сообщения равен 2 ∙ 208 = 516 байт. Следовательно, после перекодировки информационный объём сообщения увеличился на 208 байт = 208 * 8 = 1664 бит.
Ответ: 1664.
В2. Изобразим с помощью графа, при помощи каких команд может быть получено число 25 и числа, предшествующие ему (см. рис. 94). При этом учитываем, что количество команд не должно превышать 5-ти.
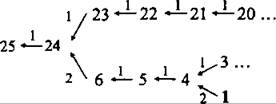
Рис. 94.
По графу определяем, что число 1 можно преобразовать в число 25, путём выполнения последовательности 5-ти команд: 21121.
Ответ: 21121.
В3. Для решения задачи выполним программу по шагам, занося значения переменных в таблицу:
|
Выполняемый оператор |
Истинность условия |
Значения переменных |
|
|
k |
5 |
||
|
k:= 9 |
— |
9 |
— |
|
s:= 43 |
— |
9 |
43 |
|
s > 0 |
да |
9 |
43 |
|
k:= k — 1 |
— |
8 |
43 |
|
s:= s — 2 * k |
- |
8 |
27(= 43 — 2 * 8) |
|
s > 0 |
да |
8 |
27 |
|
k:= k — 1 |
— |
7 |
27 |
|
s:= s — 2 * k |
— |
7 |
13(= 27 – 2 * 7) |
|
s > 0 |
да |
7 |
13 |
|
k:= k — 1 |
— |
6 |
13 |
|
s:= s — 2 * k |
— |
6 |
1(= 13 – 2 * 6) |
|
s > 0 |
да |
6 |
1 |
|
k:= k — 1 |
- |
5 |
1 |
|
s:= s — 2 * k |
— |
5 |
—9(= 1 – 2 * 5) |
|
s > 0 |
нет |
5 |
-9 |
|
writeln(k) |
— |
5 |
-9 |
Таким образом, значение переменной к после выполнения фрагмента алгоритма равно 5.
Ответ: 5.
В4. Для составления слов используется 4 различных буквы. Поставим в соответствие каждой из букв цифры системы счисления с основанием 4 (с учётом порядка их следования в алфавите): А — О, К — 1, O — 2, С — 3. Тогда, упорядоченной по алфавиту последовательности слов
1. АААА
2. АААК
3. АААО
4. АААС
5. ААКА
...
будут соответствовать числа в системе счисления с основанием 4:
1. 00004 = 010
2. 00014 = 110
3. 00024 = 210
4. 00034 = 310
5. 00104 = 410
Заметим, что соответствующая последовательность чисел, записанных в десятичной системе счисления на 1 меньше номера строки, содержащей данное число. Значит на 154 месте будет находиться десятичное число 153. Четырёхзначное число в системе счисления с основанием 4, равное 15310, имеет представление ![]()
Далее подберём числа а, b, с, d так, чтобы полученное число в системе счисления с основанием 4 было равно 15310.
При a = 0 наибольшее число в системе счисления с основанием 4 имеет вид ![]() Следовательно a > 0.
Следовательно a > 0.
При a = 1 наибольшее число в системе счисления с основанием 4 имеет вид ![]() Следовательно a > 1.
Следовательно a > 1.
При a = 2 наибольшее число в системе счисления с основанием 4 имеет вид ![]() а наименьшее — 20004 = 12810. Следовательно a = 2.
а наименьшее — 20004 = 12810. Следовательно a = 2.
При a = 2, b = 3 наименьшее число в системе счисления с основанием 4 имеет вид ![]() Следовательно b < 3.
Следовательно b < 3.
При a = 2, b = 2 наименьшее число в системе счисления с основанием 4 имеет вид ![]() Следовательно b < 2.
Следовательно b < 2.
При a = 2, b = 1 наименьшее число в системе счисления с основанием 4 имеет вид ![]() а наибольшее — 21334 = 15910. Следовательно a = 2, b = 1.
а наибольшее — 21334 = 15910. Следовательно a = 2, b = 1.
При а = 2, b = 1, с = 3 наименьшее число в системе счисления с основанием 4 имеет вид ![]() Следовательно с < 3.
Следовательно с < 3.
При а = 2, b = 1, с = 2 наименьшее число в системе счисления с основанием 4 имеет вид ![]() Следовательно с = 2. А искомое число имеет вид 212410 = 15310. Соответствующее слово имеет вид ОКОК.
Следовательно с = 2. А искомое число имеет вид 212410 = 15310. Соответствующее слово имеет вид ОКОК.
Ответ: ОКОК.
В5. Обозначим через х значение ячейки С1. Тогда, по данным таблицы, ячейке А2 будет соответствовать значение 24(= 2 ∙ (5 + 7)), ячейке В2 — 3 ∙ (5 + я), ячейке С2 — 24(= 2 ∙ 2 ∙ (1 + 5)). Диаграмма на рисунке 2 представляет собой круг, разбитый на три равные части, каждой из которых соответствуют значения ячеек А2, В2 и С2. Следовательно, значение ячейки В2 равно 24 = 3 ∙ (5 + х), отсюда, х = 3.
Ответ: 3.
В6. Для решения задачи выполним программу по шагам, занося значения переменных в таблицу:
|
Выполняемый оператор |
Истинность условия |
Значения переменных |
||
|
а |
b |
с |
||
|
а := 15 |
— |
15 |
— |
— |
|
b := 6 |
— |
15 |
6 |
— |
|
а :=4 * b — а |
— |
9 (=4 ∙ 6—15) |
6 |
— |
|
а < b |
нет |
9 |
6 |
— |
|
с := 2 * а — b |
— |
9 |
6 |
12 (= 2 ∙ 9 - 6) |
Таким образом, значение переменной с после выполнения фрагмента алгоритма равно 12.
Ответ: 12.
В7. Проанализируем, что происходит в результате выполнения данной программы. Для этого в качестве х рассмотрим произвольное целое число, входящее в диапазон типа объявленной переменной (в нашем случае —32768 ≤ х ≤ 32767), например, 412.
|
Выполняемый оператор |
x |
а |
b |
|
|
readln(х) |
412 |
— |
— |
|
|
а : = 0 |
412 |
0 |
— |
|
|
о и & |
412 |
0 |
0 |
|
|
логическое условие х > 0 истинно (412 > 0) |
||||
|
а := а + 1 |
412 |
1 |
0 |
|
|
b := b + 2*(х mod 10) |
412 |
1 |
4(= 0 + 2 ∙ 2) |
|
|
х := х div 10 |
41 |
1 |
4 |
|
|
логическое условие х > 0 истинно (41 > 0) |
||||
|
а := а + 1 |
41 |
2 |
4 |
|
|
b := b + 2*(х mod 10) |
41 |
2 |
6(= 4 + 2 ∙ 1) |
|
|
х := х div 10 |
4 |
2 |
2 |
|
|
логическое условие х > 0 истинно(4 > 0) |
||||
|
а := а + 1 |
4 |
3 |
2 |
|
|
b := b + 2*(х mod 10) |
4 |
3 |
12(= 6 + 2 ∙ 3) |
|
|
х := х div 10 |
0 |
3 |
12 |
|
|
логическое условие х > 0 ложно (0 |
||||
|
writeln(a) |
0 |
3 |
12 |
|
|
writeln(b) |
0 |
3 |
12 |
|
Заметим, что а принимает значение равное, соответствующее количеству разрядов в числе х, а переменная b — сумме удвоенных цифр числа х.
Из условия задачи следует: 1) a = 3, значит исходное число х — трёхзначное; 2) b = 24, значит в исходном числе х, сумма удвоенных цифр равна 24. Следовательно сумма цифр числа х равна 12.
В наибольшем из таких чисел х цифра, стоящая в разряде сотен, должна быть наибольшая, то есть 9. Тогда, сумма цифр, стоящих в разрядах десятков и единиц равна 12 — 9 = 3. В разряде десятков должна быть наибольшая цифра, которая в сумме с цифрой разряда единиц даёт 3, то есть в разряде десятков должна быть цифра 3. Следовательно в разряде единиц — 0. Значит, числом х, удовлетворяющим условию задачи является 930.
Ответ: 930.
В8. Согласно условию ![]() где р искомое основание. Решая уравнение относительно неизвестно р находим р = 8.
где р искомое основание. Решая уравнение относительно неизвестно р находим р = 8.
Ответ: 8.
В9. Построим граф, соответствующий данной схеме дорог. На графе будем для каждого города отмечать все возможные перемещения в города, связанные с ним исходящими дорогами (см. рис. 95).
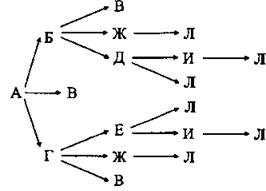
Рис. 95.
По графу определяем, что существует всего 6 различных путей.
Ответ: 6.
В10. В случае А на сжатие файла потребуется 45 секунд. Объём сжатого файла будет равен 50 * 0,65 = 32,5 Мбайт = 32,5 ∙ 223 бит. На передачу сжатого файла потребуется 32,5 ∙ 223/218= 1040 секунд. На распаковку файла — 15 секунд. Итого 45 + 1040 + 15 = 1100 секунд.
В случае Б объём исходного файла равен 50 Мбайт = 50 ∙ 223 бит. На передачу этого файла потребуется 50 ∙ 223/218 = 1600 секунд.
Следовательно, способ А быстрее на 1600 - 1100 = 500 секунд.
Ответ: А500.
В11. В результате применения поразрядной конъюнкции к заданному IP-адресу узла и маске получим
Заметим, что 255ю имеет представление 111111112. Следовательно, в результате поразрядной конъюнкции этого числа с любым другим числом х, получим х. Значит в результате применения поразрядной конъюнкции к числам 255 и 176 получим 176; к числам 255 и 154 получим 154.
Число 010 имеет представление 000000002. Следовательно, в результате поразрядной конъюнкции числа 0 с любым другим числом я, получим 0. Значит, применяя поразрядную конъюнкцию к числам 0 и 89 получим 0.
Остается рассмотреть порязрядную конъюнкцию чисел 112 и 124. Число 112ю имеет представление 011100002, число 12410 имеет представление 011111002. Поразрядная конъюнкция этих чисел 011111002 = 11210.
Таким образом, искомый адрес сети 176.154.112.0. Согласно кодировке таблицы EADG.
Ответ: EADG.
В12. Страницы, найденные по запросу Физика | Задачи, соответствуют объединению множеств страниц, содержащих ключевые слова Физика и Задачи, а по запросу Физика & Задачи соответствуют пересечению этих множеств.
Так как всего страниц, содержащих каждое из этих слов, равно 7 270 + 8 550 = 15 820 (тыс.), а количество страниц, содержащих хотя бы одно из этих слов (объединение множеств), равно 12 450 (тыс.), то количество страниц, содержащих одновременно оба слова Физика и Задачи (пересечение множеств), равно 15 820 - 12 450 = 3 370 (тыс.).
Следовательно по запросу Физика & Задачи будет найдено 3 370 (тыс. страниц).
Ответ: 3 370.
В13. Выполнение команды Вперед 6, соответствует тому, что из текущей координаты на числовой оси исполнитель будет передвигаться на 6 единиц вправо, то есть для определения нового положения, следует к текущему значению прибавить 6. Аналогично, выполнение команды Назад 4, соответствует тому, что из текущей координаты на числовой оси исполнитель будет передвигаться на 4 единицы влево, и для определения нового положения следует от текущего значения вычесть 4.
1) Если Белка будет 12 раз выполнять только команду Вперед 6, то значение 51 на числовой оси, соответствующее положению в конце выполнения алгоритма, можно определить как результат сложения числа 2 (начальное положение исполнителя) и суммы, состоящей из 12-ти слагаемых, каждым из которых является 6.
Всего должно быть выполнено 12 различных команд, значит, количество различных числовых значений, в которых может остановиться Белка после выполнения различных программ, соответствует количеству различных сумм, состоящих из слагаемых 6 и —4 (начальное положение исполнителя не влияет на это количество).
Такими суммами являются:
1) сумма, в которой каждое из 12-ти слагаемых число 6,
![]()
2) сумма, в которой ровно одно из 12-ти слагаемых число —4,
![]()
3) сумма, в которой ровно два из 12-ти слагаемых число —4,
![]()
...
12) сумма, в которой ровно одиннадцать из 12-ти слагаемых число —4,
![]()
13) сумма, в которой все двенадцать слагаемых число —4,
![]()
Значит, количество различных числовых значений, в которых может остановиться исполнитель Белка после выполнения различных программ равно 13.
Ответ: 13.
В14. Фрагмент программы:
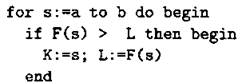
осуществляет поиск наибольшего значения функции F(s) в целочисленных точках промежутка от —16 до 16 и выводит на экран точку, в которой достигается это значение.
Заметим, что графиком функции F(x) = (3 - х)(х + 7) — 1 является парабола, ветви которой направлены вниз. Вершина этой параболы лежит в точке х = -2. Эта точка принадлежит промежутку [-16; 16]. Следовательно, наибольшее значение функция достигает в точке х = -2.
Ответ: —2.
В15. Первое и второе уравнения системы представляют собой конъюнкцию четырёх высказываний. Конъюнкция истинна (равна единице) только в том случае, когда каждое из высказываний, связанных конъюнкцией, истинно. Значит каждая из импликаций ![]()
![]() должна быть истинной. Импликация ложна только в одном случае, когда посылка истинна (1), а заключение ложно (0).
должна быть истинной. Импликация ложна только в одном случае, когда посылка истинна (1), а заключение ложно (0).
То есть, для логических переменных, входящих в первое уравнение имеем: если значение логической переменной ![]() то xi+1 может принимать два значения 0 и 1. Если же
то xi+1 может принимать два значения 0 и 1. Если же ![]() то
то ![]()
Для удобства дальнейших рассуждений представим эти данные в виде схемы 1.
Схема 1
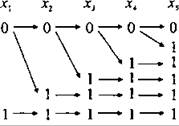
Для логических переменных, входящих во второе уравнение имеем: если значение логической переменной ![]() то её отрицание ¬yi = 0, следовательно, yi+1 может принимать два значения 0 и 1. Если же yi = 0, то
то её отрицание ¬yi = 0, следовательно, yi+1 может принимать два значения 0 и 1. Если же yi = 0, то ![]() то
то ![]() . Для удобства дальнейших рассуждений представим эти данные в виде схемы 2.
. Для удобства дальнейших рассуждений представим эти данные в виде схемы 2.
Третье уравнение эквивалентно следующему уравнению: ![]()
Первому и второму уравнениям удовлетворяет 6 ∙ 13 = 78 различных наборов логических переменных. Из них третьему уравнению не удовлетворяют те, у которых x1 = 1, y1 = 0. Таких наборов 1 ∙ 5 = 5.
Схема 2
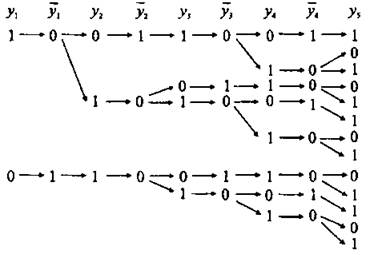
Значит, всего система имеет 78 - 5 = 73 различных решений.
Ответ: 73.