Информатика и ИКТ подготовка к ЕГЭ
Вероятностный подход - Количество информации - Кодирование информации - Краткий теоретический справочник
Определение. Количество информации можно рассматривать как меру уменьшения неопределённости знания при получении информационных сообщений.
За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределённость знания в два раза. Такая единица названа битом.
Пусть N — общее число возможных исходов какого-то процесса, и из них интересующее нас событие может произойти К раз. Тогда вероятность этого события равна K/N. Вероятность выражается в долях единицы.
Количество информации для событий с различными вероятностями определяется по формуле
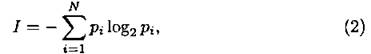
где I — количество информации, N — количество возможных событий, pi — вероятности отдельных событий.
Если события равновероятны, то количество информации определяется по формуле
![]()
или из уравнения
![]()
Пример 1. В корзине лежат 8 мячей разного цвета (красный, синий, жёлтый, зелёный, оранжевый, фиолетовый, белый, коричневый). Какое количество информации несёт в себе сообщение о том, что из корзины будет вынут мяч красного цвета?
Решение. Так как возможности вынуть мяч каждого из имеющихся цветов равновероятны, то для определения количества информации, содержащегося в сообщении о выпадении мяча красного цвета, воспользуемся формулой (3): I = log2 N = log2 8 = 3 (бита).
Ответ: 3 бита.
Пример 2. В корзине лежат 16 мячей разного цвета: 4 красных, 8 синих, 4 жёлтых. Какое количество информации несёт в себе сообщение о том, что из корзины извлечён один мяч?
Решение. Так как количество мячей различных цветов неодинаково, то вероятности зрительных сообщений о цвете вынутого мяча различны. Для определения этих вероятностей разделим количество мячей одного цвета на общее количество мячей. Получим вероятность вынуть мяч красного цвета рк = 4/16 = 0,25, синего цвета рс = 8/16 = 0,5, жёлтого цвета рж — 4/16 = 0,25.
Так как события не являются равновероятными, то воспользуемся формулой (1):
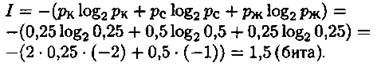
Ответ: 1,5 бита.
Количество информации, содержащейся в алфавитном сообщении
Если алфавит состоит из N символов, то количество информации, которое несёт один символ, можно определить по формуле (2), или в случае, если считать, что появление каждого символа — события равновероятные — по формулам (3—4).
Чтобы определить количество информации, содержащейся в сообщении, записанном в некотором алфавите, следует количество информации, которое несёт в себе один символ этого алфавита, умножить на число символов в сообщении.
Пример 3. Известно, что объём сообщения составляет 3 Кб. Определите мощность алфавита, с помощью которого записано это сообщение, если известно, что оно содержит 3072 символа.
Решение. Объём данного сообщения равен 3 Кб = 3 ∙ 1024 ∙ 8 бит = 24576 бит. Тогда на один символ приходится 24576 : 3072 = 3. По формуле (4) определяем количество символов в рассматриваемом алфавите: N = 21 = 23 = 8.
Ответ: 8 символов.