Алгоритмы - Разработка и применение - 2016 год
Отрицательные циклы в графе - Динамическое программирование
До настоящего времени при рассмотрении алгоритма Беллмана-Форда мы предполагали, что граф содержит ребра с отрицательной стоимостью, но не имеет отрицательных циклов. А теперь рассмотрим более общий случай графа, который может содержать отрицательные циклы.
Задача
Для начала зададим себе два естественных вопроса:
♦ Как определить, содержит ли граф отрицательный цикл?
♦ Как найти отрицательный цикл в графе, в котором он присутствует? Алгоритм, разработанный для поиска отрицательных циклов, также приводит к улучшению практической реализации алгоритма Беллмана-Форда из предыдущих разделов.
Оказывается, идеи, описанные ранее, позволяют найти отрицательные циклы, которые имеют путь, достигающий конечной точки t. Но прежде чем углубляться в подробности, сравним задачу нахождения отрицательного цикла, способного достичь заданного t, с более естественной (казалось бы) задачей нахождения отрицательного цикла в любом месте графа независимо от его расположения относительно конечной точки. Как выясняется, разработка решения первой задачи позволяет также получить решение второй задачи следующим образом. Предположим, мы начинаем с графа G, добавляем в него новый узел t и соединяем каждый из остальных узлов v в графе с узлом t через ребро стоимости 0, как показано на рис. 6.25. Назовем новый “дополненный граф” G'.
(6.29) Дополненный граф G' содержит такой отрицательный цикл C, что существует путь из C в конечную точку t в том и только в том случае, если исходный граф содержит отрицательный цикл.
Доказательство. Предположим, G содержит отрицательный цикл. Тогда цикл C очевидно содержит ребро к t в G', поскольку все узлы содержат ребро к t.
Теперь предположим, что G' содержит отрицательный цикл с путем к t. Так как никакое ребро не выходит из t в G', этот цикл не может содержать t. А поскольку G' совпадает с G во всем, кроме узла t, этот цикл также является отрицательным циклом в G. ■
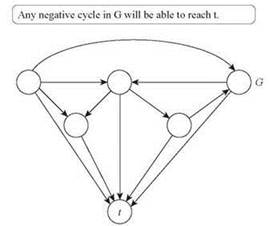
Рис. 6.25. Дополненный граф
Итак, для решения задачи достаточно определить, содержит ли G отрицательный цикл с путем к заданному конечному узлу t; этим мы сейчас и займемся.
Разработка и анализ алгоритма
Наша работа над алгоритмом начнется с адаптации исходной версии алгоритма Беллмана-Форда, которая была менее эффективной в использовании памяти. Начнем с расширения определений OPT(i, v) из алгоритма Беллмана-Форда, определив их для значений i ≥ n. При наличии в графе отрицательного цикла (6.22) уже не действует, и кратчайший путь может становиться все короче и короче при многократном проходе отрицательного цикла. Для любого узла v в отрицательном цикле, у которого имеется путь к t, действует следующее утверждение:
(6.30) Если узел v может достигнуть узла t и входит в отрицательный цикл, то
![]()
Если граф не содержит отрицательных циклов, то из (6.22) вытекает следующее утверждение:
(6.31) Если G не содержит отрицательных циклов, то OPT(i, v) = OPT(n - 1, v) для всех узлов v и всех i ≥ n.
Но для насколько больших значений i нужно вычислить значения OPT(i, v), прежде чем сделать вывод об отсутствии в графе отрицательных циклов? Например, узел v может удовлетворять уравнению OPT(n, v) = OPT(n - 1, v) и при этом все равно лежать на отрицательном цикле. (А вы видите почему?) Как выясняется, гарантии дает только выполнение условия для всех узлов.
(6.32) В графе не существует отрицательного цикла с путем к узлу t в том и только в том случае, если OPT(n, v) = OPT(n - 1, v) для всех узлов v.
Доказательство. Утверждение (6.31) уже доказано в прямом направлении. Что касается обратного направления, мы воспользуемся аргументом, примененным ранее для обоснования безопасности преждевременной остановки алгоритма Беллмана-Форда. А именно, предположим, что OPT(n, v) = OPT(n - 1, v) для всех узлов v. Значения OPT(n + 1, v) могут быть вычислены по OPT(n, v); но все эти значения совпадают с соответствующими OPT(n - 1, v). Следовательно, выполняется равенство OPT(n + 1, v) = OPT(n - 1, v). Распространяя эти рассуждения на будущие итерации, мы видим, что ни одно из значений никогда не изменится снова, то есть OPT(i, v) = OPT(n - 1, v) для всех узлов v и всех i ≥ n. Следовательно, не может быть отрицательного цикла C, имеющего путь к t; для любого узла w в этом цикле C из (6.30) следует, что значения OPT(i, w) становятся сколь угодно отрицательными с увеличением i. ■
Утверждение (6.32) предоставляет механизм O(mn) для принятия решения о том, существует ли в G отрицательный цикл, способный достичь t. Мы вычисляем значения OPT(i, v) для узлов G и для значений i вплоть до n. Согласно (6.32), отрицательного цикла не существует в том, и только в том случае, если существует некоторое значение i < n, для которого OPT(i, v) = OPT(i - 1, v) для всех узлов v.
Итак, мы определили, имеется ли в графе отрицательный цикл с путем из цикла к t, но сам цикл еще не найден. Чтобы найти отрицательный цикл, рассмотрим такой узел v, что OPT(n, v) = OPT(n - 1, v): для этого узла путь P из v в t со стоимостью OPT(n, v) должен использовать ровно n ребер. Этот путь минимальной стоимости P из v в t находится обратным отслеживанием по подзадачам. Как и в доказательстве (6.22), простой путь может содержать только n-1 ребер, поэтому путь P должен содержать цикл C. Утверждается, что цикл C имеет отрицательную стоимость.
(6.33) Если граф G состоит из n узлов и OPT(n, v) = OPT(n - 1, v), то путь P из v в t стоимостью OPT(n, v) содержит цикл C и C имеет отрицательную стоимость.
Доказательство. Сначала заметим, что путь P должен содержать n ребер, так как OPT(n, v) = OPT(n - 1, v), поэтому каждый путь, содержащий n - 1 ребер, имеет стоимость большую, чем у пути P. В графе с n узлами путь, состоящий из n ребер, должен содержать (хотя бы) повторяющийся узел; пусть w — узел, встречающий в P более одного раза. Пусть C — цикл в P между двумя последовательными вхождениям узла w. Если бы цикл C не был отрицательным, то удаление C из P дало бы путь v-t, содержащий менее n ребер и имеющий не большую стоимость. Это противоречит нашему предположению о том, что OPT(n, v) = OPT(n - 1, v), а следовательно, цикл C должен быть отрицательным. ■
(6.34) Описанный выше алгоритм находит отрицательный цикл в G, если такой цикл существует, и выполняется за время O(mn).
Расширения: улучшенные алгоритмы нахождения кратчайшего пути и отрицательного цикла
В конце раздела 6.8 рассматривалась реализация алгоритма Беллмана-Форда, эффективная по затратам памяти, для графов, не содержащих отрицательных циклов. В этом разделе мы реализуем обнаружение отрицательных циклов способом, не менее эффективным в отношении затрат памяти. Помимо экономии памяти, он также значительно ускоряет работу алгоритма даже для графов без отрицательных циклов. Реализация будет базироваться на том же графе указателей P, построенном из “первых ребер” (v, first[v]), который использовался в реализации из раздела 6.8. Согласно (6.27) мы знаем, что если граф указателей содержит цикл, то этот цикл имеет отрицательную стоимость, и работа на этом завершается. Но если G содержит отрицательный цикл, гарантирует ли это, что граф указателей будет содержать цикл? Кроме того, сколько лишнего вычислительного времени уйдет на периодические проверки наличия цикла в P?
В идеале нам хотелось бы определять, появляется ли цикл в графе указателей при каждом добавлении нового ребра (v, w) с first[v] = w. Дополнительное преимущество такого “моментального” обнаружения циклов заключается в том, что нам не придется ожидать n итераций, чтобы узнать, содержит ли граф отрицательный цикл: алгоритм может завершиться сразу же после обнаружения отрицательного цикла. Ранее было показано, что если граф G не содержит отрицательных циклов, алгоритм может быть остановлен на ранней стадии, если при какой-то итерации значения кратчайшего пути M[v] остаются неизменными для всех узлов v. Моментальное обнаружение отрицательного цикла станет аналогичным правилом раннего завершения для графов, содержащих отрицательные циклы.
Рассмотрим новое ребро (v, w) с first[v] = w, добавленное в граф указателей P. Перед добавлением (v, w) граф указателей не содержит циклов, поэтому он состоит из путей от каждого узла v к конечной точке t. Наиболее естественный способ проверки того, приведет ли добавление ребра (v, w) к созданию цикла в P, заключается в отслеживании текущего пути от w к t за время, пропорциональное длине этого пути. Если на этом пути будет обнаружен узел v, значит, образовался цикл и, согласно (6.27), граф содержит отрицательный цикл. Пример представлен на рис. 6.26, где указатель first[v] обновляется с и на w; в части а это не приводит к появлению (отрицательного) цикла, а в части b приводит. Однако при таком отслеживании серии указателей от vможно потратить время до O(n), если дойти по пути до t, так и не обнаружив цикла. Сейчас мы рассмотрим метод, не требующий увеличения время выполнения на O(n).
Мы знаем, что перед добавлением нового ребра (v, w) граф указателей был направленным деревом. Другой способ проверки того, приводит ли добавление (v, w) к созданию цикла, основан на рассмотрении всех узлов поддерева, направленного к v. Если w входит в это поддерево, то (v, w) образует цикл; в противном случае этого не происходит. (И снова рассмотрите два примера на рис. 6.26.) Чтобы найти все узлы в поддереве, направленном к v, в каждом узле v необходимо хранить список всех остальных узлов, ребра которых указывают на v. С такими указателями поддерево можно найти за время, пропорциональное размеру поддерева, указывающего на v, — снова максимум O(n). Однако на этот раз нам удастся извлечь дополнительную пользу из уже проделанной работы. Обратите внимание на то, что текущее значение расстояния М[х] для всех узлов х в поддереве было вычислено на основании старого значения узла v. Мы только что обновили расстояние узла v, а следовательно, знаем, что расстояния всех этих узлов будут обновлены снова. Пометим каждый из этих узлов x как “пассивный”, удалим ребро (x, first[x]) из графа указателей и не будем использовать x для будущих обновлений, пока не изменится его значение расстояния.
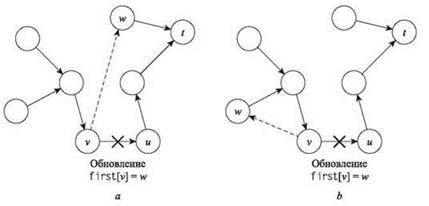
Рис. 6.26. Изменение графа указателей P при обновлении first[v] с и на w. На рис. b это приводит к появлению (отрицательного) цикла, а на рис. a — нет
Такие изменения могут сэкономить немало работы при обновлениях, но как это отразится на времени выполнения в худшем случае? Пометка пассивных узлов после каждого обновления расстояний может потребовать дополнительного времени до O(n). Однако узел может быть помечен как пассивный только в том случае, если в прошлом для него был определен указатель, поэтому затраты времени на пометку пассивных узлов не превышают время, потраченное алгоритмом на обновление расстояний.
А теперь рассмотрим время, проводимое алгоритмом за другими операциями, кроме пометки пассивных узлов. Вспомните, что алгоритм разбит на итерации, а итерация i + 1 обрабатывает узлы, расстояние которых было обновлено на итерации i. Для исходной версии алгоритма в (6.26) мы показали, что после i итераций значение M[v] не превышает значение кратчайшего пути из v в t, использующего не более i ребер. Однако при большом количестве пассивных узлов на каждой итерации это может быть не так. Например, если кратчайший путь из v в t, использующий максимум i ребер, начинается с ребра e = (v, w) и узел w пассивен в этой итерации, обновить значение расстояния M[v] не удастся, а значит, останется значение, превышающее длину пути через ребро (v, w). Казалось бы, возникает проблема, однако в данном случае путь через ребро (v, w) не является кратчайшим, поэтому у M[v] позднее будет возможность обновиться еще меньшим значением.
Итак, вместо простого свойства, действовавшего для M[v] в исходных версиях алгоритма, мы имеем следующее утверждение:
(6.35) Во время работы алгоритма M[v] — длина некоторого простого пути из v в t; путь содержит не менее i ребер, если значение расстояния M[v] обновляется на итерации i; после i итераций значение M[v] представляет длину кратчайшего пути для всех узлов v, для которых существует кратчайший путь v-t, содержащий не более i ребер.
Доказательство. Указатели first образуют дерево путей к t, из чего следует, что все пути, используемые для обновления расстояний, являются простыми. Тот факт, что обновления на итерации iпорождаются путями, содержащими не менее i ребер, легко доказывается индукцией по i. Аналогичным образом индукция используется для доказательства того, что после итерации i значение M[v] представляет расстояние для всех узлов v, для которых кратчайший путь из v в t содержит не более i ребер. Обратите внимание: узлы v, для которых M[v] содержит фактическое расстояние кратчайшего пути, не могут быть пассивными, так как значение M[v] будет обновлено при следующей итерации для всех пассивных узлов. ■
Используя это утверждение, мы видим, что время выполнения алгоритма в худшем случае по-прежнему ограничивается O(mn): время, потраченное на пометку пассивных узлов, игнорируем; каждая итерация реализуется за время O(m), и может быть не более n - 1 итераций, обновляющих значения в массиве M без нахождения отрицательного цикла, так как простые пути могут содержать не более n - 1 ребер. Наконец, время, потраченное на пометку пассивных узлов, ограничивается временем, потраченным на обновления. Обсуждение завершается следующим утверждением относительно быстродействия алгоритма в худшем случае: как упоминалось ранее, эта новая версия на практике оказывается самой быстрой реализацией алгоритма для графов, не содержащих отрицательных циклов, и даже ребер с отрицательной стоимостью.
(6.36) Усовершенствованная версия алгоритма, описанная выше, находит отрицательный цикл в G, если такой цикл существует. Она завершается немедленно, если граф указателей P из указателейfirst[v] содержит цикл C или существует итерация, при которой никакие значения расстояний M[ v] не изменяются. Алгоритм использует память O(n), выполняется за максимум nитераций и за время O(mn) в худшем случае.