Алгоритмы - Разработка и применение - 2016 год
Эпилог: алгоритмы, которые работают бесконечно
У каждого десятилетия свои увлекательные головоломки; и если в начале 1980-х годов бесспорное первое место среди математических развлечений занимал кубик Рубика, то “Тетрис” вызывает похожее чувство ностальгии по концу 80-х и началу 90-х годов. У кубика Рубика и “Тетриса” есть кое-что общее: математический оттенок, базирующийся на стилизованных геометрических формах, — но пожалуй, различия между ними представляют еще больший интерес.
Кубик Рубика — игра, сложность которой определяется огромным пространством поиска; к заданной перемешанной конфигурации кубика требуется применить серию операций, чтобы достичь конечной цели. С другой стороны, “Тетрис” (в его “чистой” форме) имеет куда более размытое определение успеха; вместо конкретной конечной точки вы сталкиваетесь с бесконечным потоком событий, на которые необходимо непрерывно реагировать.
Эти отличительные признаки “Тетриса” напоминают аналогичные темы, проявившиеся в недавних работах по анализу алгоритмов. Все чаще встречаются ситуации, в которых традиционные представления об алгоритмах — в начале выполнения алгоритм получает входные данные, выполняется за конечное количество шагов и выдает результат — уже неприменимы. Попробуйте представить себе маршрутизаторы в Интернете, которые передают пакеты и пытаются избежать перегрузок; или децентрализованные механизмы обмена файлами, которые копируют и распространяют контент по требованию пользователей; или средства машинного обучения, формирующие прогностические модели концепций, изменяющихся со временем; во всех этих случаях мы имеем дело с алгоритмами, практически предназначенными для бесконечного выполнения. Признаком успешного выполнения является не окончательный результат, а способность алгоритма сохранить работоспособность в постоянно изменяющейся среде, постоянно подкидывающей новые задачи. В таких ситуациях мы переходим из мира кубика Рубика в мир “Тетриса”.
Существует много разных примеров, на которых можно исследовать эту тему. В последнем разделе книги мы рассмотрим одну из самых интересных ситуаций: разработку алгоритмов для высокоскоростной коммутации пакетов в Интернете.
Задача
Пакет, перемещающийся от источника к получателю в Интернете, можно представить как маршрут обхода пути в большом графе, узлам которого соответствуют сетевые коммутаторы, а ребрам — кабели, которые связывают коммутаторы. У каждого пакета p имеется заголовок, по которому коммутатор при поступлении пакета p по входному каналу может определить выходной канал, через который p следует отправить. Таким образом, задача сетевого коммутатора — взять поток пакетов, прибывающих по входным каналам, и как можно быстрее переместить каждый пакет в конкретный выходной канал, по которому он должен быть отправлен. Насколько быстро? В средах с высокой нагрузкой пакет может поступать на каждый входной канал через несколько десятков наносекунд; если пакеты не будут передаваться на соответствующие выходные каналы со сравнимой скоростью, то трафик начнет накапливаться, что приведет к потере пакетов.
Чтобы рассуждать об алгоритмах, работающих внутри коммутатора, мы определим модель коммутатора следующим образом: он имеет n входных каналов I1, ..., In и n выходных каналов O1, ..., On. Пакеты прибывают по входным каналам; с пакетом p связывается тип ввода/вывода (I[p], O[p]), который указывает, что он поступил по входному каналу I[p] и должен отправиться по выходному каналу O[p]. В системе ведется дискретный отсчет времени; за один шаг на каждом входном канале прибывает не более одного нового пакета и не более одного пакета может отправиться по каждому выходному каналу.
Рассмотрим пример на рис. Е.1. За один квант времени на пустой коммутатор прибывают три пакета p, q и r по входным каналам I1, I3 и I4 соответственно. Пакет p предназначен для выходного канала O1, пакет q — для канала O3, и пакет r тоже предназначен для O3. С отправкой пакета по каналу O1 проблем нет; но по каналу O3 может быть отправлен только один пакет, поэтому коммутатор должен разрешить конфликт между q и r. Как это сделать?
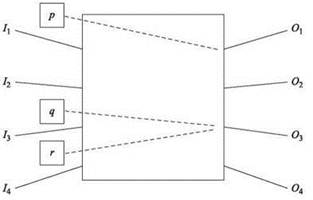
Рис. E.1. Коммутатор с n = 4 входными и выходными каналами. За один временной шаг прибывают пакеты p, q и r
Простейшее поведение коммутатора в такой ситуации называется чистой выходной очередью; по сути, это идеализированная картина того, что бы мы хотели видеть от коммутатора. В этой модели все пакеты, прибывающие на некотором шаге, помещаются в выходной буфер, связанный с выходным каналом, и отправляется один из пакетов из каждого выходного буфера. Ниже приведена более конкретная модель одного временного шага.

Итак, на рис. E.1 заданный временной шаг может закончиться тем, что пакеты p и q будут отправлены по своим выходным каналам, а пакет r останется в выходном буфере O3. (В дальнейшем обсуждении этого примера предполагается, что при принятии решений q отдается предпочтение перед r.) В этой модели коммутатор представляется как идеальный объект, через который пакеты беспрепятственно проходят к своему выходному буферу.
Однако на практике пакет, поступивший по входному каналу, необходимо скопировать в соответствующий выходной канал, а эта операция требует некоторых вычислений, которые блокируют входной и выходной каналы на несколько наносекунд. Итак, в действительности ограничения коммутатора создают некоторые препятствия при перемещении пакетов из входных каналов в выходные.
Самая жесткая модель этих ограничений — очереди ввода/вывода — работает следующим образом: имеется входной буфер для каждого входного канала I, а также выходной буфер для каждого выходного канала O. При поступлении пакет немедленно помещается в соответствующий входной буфер. За один временной шаг коммутатор может прочитать не более одного пакета из каждого входного буфера и записать не более одного пакета в каждый выходной буфер. Итак, в модели очередей ввода/вывода пример на рис. E.1 будет работать так: каждый из пакетов p, q и r помещается в отдельный входной буфер; коммутатор перемещает p и q в их выходные буферы, но не может переместить все три пакета, потому что для этого пришлось бы записать два пакета в выходной буфер O3. Таким образом, первый шаг завершится отправкой пакетов p и q по их выходным каналам, а пакет r остается во входном буфере I4 (вместо выходного буфера O3).
На более общем уровне ограничение на количество операций чтения и записи выглядит так: если пакеты p1, ..., pl перемещаются за один временной шаг из входных буферов в выходные, то все их входные и выходные буферы должны быть различны. Другими словами, типы {(I[pi], O[pi]): i = 1, 2, ..., l} должны образовать двудольное паросочетание. Тогда один временной шаг можно смоделировать следующим образом.

Выбор перемещаемого паросочетания пока остается не определенным; важность этого момента станет ясна позднее.
Итак, при использовании очередей ввода/вывода коммутатор создает некоторое “трение” на пути перемещения пакетов, причем это объективно наблюдаемое явление: если рассматривать коммутатор как “черный ящик” и просто наблюдать за последовательностью отправок по выходным каналам, можно заметить различия между чистой выходной очередью и очередями ввода/вывода. Рассмотрим пример, в котором первый шаг в точности повторяет рис. Е.1, а на втором шаге прибывает один пакет s типа (I4, O4). При использовании чистой выходной очереди пакеты pи q отправятся на первом шаге, а r и s — на втором. С другой стороны, при использовании очередей ввода/вывода происходит последовательность событий, изображенная на рис. Е.2: в конце первого шага r по-прежнему находится во входном буфере I4, а в конце второго шага один из пакетов r или s также остается во входном буфере I4, ожидая отправки. Конфликт между r и sназывается блокировкой очереди; из-за него коммутатор с очередями ввода/вывода по своим характеристикам задержки уступает чистой выходной очереди.
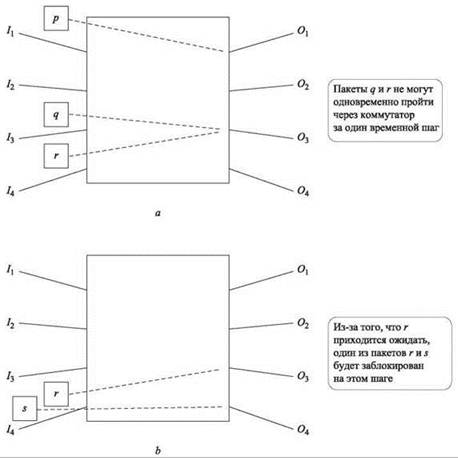
Рис. E.2. Двухшаговый процесс, приводящий к блокировке очереди
Моделирование чистой выходной очереди
Поведение чистой выходной очереди было бы удобным, но из сказанного выше понятно, что препятствует реализации коммутатора с таким поведением: за один временной шаг (продолжительностью всего десятки наносекунд) переместить пакеты из одного из n входных каналов в общий выходной буфер в общем случае не удастся.
Но что, если взять коммутатор с очередями ввода/вывода и ускорить его работу, перемещая несколько сочетаний за шаг вместо одного? Возможно ли смоделировать коммутатор, использующий чистую выходную очередь? Под этим термином здесь понимается, что последовательность отправок по выходным каналам (при которой коммутатор рассматривается как “черный ящик”) должна быть одинаковой для реализации поведения чистой выходной очереди и ускоренного алгоритма очередей ввода/вывода.
Нетрудно понять, что ускорения в n раз будет достаточно: если мы сможем перемещать n сочетаний на каждом шаге, то даже если все прибывающие пакеты должны попасть в один выходной буфер, мы смогли бы переместить их все за один шаг. Но ускорение в n раз совершенно нереально; и если рассматривать происходящее как худший случай, появляется неприятная мысль о том, что без ускорения в n раз не обойтись, — в конце концов, что делать, если все прибывающие пакеты действительно должны быть направлены в один выходной буфер?
В этом разделе будет показано, что хватит гораздо более умеренного ускорения. Мы опишем поразительный результат, который получили Чуан, Гоэл, Маккеун и Прабхакар (Chuang, Goel, McKeown, Prabhakar, 1999), — он показывает, что коммутатор, использующий очереди ввода/вывода с ускорением 2, может моделировать коммутатор с чистой выходной очередью. На уровне здравого смысла этот результат использует тот факт, что внутреннее поведение коммутатора не обязано напоминать поведение чистой выходной очереди, если последовательность отправок пакетов с выходных каналов остается неизменной. (Следовательно, продолжая пример из предыдущего абзаца, не обязательно перемещать все n входных пакетов в общий выходной буфер за один шаг; для этого можно выделить больше времени, потому что их отправки по общему выходному каналу все равно будут распределены по более длинному периоду времени.)
Разработка алгоритма
Просто для ясности приведем модель для ускорения 2.

Чтобы доказать, что эта модель способна имитировать чистую выходную очередь, необходимо разрешить важный, недостаточно определенный момент: какие паросочетания должны перемещаться на каждом шаге? Ответ на этот вопрос образует основу результата, и мы придем к нему через серию промежуточных шагов. Начнем с одного простого наблюдения: если пакет типа (I, O) является частью паросочетания, выбранного коммутатором, то коммутатор переместит пакет этого типа с самым ранним временем отправки.
Организация входных и выходных буферов
Чтобы решить, какие два паросочетания коммутатор должен переместить на заданном шаге, необходимо определить некоторые характеристики, определяющие текущее состояние коммутатора относительно чистой выходной очереди. Для начала для пакета p определяется его время отправки TL(p), равное временному шагу, на котором он был бы отправлен по выходному каналу коммутатора при использовании чистой выходной очереди. Мы стремимся к тому, чтобы каждый пакет p отправлялся из коммутатора (с ускоренными очередями ввода/вывода) ровно на шаге TL(p).
На концептуальном уровне каждый входной буфер представляет собой упорядоченный список; при этом сохраняется возможность вставки прибывающих пакетов в середину порядка, а также перемещения пакета в выходной буфер даже тогда, когда он еще не находится в начале очереди. Несмотря на это, линейное упорядочение буфера образует полезную метрику прогресса. С другой стороны, выходные буферы упорядочивать не нужно; когда приходит время отправки пакета, он просто покидает буфер. Конфигурация напоминает терминал аэропорта: входные буферы соответствуют стойкам регистрации, выходные — залам ожидания, а внутренняя реализация коммутатора — сильно загруженному контрольному пункту службы безопасности. Основное напряжение приходится на входные буферы: если не успеть к началу очереди до завершения регистрации, то вы можете опоздать на самолет; к счастью, служащие аэропорта могут извлечь вас из середины очереди и провести через контрольный пункт в ускоренном темпе. Напротив, в выходных буферах можно расслабиться: пассажиры спокойно сидят, пока не будет объявлена посадка на их рейс, после чего просто отправляются на самолет. Главное — преодолеть “затор” в середине, чтобы пассажиры успели к отлету.
В частности, из этой аналогии следует, что нам не нужно беспокоиться о пакетах, уже находящихся в выходных буферах; они отправятся в нужное время. Соответственно мы будем называть пакет p необработанным, если он все еще находится во входном буфере, и определим некоторые полезные метрики для таких пакетов. Входным окномIC(p) называется количество пакетов, находящихся перед пакетом p в его входном буфере. Выходным окномOC(p) называется количество пакетов, уже находящихся в выходном буфере p и имеющих более раннее время отправки. У необработанного пакетаp дела идут хорошо, если OC(p) намного больше IC(p); в этом случае p находится ближе к началу очереди в его входном буфере, а в выходном буфере перед ним еще остается много пакетов. Для представления этой связи мы определим метрику Slack(p) = OC(p) - IC(p), заметив, что большие значения Slack(p) являются предпочтительными.
Итак, наш план: паросочетания будут передаваться по коммутатору так, чтобы постоянно сохранялись следующие два свойства:
(i) Slack(p) ≥ 0 для всех необработанных пакетов р;
(ii) На любом шаге, начинающемся с IC(p) = OC(p) = 0, пакет p будет перемещаться в свой выходной буфер в первом паросочетании.
Сначала нужно убедиться в том, что сохранения этих двух свойств достаточно.
(E.1) Если свойства (i) и (ii) выполняются для всех необработанных пакетов во все моменты времени, то каждый пакет p будет отправлен в свое положенное время TL(p).
Доказательство. Если p находится в своем выходном буфере в начале шага TL(p), то, очевидно, он может быть отправлен; в противном случае он бы находился во входном буфере. В таком случае OC(p) = 0 в начале шага. Согласно свойству (i), имеем Slack(p) = OC(p) - IC(p) ≥ 0, а следовательно, IC(p) = 0. Затем из свойства (ii) следует, что пакет p будет перемещен в выходной буфер в первом паросочетании этого шага, а следовательно, также будет отправлен в этом шаге. ■
Как выясняется, свойство (ii) гарантируется достаточно легко (и оно естественно выполняется в приведенном ниже решении), поэтому мы сосредоточимся на непростой задаче выбора паросочетаний для поддержания свойства (i).
Перемещение паросочетания через коммутатор
Когда пакет p только прибывает во входной канал, он вставляется как можно ближе к концу входного буфера (вероятно, где-то в середине) в соответствии с требованием Slack(p) ≥ 0. Это гарантирует, что свойство (i) будет изначально выполняться для p.
Чтобы поддерживать неотрицательность Slack с течением времени, необходимо побеспокоиться о компенсации событий, приводящих к убыванию Slack(p). Вернемся к описанию одного временного шага и подумаем, как происходит такое убывание.

Рассмотрим пакет p, остающийся необработанным в начале временного шага. В фазе прибытия IC(p) может увеличиться на 1, если прибывающий пакет помещается во входной буфер передp. Это приведет к уменьшению Slack(p) на 1. В фазе отправки этого шага OC(p) может уменьшиться на 1, так как пакет с более ранним временем отправки уже не будет находиться в выходном буфере. Это тоже приведет к уменьшению Slack(p) на 1. Итак, Slack(p) теоретически может уменьшиться на 1 в каждой из фаз прибытия и отправки. Соответственно выполнение свойства (i) будет обеспечено, если мы сможем гарантировать, что Slack(p) увеличивается по меньшей мере на 1 при каждом перемещении паросочетания через коммутатор. Как этого добиться?
Если перемещаемое паросочетание включает пакет из I[p], находящийся перед р, то IС(р) уменьшается, а следовательно, Slack(p) увеличится. Если паросочетание включает пакет, предназначенный для O[p], но имеющий более раннее время отправки, чем р, то OC(p) и Slack(p) возрастут. Итак, проблема возникает только в том случае, если не происходит ни одно из этих событий. На рис. E.3 приведено схематичное изображение такой ситуации. Предположим, пакет x перемещается из I[р] даже в том случае, если он находится ближе к концу очереди, а пакет у перемещается в O[p], хотя он имеет более позднее время отправки. В такой ситуации буферы I[p] и O[p] работают “некорректно”: для I[p] было бы лучше отправить пакет, находящийся ближе к началу очереди (такой, как p), а для O[p] было бы лучше получить пакет с более ранним временем отправки (такой, как p). В сочетании два буфера образуют некий аналог неустойчивости из задачи об устойчивом паросочетании.
Мы можем этот принцип выразить точно — и он станет ключом для завершения алгоритма. Допустим, для выходного буфера O входной буфер I является предпочтительным перед /', если самое раннее время отправки среди пакетов типа (I, O) меньше самого раннего времени отправки между пакетами типа (I', O). (Иначе говоря, если у буфера I существует более срочная потребность отправить что-то в буфер O.) Кроме того, для входного буфера I выходной буфер O является предпочтительным перед выходным буфером O', если ближайший к началу пакет типа (I, O) опережает ближайший к началу пакет типа (I, O') в упорядочении I. Для каждого буфера по этим правилам строится список предпочтений; и если пакетов типа (I, O) вообще нет, то I и Oпомещаются в конец списка предпочтений друг друга, с произвольной разбивкой связей. Наконец, алгоритм определяет устойчивое паросочетание M с учетом этих списков предпочтений, и коммутатор перемещает это паросочетание M.
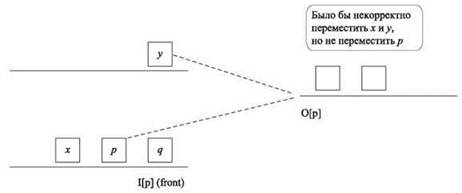
Рис. E.3. Выбор перемещаемого паросочетания
Анализ алгоритма
Следующее утверждение показывает, что выбор устойчивого паросочетания действительно дает алгоритм с нужными гарантиями быстродействия.
(E.2) Предположим, коммутатор всегда перемещает устойчивое паросочетание M в отношении списков предпочтений, определенных выше. (И для каждого типа (I, O), содержащегося в M, выбирается пакет этого типа с самым ранним временем отправки.) Тогда для всех необработанных пакетов p при перемещении паросочетания M значение Slack(p) увеличивается минимум на 1.
Доказательство. Рассмотрим любой необработанный пакет р. Продолжая предшествующее обсуждение, предположим, что в составе паросочетания M не перемещается никакой пакет, опережающий р в I[p], и никакой пакет, предназначенный для O[p], с более ранним временем отправки. Итак, пара (I[p], O[p]) не принадлежит M; предположим, что пары (I', O[p]) и (I[p], O') принадлежат M.
Пакет p имеет более раннее время отправки, чем любой пакет типа (I', O[p]), и опережает все пакеты типа (I[p], O') в упорядочении I[p]. Отсюда следует, что для I[p] буфер O[p] является предпочтительным перед O', и для O[p] буфер I[p] является предпочтительным перед I'. Следовательно, пара (I[p], O[p]) образует неустойчивость, что противоречит предположению об устойчивости M. ■
Следовательно, перемещая устойчивое паросочетание на каждом шаге, коммутатор поддерживает свойство Slack(p) ≥ 0 для всех пакетов p; следовательно, в соответствии с (E.1) мы доказали следующее:
(E.3) Перемещая два устойчивых паросочетания на каждом временном шаге, в соответствии с только что определенными предпочтениями, коммутатор может имитировать поведение чистой выходной очереди.
Получается, алгоритм совершенно неожиданно встречается в теме, с которой начиналась книга, — но вместо пар из мужчин и женщин или работодателей и работников здесь формируются пары входных и выходных каналов в высокопроизводительном интернет-маршрутизаторе.
Мы всего лишь мельком затронули тему алгоритмов, работающих бесконечно в условиях бесконечного потока новых событий. В этой интересной области полно нерешенных проблем и открытых направлений. Но этой темой мы займемся как-нибудь в другой раз и в другой книге, а эта книга подошла к концу.